II_prova__Settembre_2006

Cognome e nome:
A.A. 2005/2006
Fisica I (Meccatronica)
II APPELLO SETTEMBRE (28/9/2006)
Luogo e data di nascita
Matricola
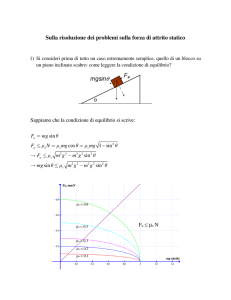
1. Un blocco di massa M = 10 kg è fermo su un piano inclinato con  = 60° sotto l’azione della forza peso,
della forza di attrito statico (coefficiente di attrito blocco-piano S = 0.2) e di una forza F applicata
orizzontalmente. Calcolare: (a) il valore minimo del modulo di F affinché il blocco non scivoli in basso; (b) il
valore massimo del modulo di F affinché il blocco non cominci a muoversi verso l’alto.
M
F

2 Un punto materiale di massa m = 10 kg scivola partendo da fermo sotto l’azione della forza peso lungo un
piano inclinato con  = 60° rispetto all’orizzontale per una lunghezza L = 1 m. Alla fine del piano inclinato il
punto materiale va ad incastrarsi (urto completamente anelastico) dentro un blocco di massa M = 100 kg in
quiete su un piano orizzontale con coefficiente di attrito dinamico d = 0.5. Calcolare lo spazio percorso sul
piano dopo l’urto dal sistema blocco + punto materiale prima di arrestarsi.
m
L
M
d
3. Una sfera piena di raggio R = 20 cm e massa M = 1 kg viene poggiata in quiete alla sommità di un piano
inclinato scabro di inclinazione  = 30° a una quota h = 50 cm dal piano orizzontale. Calcolare: (a) il valore
minimo del coefficiente di attrito statico con il piano perché la sfera rotoli senza strisciare sotto l’azione della
forza peso; (b) la velocità angolare della sfera quando raggiunge il piano orizzontale.
M
h

QUESITI (oltre alle formule necessarie MAX 30 parole ognuno)
A) Scrivere le equazioni della cinematica di un moto unidimensionale.
B) Scrivere le equazioni delle componenti normale e tangenziale di un moto piano.
C) Cosa si intende per forze conservative?
D) Scrivere l’espressione del Teorema di Konig per l’energia cinetica di sistema di punti materiali specificando il significato
dei termini.
E) Quale è la definizione e le caratteristiche di un asse principale di inerzia?
SOLUZIONI ESERCIZI
1)
dall’equazione vettoriale per l’equilibrio statico:


 
F  mg  FA  R N  0
proiettata sulla tangente e sulla normale al piano, otteniamo:
caso a)
Fcos  mgsen   FA  0
Fsen  mgcos   R N  0
con
FA  μS R N  μS (Fsen  mgcos  )
otteniamo
Fcos  mgsen   μS (Fsen  mgcos  )  0 
FMIN  mg
caso b)
sen  μS cos 
cos  μS sen 
 111.8 N
Fcos  mgsen   FA  0
Fsen  mgcos   R N  0
sempre con
Fcos  mgsen   μS (Fsen  mgcos  )  0 
FMIN  mg
2)
sen  μS cos 
cos  μS sen 
Fcos  μS sen   mg sen  μS cos 
FA  μS R N  μS (Fsen  mgcos  )
Fcos  μS sen   mg sen  μS cos 
 230.2 N
alla fine del piano inclinato per la conservazione dell’energia il punto materiale avrà una
velocità:
v 
2 gLsen
per la conservazione della quantità di moto nell’urto anelastico la velocità del blocco subito
dopo l’urto sarà:
V
m
v
Mm
per il teorema del lavoro (della forza di attrito) e dell'energia cinetica:

1
1  m
T  MV 2  M
v 
2
2  M  m 
2
 s(M  m)gD
quindi:
s  M
m2
Lsen  13  10-3 m
 D M  m 3
Per garantire il puro rotolamento, ovvero l’equilibrio statico del punto di contatto, la forza
di attrito dovrà eguagliare la componente tangenziale al piano della forza peso:
3)
FA  Mg sen   S R N   S Mg cos
da cui:
 S  tg  0.58
per la conservazione dell'energia meccanica e considerando il puro rotolamento:
1 2
12
1
1
7
mv 
mR2 2  m 2 R 2  mR2 2 
mR2 2  mgh
2
25
2
5
10

10
gh
7
 13.24 rad/s
R
da cui :