Maturità 2008 – Sessione Straordinaria.
Problema 1.
Sia data la parabola di equazione y ax 2 bx c
1. Si determini a,b,c in modo che la parabola passi per il punto A(0,-6), B(1,0) e nel punto B
sia tangente alla retta di coefficiente angolare 5.
2. Si determinino le misure dei lati del rettangolo di perimetro massimo inscritto nel segmento
parabolico limitato dalla parabola e dall’assex
3. Trovato questo rettangolo ed essendo M ed N i due suoi vertici che stanno sulla parabola, si
calcoli in gradi e primi (sessagesimali) l’ampiezza dell’angolo acuto formato dalle due
tangenti alla parabola in M ed N.
1.
y ax 2 bx c y ' 2ax b . Imponendo il passaggio per A e B e imponendo in B la derivata
uguale a 5. (per significato geometrico della derivata)
6 c
0 c
c 6
7 25
2
0 a b c b a 6
b 7 y x 7 x 6 V ;
2 4
5 2a b
5 2a a 6 a 1
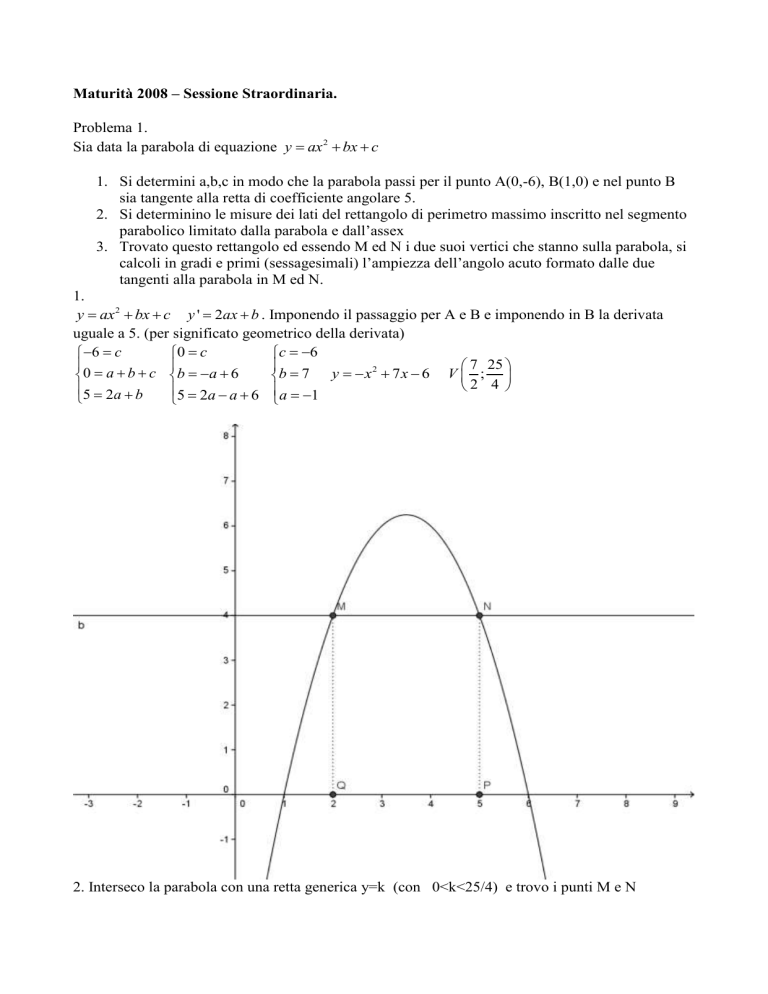
2. Interseco la parabola con una retta generica y=k (con 0<k<25/4) e trovo i punti M e N
y x2 7 x 6
y k
7 25 4k
x2 7 x 6 k 0
x
M,N
2
y k
y k
7 25 4k
7 25 4k 7 25 4k
7 25 4k
M
; k N
; k Q
; k P
; k
2
2
2
2
MN xN xM
MQ k 0 k
7 25 4k 7 25 4k 2 25 4k
25 4k
2
2
2
Da cui Perimetro( MNPQ) 2( MN MQ) 2(k 25 4k )
Perimetro massimo per
Perimetro(k ) ' 2(1
25 4k 2 0
4
25 4k 2
)2
0 la cui espressione è positiva per
2 25 4k
25 4k
25 4k 2
25 4k 2 25 4k 4 4k 21 k
21
4
(Valore massimo)
21
21
21
21
29
.
Perimetro( ) 2( 25 4 ) 2( 2)
4
4
4
4
2
Osserviamo che agli estremi ho valori inferiori al massimo.
25
25
25
25 25
Perimetro(0) 2(0 25 0) 2(5) 10 Perimetro( ) 2( 25 4 )
4
4
4
2
9
5 21
9 21
3. per il valore massimo ho M ; N ;
2 4
2 4
m ' m
1 m m '
Dove m e m’ sono i coefficienti angolari della retta tangente nel punto N ed M
L’angolo si calcola con la formula tan
5
m 2axM b 2 7 2
2
22 4
1 4 3
Problema 2
9
m ' 2axN b 2 7 2
2
4
3
arc tan 53,13
tan
53(13 60) ' 538'
x 1
x2 2
1. Si studi tale funzione e si tracci il grafico , su un piano riferito ad un sistema di assi
cartesiani ortogonali (Oxy).
2. Si scriva l’equazione della tangente alla curva nel punto d’intersezione con l’asse y.
Si consideri la funzione
f ( x) ln
3. Si studi la funzione g ( x) e f ( x ) e se ne tracci il grafico .
1.
f ( x) ln
x 1
x2 2
f ( x) ln
x 1
0
x2 2
lim ln
x 1
C.E.
x 1
0
x2 2
x 1
1
x2 2
x 1
x=-1 A.V.
x2 2
x 1
f ( x) ln 2
x 2
x 0
x 1
( x 2 x 2)
x2 x 2
0 mai positiva e nulla
0
x2 2
x2 2
lim ln
x
x 1
ln 0 x=-1 A.V.
x2 2
1
f (0) ln ln 2 0, 69
Non ha intersezione con l’asse x.
2
x 0
1 ( x 2 2) (2 x)( x 1) x 2 2 x 2 2 2 x 2 2 x x 2 2 x 2 2 x 2
f '( x)
x 1
( x 2 2)2
x 1
( x 2 2) 2
x 1 ( x 2 2) 2
2
x 2
f '( x)
x 2 2 ( x 2 2 x 2) ( x 2 2 x 2)
0 1 3 x 1 3
x 1 ( x 2 2)2
( x 1)( x 2 2)
x 2 2 x 2 0 x 1 1 2 1 3
1 3
1 3
x 1 3 min. (non sta nel campo di esistenza)
x 1 3
Tralasciamo lo studio della derivata seconda e facciamo lo studio della derivata prima agli estremi.
( x 2 2 x 2)
lim
0 all’infinito non va con valori bassi poco pendente ( e questo significa che ha
x ( x 1)( x 2 2)
un flesso dopo il massimo)
Vista la difficoltà di studiare la derivata seconda potrei passare direttamente al grafico, e saltare il
calcolo della derivata seconda. (Il calcolo che segue si può saltare.)..
A partire dalla derivata prima scritta come segue, calcolo la derivata seconda.
x2 2 x 2
f '( x) 3
x x2 2x 2
(2 x 2)( x3 x 2 2 x 2) (3x 2 2 x 2)( x 2 2 x 2)
f ''( x)
x3 x 2 2 x 2
2 x 4 2 x3 4 x 2 4 x 2 x3 2 x 2 4 x 4 (3x 4 6 x3 6 x 2 2 x3 4 x 2 4 x 2 x 2 4 x 4)
f ''( x)
x3 x 2 2 x 2
f ''( x)
2 x 4 4 x3 6 x 2 8 x 4 (3x 4 8 x3 4)
x3 x 2 2 x 2
2 x 4 4 x3 6 x 2 8 x 4 3x 4 8 x3 4 x 4 4 x3 6 x 2 8 x 8
x3 x 2 2 x 2
x3 x 2 2 x 2
Applico Ruffini al polinomio p( x) x 4 4 x3 6 x 2 8x 8
f ''( x)
Provo per 1, 2, 4, 8
p(1) 1 4 6 8 8 17
p(1) 1 4 6 8 8 9
p(2) 16 32 24 16 8 0
p( x) ( x 2)( x3 6 x 2 6 x 4)
Nel secondo polinomio devo applicare Ruffini 1, 2, 4 e provando no trovo soluzioni razionali.
Ora dovrei studiare la funzione q( x) ( x3 6 x 2 6 x 4) , per trovare le soluzione, (con il metodo di
approssimazione. Non riporto risultati. La soluzione è x 4,95 tale soluzione. Sta oltre il C.E.
Quindi ho un unico flesso, per x=2
1
2. Tangente nel punto (0; ln 2) (0;ln )
2
y f ( x0 ) f '( x0 )( x x0 )
f (0) ln
1
2
3. f ( x) e
f ( x)
lim
x
ln
f '(0)
x 1
x2 2
x 1
0
x2 2
2
1
2
y ln
1
1
1( x 0) y x ln x ln 2
2
2
x 1
C.E. (1; )
x2 2
x 1
x 1
0 y=0 A.O.
x2 2
Intersezione asse x A(-1,0)
Intersezione asse y B(0,1/2)
f '( x)
( x 2 2) ( x 1)(2 x) x 2 2 x 2
1 3 x 1 3
( x 2 2)2
( x 2 2)2
( x 2 2)2 (2 x 2) 2( x 2 2)(2 x)( x 2 2 x 2)
f ''( x)
( x 2 2)2
2 x3 2 x 2 4 x 4 4 x 4 8x 2 8x
x 3 3x 2 6 x 2
2
f ''( x) ( x 2 2)
2(
x
2)
0 ….
( x 2 2)2
( x 2 2)2
Occorre discuterla con il calcolo approssimato…
2. Si determinino le equazioni degli asintoti della curva f ( x) arctan x
C.E. (; ) non ha asintoti verticali.
lim arctan x
x
3.
x
0 da cui
2
1 x
2
y
2
x
1 x2
A. O. (destro e sinitro)
Un cilindro dentro un cono visto in sezione appare come
in figura. Il volume di un cilindro si trova V Abase h FH 2CH
Quindi occorre trovare il raggio e l’altezza del cilindro pongo raggio FH x con 0 x r
CH HA
L’altezza del cilindro KH h y ricordandoci le proporzioni abbiamo che
ovvero
CK HF
x
h
rh hx
h r
cioè h h da cui KH h x
r
r
r
y x
rh hx h 2
h 2 3
x (r x)
rx x derivando
r
r
r
h
2
V '( x)
2rx 3 x 2 0 da cui massimo per x r
r
3
V ( x) Abase h x 2
8 3 h 4 3 4
2
2
r r r
r hr
r 9
27 r 27 27
4x2
3x
,x 0
4. Si consideri la funzione f ( x)
x
2
x0
Se ne studi la funzione e poi si tracci il grafico
Vmax
h 4
2| x|
,x 0
3 x
f ( x)
x
2
x0
3 x 2, x 0
f ( x ) 3 x 2, x 0
2
x0
3x 2, x 0
a sinistra e a destra ho due funzioni continue (polinomio di primo grado).
f ( x)
3x 2, x 0
Studio la continuità in 0. lim f ( x) 2 lim f ( x) 2 la funzione in 0 non è continua.
x 0
x 0
5.
f ( x) sin 2 x
f ( x h) f ( x )
sin 2 ( x h) sin 2 ( x)
(sin x cosh cos x sinh) 2 sin 2 ( x)
lim
lim
h 0
h 0
h 0
h
h
h
2
2
2
2
2
sin x cos h cos x sin h 2sin x cos x sinh cosh sin ( x)
lim
h 0
h
2
2
2
2
sin x(1 cos h) cos x sin h 2sin x cos x sinh cosh
lim
h 0
h
f '( x) lim
(1 cos 2 h)
sin 2 h
sinh
cos 2 x
2sin x cos x
cosh
h 0
h
h
h
sinh cosh
lim 0 0 2sin x cos x
2sin x cos x
h 0
h
6. la proposizione è falsa
limsin 2 x
Perché basta se prendo due rette r e s , con
Con angolo _ rs rs 90 . Questo è un esempio che contraddice la proposizione
0 x
La funzione f(x) non è continua in
. E quindi non derivabile.
2
1
1 cos3 x
Anche se f (0) 0 f ( ) 0 f '( x)
cos
x
0 cos3 x 1 x , l’unico
2
2
cos x
cos x
punto in cui si annulla nell’intervallo, ma tale punto non è interno. E quindi non esiste il punto a
derivata nulla all’interno dell’intervallo.
x 2 2 x x 4 0
8. y ln( x 2 2 x x 4)
2
x 2 x 0
7.
f ( x) tan x sin x
x2 2 x x 4
x2 2 x 0 x 4 0
2
2
x 4 0
x 2 x ( x 4)
x 0 x 2 x 4
2
2
x 4
x 2 x x 8x 16
x 0 x 2 x 4
x 4
6 x 16 0
x 0 2 x 4 x 4
Da cui C.E. x 0 x 2
esin x cos x
0
cos xesin x sin x 1 0
lim
1
x 0 e cos x e log( x e)
0 x0 sin xecos x e
0 1
xe
10. lim










