scheda_7 - Liceo Morgagni

Scheda 7: IL TEOREMA DEI SENI
1.
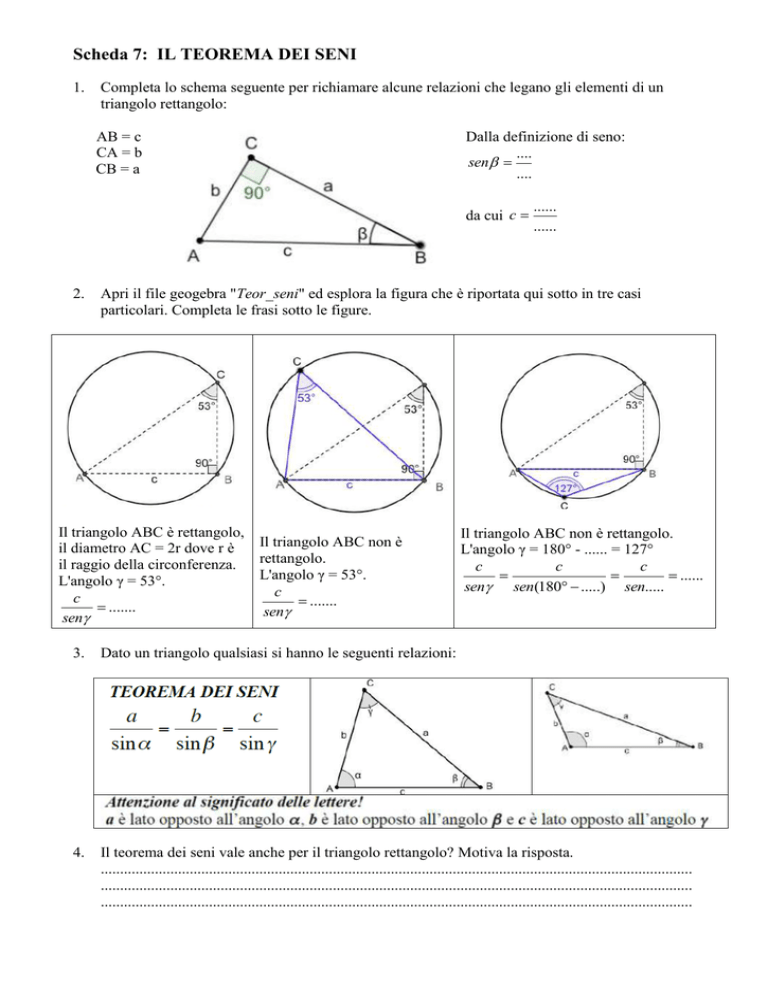
Completa lo schema seguente per richiamare alcune relazioni che legano gli elementi di un
triangolo rettangolo:
AB = c
CA = b
CB = a
Dalla definizione di seno:
....
sen 
....
da cui c 
2.
......
......
Apri il file geogebra "Teor_seni" ed esplora la figura che è riportata qui sotto in tre casi
particolari. Completa le frasi sotto le figure.
Il triangolo ABC è rettangolo,
Il triangolo ABC non è
il diametro AC = 2r dove r è
rettangolo.
il raggio della circonferenza.
L'angolo γ = 53°.
L'angolo γ = 53°.
c
c
 .......
 .......
sen
sen
Il triangolo ABC non è rettangolo.
L'angolo γ = 180° - ...... = 127°
c
c
c


 ......
sen sen(180  .....) sen.....
3.
Dato un triangolo qualsiasi si hanno le seguenti relazioni:
4.
Il teorema dei seni vale anche per il triangolo rettangolo? Motiva la risposta.
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
5.
Completa le seguenti frasi riferite alla figura a fianco:
................ è una corda della circonferenza
................ è un angolo alla circonferenza
................ è un angolo alla circonferenza che
insiste sulla corda .......
............... è un triangolo inscritto nella
circonferenza
La circonferenza è circoscritta al triangolo ......
6.
Completa il seguente enunciato del teorema dei seni:
"In un qualunque triangolo, il rapporto fra ........... e il seno dell'angolo ........... è uguale al
diametro della .............................."
7.
Facendo riferimento alla figura dell'esercizio 5, il segmento AC è sia lato del triangolo ABC sia
corda della circonferenza. Applicando il teorema dei seni a tale triangolo possiamo enunciare il
seguente teorema della corda:
"Una corda di una circonferenza è data dal prodotto del ............. della circonferenza per il seno
di un qualunque angolo ................. che ............. sulla ...................."
8.
Riprendiamo il problema iniziale della nave in difficoltà.
Del triangolo rettangolo ABC, che non è rettangolo, conosco tutti gli angoli in quanto risulta
γ = 180° - ........................ = .......
a
400
b


Per calcolare i lati applico il teorema dei seni scritto nella forma:
sen....... sen..... sen....
da cui trovo a = ............. e b = ..............
9.
Completa lo schema seguente per riassumere tutte le relazioni fra lati e angoli di un triangolo.
In figura a, b e c indicano le lunghezze dei lati e α, β e γ le ampiezze degli angoli.
10. Completa il seguente procedimento per risolvere un triangolo ABC di cui sono dati: β = 34°,
c = 7 e a = 20.
Per calcolare b applico il teorema del
coseno,
da cui b = ..............
Per calcolare α applico il teorema del
coseno,
da cui α = ...............
Per calcolare γ sfrutto la somma degli angoli
interni,
da cui γ = ...............