Scaletta

Scaletta per studiare l’interazione
radiazione-materia
• Cominciare con ‘perturbazione armonica’, che
tratta la teoria generale della perturbazione armonica,
cioè sviluppa i conti della teoria delle perturbazioni
dipendenti dal tempo, nel caso di perturbazione che
oscilla nel tempo armonicamente.
Qui c’è la discussione del famoso ‘diffraction
pattern’, nonché della regola aurea di Fermi.
• proseguire con ‘teoria perturbativa (I)’, che
introduce le grandezze necessarie all’applicazione
della teoria delle perturbazioni allo studio
dell’interazione tra un’onda elettromagnetica e un
atomo.
Si ottiene uno sviluppo in serie di multipoli
dell’elemento di matrice della perturbazione.
In particolare si arriva al cosiddetto «termine di
dipolo elettrico dell’elemento di matrice della
perturbazione» in funzione dell’operatore
(operatore di posizione lungo l’asse z, che è l’asse
del dipolo).
** a questo punto la sequenza logica si biforca : da
una parte si può
• proseguire con le ‘regole di selezione’, che
forniscono dei criteri per stabilire tra quali coppie di
stati elettronici è possibile una transizione
(probabilità di transizione apprezzabilmente non
nulla)
** oppure si può
• passare alla ‘teoria perturbativa (II)’ che, a partire
dall’espressione dell’elemento di matrice del termine
di dipolo della perturbazione, espresso in funzione
del campo elettrico e dell’operatore di perturbazione,
sviluppa i conti applicando la teoria generale della
perturbazione armonica, per ottenere una probabilità
di transizione.
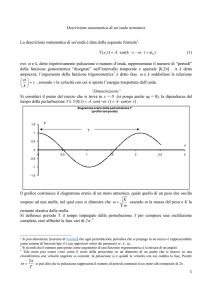
In particolare si considera dapprima un’onda
monocromatica, e poi il caso più realistico di
pacchetto d’onda, e si perviene ad un’espressione
della probabilità di transizione in funzione sia del
campo elettrico medio, sia dell’intensità dell’onda,
che della densità di energia (che sono tre grandezze
facilmente legate le une alle altre).
• Si passa poi a studiare la teoria fenomenologica di
Einstein.
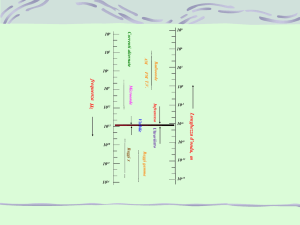
Dapprima, con un metodo grafico, si calcola la
densità di modi di oscillazione di una radiazione
elettromagnetica all’interno di una cavità conduttrice
(densità sia rispetto al volume che rispetto alla
frequenza).
In seguito, con un approccio a cavallo tra la teoria
elettromagnetica classica e la teoria quantistica
(fotoni) si passa alla densità di energia in funzione
della frequenza.
Poi, richiamando l’espressione della probabilità di
transizione in funzione della densità di energia
trovata prima (teoria perturbativa (II)), in essa si
sostituisce l’espressione della densità di energia.
Alla fine, con considerazioni fenomenologiche si
riesce a descrivere (ma non a giustificare) anche il
fenomeno dell’emissione spontanea