PERTURBAZIONE ARMONICA

PERTURBAZIONE ARMONICA
Consideriamo un potenziale perturbativo armonico nel tempo V'(x,t)=V 1(x)exp(it). La conoscenza esplicita della
dipendenza dal tempo ci consente di fare un passo avanti, rispetto al caso generale di un sistema quantistico qualsiasi,
soggetto ad un potenziale perturbativo non altrimenti specificato. In particolare, nella definizione dei coefficienti (v.
capitolo sulla Matrice di Transizione)
c k t   
t
i
V' kn e iknt ' dt' , con V' kn   k x , V' n x 
 0
(si noterà che ci siamo messi nel caso semplice in cui lo stato di partenza è dato da una sola
autofunzione che evolve verso la "mistura"
x, t    n x e
i
En
t

x, t    c k t  k x e

i
Ek
t

k
t0
t  0)
possiamo cercare di definire dapprima l'elemento di matrice V'kn, che deve essere una funzione del tempo, e poi
calcolare esplicitamente l'integrale temporale sopra indicato.
Tuttavia si pone un porblema: l'operatore V'=V1(x)exp(it), ottenuto "copiando" l'espressione del potenziale
perturbativo non è hermitiano, come si vede verificando direttamente che è diverso dal suo complesso coniugato.
Possiamo ovviare a questo problema definendo come operatore:
V (x)e it  V1* (x)e it
V'  1
2
Questa espressione, come si può facilmente verificare, è hermitiana.
Ecco allora che nel calcolo di V'kn si ottiene:
V' kn   k ,
V1 (x)e it  V1* (x)e it
1
1
 n   k , V1 (x) n e it   k , V1* (x) n e it
2
2
2
Non è difficile vedere come i due prodotti scalari siano due numeri complessi coniugati. Definendo quindi
U kn   k , V1 ( x ) n
U kn*   k , V1* ( x ) n
possiamo scrivere
1
1
U kn e it  U kn *e it
2
2
Non possiamo dire nulla di più sugli U kn, ma possiamo proseguire nel calcolo di ck(t):
V' kn 
t
c k t   

t
i
V' kn e iknt ' dt' 
0

t


0
0
t
2i
t
U kn e i kn t ' dt'  U kn * e i kn t ' dt'
U kn e it ' e iknt ' dt'  U kn * e it ' e iknt ' dt'



0
0
2i

1 
e i kn t  1
e i kn t  1 
 U kn *
 U kn

2 
 kn  
 kn   
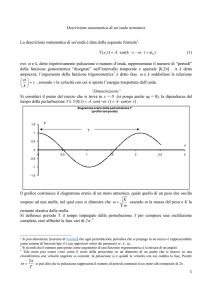
Il risultato ottenuto dice che, essendo gli U kn proporzionali al piccolo potenziale V1(x), ed essendo i moltiplicatori delle
frazioni con il numeratore oscillante in modulo tra 0 e 2 ed il denominatore in generale diverso da zero, allora i
coefficienti ck(t) (che inizialmente sono nulli per tutti i kn) rimangono piccolissimi, ossia non vi sono in generale
transizioni.
Tuttavia per alcuni valori particolari della pulsazione  della perturbazione il denominatore di una delle due frazioni
può diventare molto piccolo, portando l'intero valore di c k(t) a valori elevatissimi, e quindi a grandissime probabilità di
transizione.
Ricordando la definizione di kn tramite la differenza tra la energia del livello iniziale En e quella Ek del generico livello
E  En
di "arrivo" della transizione kn  k
, osserviamo che mentre la pulsazione del potenziale V' è definita positiva

(non ha senso una pulsazione negativa), la "pulsazione" kn può avere entrambi i segni: dipende solo dalla "altezza"
relativa tra le energie En e Ek.
Questo fatto dice una cosa assai importante: se è vero che per E k>En il denominatore che si può annullare è quello con
kn-, indicando una transizione da energie basse ad energie alte, che si può immaginare avvenire a spese
(assorbimento) di parte della energia della perturbazione, è altrettanto vero che per E k<En può annullarsi altrettanto bene
il denominatore kn+, essendo kn0. In questo caso la transizione alto-basso prevede la espulsione (emissione) di
una quantità di energia pari al "dislivello" En-Ek, ossia E  E n  E k  kn . Se questa espulsione avviene mediante
l'emissione di una particella a cui sia associabile tramite la relazione di Planck una pulsazione , si vede come la
particella espulsa abbia la stessa pulsazione della perturbazione incidente. Vedremo come nel caso di perturbazione da
onda elettromagnetica, la pulsazione del potenziale sia quella associata ad un flusso di fotoni incidenti, e come la
espulsione di energia da parte del sistema corrisponda alla emissione di un fotone aggiuntivo a quelli della
perturbazione.
E', questo, il fenomeno della emissione stimolata, ipotizzato per primo da Einstein agli inizi del '900.
Per rendere più evidente questa possibilità di avere sia transizioni basso-alto che alto-basso, osserviamo come, per
quanto si è detto, l'espressione dei ck(t) sia o piccolissima, oppure sia grande per merito o dell'uno o dell'altro dei due
termini indicati a secondo membro, e quando l'uno è grandissimo, l'altro è sicuramente piccolissimo. Si può dunque
scrivere, limitandoci alla espressione del modulo quadro di ck(t):
c k t  
2
1
2
U kn
4 2
e i kn t  1
 kn  
2
Qui il segno  ha significato esclusivo: o vale il +, o vale il -.
Elaboriamo brevemente questa espressione, osservando che:
e i kn t  1 
2
       kn   
i  kn
t
t
 i
e 2  e 2 



   
i  kn
t
e  2 
2


 


  kn  
     i 2  t
i  kn

t e 
2ie  2  



   
i  kn
t
e  2 
2i
2


  4 sen 2   kn   t 

2




per cui
c k t  
2
1
2
U kn
2
  
sen 2  kn
t
2

 1 U
kn
2
4 2
kn  
2
  
sen 2  kn
t
2


 kn   


2


2
sen 2 (at )

 2 a  dapprima moltiplichiamo e dividiamo il secondo membro
t 
a 2t
per t, e poi eseguiamo questo limite per l'ultima frazione:
  
  
sen 2  kn
t
sen 2  kn
t
2
2
1
1
2
2
2



  2 U 2 t kn    .
c k t   2 U kn
 2 U kn t


kn
2
2
t 
2


2


  kn   
 kn   



 t
2
2




Se infine ricordiamo la proprietà della delta:
1   kn   
1

x   x  per cui
  2 kn    2E k  E n  
 
2


abbiamo:
4
2
2
c k t  
U kn t  E k  E n  

Sfruttando ora il limite notevole
Il senso di c k t 
2
torna chiaro quando si ricordi (cap. matrice di Transizione) come la norma della funzione d'onda di
un sistema costituita da una "mistura" di funzioni di base ortonormalizzate sia N 2   c k N 2 k   c k
2
k
2
: il
k
modulo quadro dei coefficienti c k t  dà la probabilità (che si evolve nel tempo) di avere una particella nello specifico
2
stato k-esimo. Dividendo questa probabilità per il tempo t, si ottiene la probabilità di transizione dal livello iniziale n al
livello k nell'unità di tempo, ossia, quello che per definizione è il tasso di transizione da n a k:
Wn k 
c k t 2
t

4
2
U kn E k  E n  

Prima di commentare questo risultato, sgombriamo il campo da un possibile legittimo dubbio: come è possibile da un
lato ipotizzare (v. Matrice di Transizione) c k t   
t
t
i
i
 c n t'V'kn eiknt 'dt'     c n  V'kn eiknt 'dt' , usando la
 n 0
n
0
approssimazione di tempi t abbastanza piccoli da considerare il sistema talmente poco modificato da approssimare i
cn(t) con i loro valori iniziali costanti cn, e poi fare il limite per t grandissimo, in modo da ottenere l'espressione limite
della delta? La risposta è che le due cose non sono incompatibili. Possiamo infatti considerare che tempi corrispondenti
a molti periodi (T=2/) siano grandi a sufficienza per giustificare il limite della delta, ma piccoli abbastanza da
considerare il sistema "appena perturbato".
Il commento importante, ora, è vedere come la perturbazione armonica induca una ferrea regola di selezione, che
impone una relazione tra le energie E k, En dei livelli coinvolti nelle transizioni e la pulsazione  (energia  ) della
perturbazione stessa:
  E k  E n
Il modulo sulla differenza indica come la medesima perturbazione possa causare transizioni con guadagno o con
dispendio di energia da parte del sistema. Nel primo caso si parlerà di assorbimento, nel secondo caso di emissione
stimolata di energia da parte del sistema stesso.
La regola di selezione indica le transizioni possibili, ma riserva ad un passo successivo la definizione di quelle che
effettivamente avverranno: rimane infatti l'elemento di matrice di transizione U kn che può indicare la probabilità
relativa tra le transizioni possibili, che può anche essere nulla (transizioni proibite).
PERTURBAZIONE DA UN'ONDA ELETTROMAGNETICA PIANA
Il caso di gran lunga più interessante, per questo corso, di perturbazione armonica è quello di un'onda elettromagnetica
piana. Il problema è come associare a questa onda un potenziale perturbativo utilizzabile nella nostra teoria fin qui
sviluppata.
Il problema principale è che noi introduciamo la perturbazione come un potenziale scalare aggiuntivo V' alla equazione
della energia totale
p2
 V  V'
2m
mentre dalle equazioni di Maxwell il campo elettromagnetico è associato ai potenziali  e A che non sono solo scalari:

1 A
E   
c t

B   A
E
Qui dobbiamo chiedere soccorso alla teoria dei Campi Elettromagnetici, che dice come l'energia di una particella di
massa m immersa in un potenziale scalare ordinario V ed anche in un campo elettromagnetico, descritto dal potenziale
elettrostatico  e dal potenziale vettore A, sia data dalla espressione:
2
e 

p  A
c 
E
 e  V
2m
dove e è la carica elementare e c la velocità della luce.
Accettando questa espressione senza dimostrazione, si constata tuttavia come questa risolva il problema, rendendo
scalari tutti i termini a secondo membro, che può essere esplicitato sviluppando il quadrato (prodotto scalare):

 p2
  1  e  2
e
E
 V  
A  p
 A   e 
mc

 2m
  2m  c 
Si riconoscerà nel termine in parentesi quadra il termine consueto per l'energia cinetica e l'energia potenziale, mentre
nella parentesi graffa sono radunati tutti i termini che coinvolgono il campo elettromagnetico.
Se ora consideriamo un'onda elettromagnetica sufficientemente debole da essere considerata una perturbazione di un
sistema materiale, da un lato escludiamo la presenza di un campo elettrostatico, per cui =0, e dall'altro lato ipotizziamo
che eA/c sia molto piccolo rispetto ai valori della quantità di moto p della particella. Questo significa che della parentesi
graffa, il termine di gran lunga più significativo, ancorchè piccolo, se confrontato con l'energia cinetica e potenziale del
sistema, sia l'ultimo, dove entra il prodotto (scalare) tra il potenziale vettore A che la quantità di moto p.
Scrivendo allora
  p 2
 p2
  1  e  2
 e
e
E
 V  
A  p  
 V 
A p
 A   e 
mc
  2m
 2m
  2m  c 
 mc
riconosciamo subito il ruolo di potenziale perturbativo alla grandezza fisica
e
V'  
Ap
mc
La evidente importanza della direzione dei vettori nel calcolo del prodotto scalare ci sconsiglia dal limitarci al caso
unidimensionale, dove si può scrivere V'=V'(x,t), suggerendo invece la formulazione V'=V'(x,y,z,t)=V'(r,t).
Per giungere al nostro caso di interesse, l'onda piana elettromagnetica, consideriamo un potenziale elettrostatico nullo
=0 ed il seguente potenziale vettore:
Ar, t   xˆ A 0 exp i k opt  r  t


dove A0 è semplicemente una costante (eventualmente complessa), e l'esponenziale ha l'andamento di un'onda piana
descritta nello spazio tridimensionale dal suo vettore d'onda kopt e dalla sua pulsazione . Il suffisso "opt" serve a
distinguere questo vettore d'onda, relativo alla radiazione elettromagnetica, e le sue componenti k x opt, ky opt, kz opt dai
vettori d'onda k relativi alle onde di Schroedinger (ricordiamo che per una particella libera, la funzione d'onda è proprio
un'onda piana), ossia alle onde materiali.
La scelta di un potenziale vettore diretto lungo la specifica direzione x non è limitante: si può pensare di aver adeguato
il sistema di riferimento, per comodità di calcolo, alla direzione constatata per il vettore A.
Prima di vedere come questa espressione porta alla scrittura di un operatore di perturbazione, verifichiamo se a questa
corrisponda, in termini di campo elettromagnetico, un'onda piana. Caratteristica di questa è che tutte le componenti del
campo elettrico e del campo magnetico siano armoniche nello spazio e nel tempo, e che i vettori campo elettrico e
campo magnetico risultino ortogonali. La prova è immediata già dalle definizioni di E e B, in assenza di potenziale
elettrostatico e con la definizione di A data. Tuttavia, a livello di esercizio, osserviamo come

1 A
1 A

E   

 i xˆ A 0 exp i k opt  r  t
c t
c t
c

xˆ

x

B    A  A 0 e it
e
ik optr
yˆ

y
0

zˆ
  e ik optr

 A 0 e it yˆ 
z
  z
0


  iA exp i k  r  t yˆ k
ˆ k yopt
0
opt
z opt  z


  e ik optr
  zˆ 
  y
 


e come si nota. il termine esponenziale, che rappresenta l'oscillazione nello spazio e nel tempo, è comune a tutte le
componenti, mentre E e B risultano ortogonali (B giace nel piano yz, mentre E è diretto lungo la direzione x).
Con questa espressione di A, il potenziale perturbativo diventa:
e
V'  
A 0 exp i k opt  r  t  p x
mc
Nel momento in cui trasformiamo questa grandezza fisica in un operatore, dobbiamo ricordarci di renderlo hermitiano,
scrivendo:
ie 

ie 

V' 
A 0 exp i k opt  r  t 

A 0 * exp  i k opt  r  t 

2mc
x 2mc
x


 ie 
 ie 
 e it 
A 0 exp ik opt  r    e it 
A 0 * exp  ik opt  r  
2
mc

x
2
mc

x



dove nell'ultima espressione si sono poste in evidenza le dipendenze armoniche. I termini tra parentesi quadra svolgono
qui il ruolo dei termini Ukn della trattazione generale sulla perturbazione armonica.
Ricordando il risultato fondamentale di quella trattazione
4
2
2
c k t  
U kn t  E k  E n  

si potrà quindi scrivere direttamente l'espressione
e

U kn 
A 0  k , exp  ik opt  r 
n
mc
x





 






Rimane solo da ricordare che qui, dove la trattazione si ferma perché ogni ulteriore passo in avanti richiede la
conoscenza delle funzioni d'onda, la coppia di queste che compare nel prodotto scalare conserva gli indici k ed n (che in
tre dimensioni avrebbero una espressione molto più complessa) per indicare come queste siano autofunzioni diverse
del medesimo operatore hamiltoniano imperturbato, ossia soluzioni diverse del medesimo problema di Schroedinger
indipendente dal tempo.