Descrizione matematica di un’onda armonica
La descrizione matematica di un’onda è data dalla seguente formula1:
Y ( x; t ) = A ⋅ cos(k ⋅ x − ω ⋅ t + ϕ 0 )
(1)
ove ω e k, dette rispettivamente pulsazione e numero d’onda, rappresentano il numero di “periodi”
della funzione goniometrica “disegnati” nell’intervallo temporale e spaziale [0,2π] . A è detta
ampiezza; l’argomento della funzione trigonometrica2 è detto fase. ω e k soddisfano la relazione
⎛ω ⎞
⎜ ⎟ = v , essendo v la velocità con cui si sposta l’energia trasportata dall’onda.
⎝k⎠
“Dimostrazione”
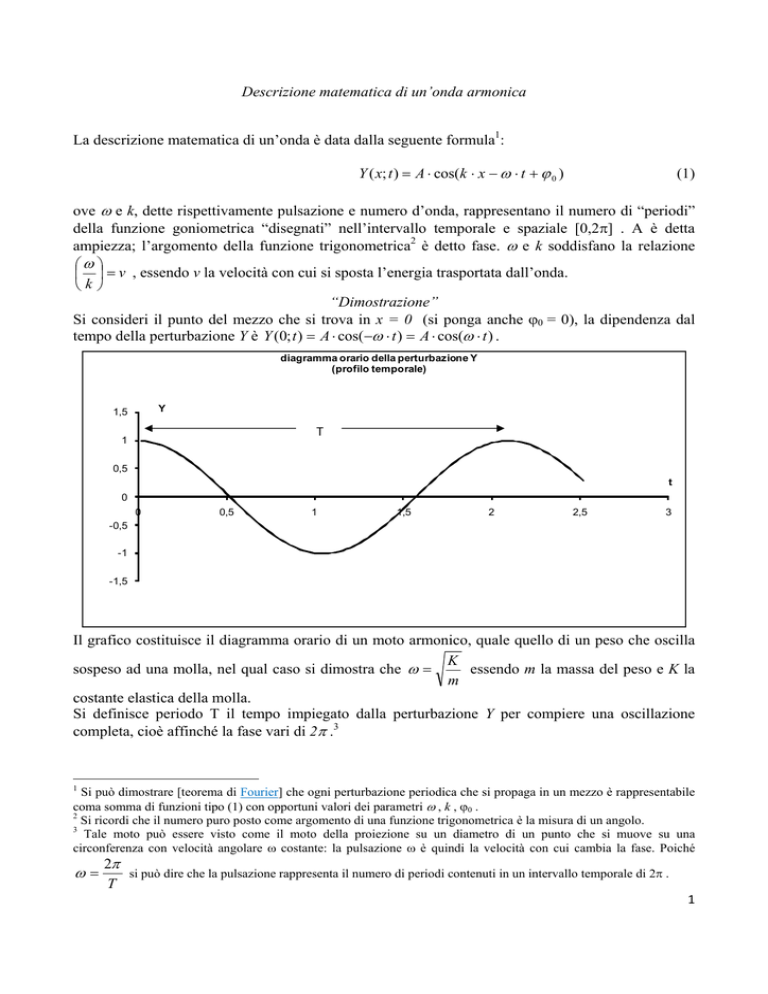
Si consideri il punto del mezzo che si trova in x = 0 (si ponga anche ϕ0 = 0), la dipendenza dal
tempo della perturbazione Y è Y (0; t ) = A ⋅ cos(−ω ⋅ t ) = A ⋅ cos(ω ⋅ t ) .
diagramma orario della perturbazione Y
(profilo temporale)
Y
1,5
T
1
0,5
t
0
0
0,5
1
1,5
2
2,5
3
-0,5
-1
-1,5
Il grafico costituisce il diagramma orario di un moto armonico, quale quello di un peso che oscilla
K
essendo m la massa del peso e K la
sospeso ad una molla, nel qual caso si dimostra che ω =
m
costante elastica della molla.
Si definisce periodo T il tempo impiegato dalla perturbazione Y per compiere una oscillazione
completa, cioè affinché la fase vari di 2π .3
1
Si può dimostrare [teorema di Fourier] che ogni perturbazione periodica che si propaga in un mezzo è rappresentabile
coma somma di funzioni tipo (1) con opportuni valori dei parametri ω , k , ϕ0 .
2
Si ricordi che il numero puro posto come argomento di una funzione trigonometrica è la misura di un angolo.
3
Tale moto può essere visto come il moto della proiezione su un diametro di un punto che si muove su una
circonferenza con velocità angolare ω costante: la pulsazione ω è quindi la velocità con cui cambia la fase. Poiché
ω=
2π
si può dire che la pulsazione rappresenta il numero di periodi contenuti in un intervallo temporale di 2π .
T
1 Si consideri ora la formula (1) all’istante t = 0 (sempre con
perturbazione Y dalla posizione x è: Y ( x;0) = A ⋅ cos(k ⋅ x) .
ϕ0 = 0); la dipendenza della
Istantanea della perturbazione Y
(profilo spaziale)
Y
1,5
λ
1
0,5
x
0
-2
0
2
4
6
8
10
-0,5
-1
-1,5
Il grafico costituisce il profilo spaziale di un’onda.
Si definisce lunghezza d’onda λ la distanza tra due creste contigue, cioè la distanza che separa punti
sfasati di 2π .4 Più semplicemente si può definire la lunghezza d’onda come la distanza tra due
creste (o valli) consecutive nel profilo spaziale dell’onda.
La collocazione spazio-temporale dell’energia5 che si propaga è stabilita dalla condizione che la
fase α(x,t) = kx - ωt + ϕ0 sia costante.
Facendo riferimento alla soluzione (1), l’energia nella posizione x = 0 e all’istante t = 0 è
rappresentata dal valore della fase α(0,0) = ϕ0 ; all’istante t ≠ 0 tale energia sarà localizzata in una
x ω
posizione x che deve soddisfare l’equazione ϕ0 = kx – ωt + ϕ0 , da cui segue =
. Poiché
t k
ω
x
= V , si ha che
è la velocità con cui si propaga l’energia dell’onda e che viene detta velocità
t
k
dell’onda; risulta infine che v =
ω
k
=
λ
T
= λν , essendo ν la frequenza, cioè il reciproco del periodo.
L’analisi dei grafici sopra fornisce i seguenti dati particolari: A = 1 , T = 2 (dal profilo temporale), λ = 6 (dal profilo
temporale), la cui velocità di propagazione risulta quindi V = 3 . Per determinare la fase iniziale ϕ0 :
ϕ0 = 0
dal profilo temporale in x = 0
⇒
1 = Y (0;0) = 1⋅ cos(ϕ0 ) ⇒
dal profilo spaziale a t = 0
⇒
1 = Y (0;0) = 1⋅ cos(ϕ0 ) ⇒
ϕ0 = 0
4
In maniera analoga a quanto visto nella nota precedente si potrebbe dire che tale legge rappresenta una oscillazione
lungo lo spazio in cui la fase varia proporzionalmente alla variazione di posizione secondo la costante k :
k=
2π
λ
;
dunque il numero d’onda rappresenta il numero di lunghezze d’onda contenute in un intervallo spaziale di 2π .
L’energia associata alla perturbazione è proporzionale ad A2 . Nel caso di un’onda elastica, l’energia, associata
all’oscillazione (moto armonico) dei punti materiali, è la somma dell’energia cinetica ½ mv2 e potenziale elastica ½ kY2,
essendo Y la posizione del punto materiale dal punto di equilibrio e v la velocità del punto materiale. Quando v = 0 si ha
che tutta l’energia è potenziale: ½ k(Ymax)2 e il valore massimo della perturbazione Y si ha proprio quando il valore della
fase è 0 o un multiplo di 2π
5
2 In generale, dalla conoscenza di A, ω, k e del valore della perturbazione in un luogo x ad un istante t : Y(x;t) , si trova il
valore ϕ0 risolvendo l’equazione goniometrica elementare seguente: Y ( x; t ) = A ⋅ cos(k ⋅ x − ω ⋅ t + ϕ 0 ) .
I seguenti grafici rappresentano istantanee dell’onda di equazione:
2π ⎞
⎛ 2π
Y ( x; t ) = 1 ⋅ cos⎜
⋅x−
⋅t ⎟
2 ⎠
⎝ 6
In viola è rappresentata l’istantanea a t = 0
In verde è rappresentata l’istantanea a t = 0,1
In rosso è rappresentata l’istantanea a t = 0,2
3 Sul teorema di Fourier
Il teorema di Fourier afferma che esistono un sacco (!) di funzioni periodiche che possono essere scritte come somma (eventualmente infinita) di funzioni sinusoidali. Quanto segue risulterà più chiaro studiando la matematica del quinto anno (e verrà utilizzato per lo studio della meccanica quantistica). Se la funzione periodica di periodo T è sviluppata come segue: f(x) = A0 + Σ [An cos(nωx) + Bn sin(nωx)] , i coefficienti dello sviluppo di f(x) si calcolano nel seguente modo: T
T
1
A0 = ∫ f ( x ) dx T 0
T
1
An = ∫ f ( x ) cos(nωx ) dx T 0
1
Bn = ∫ f ( x ) sen(nωx ) dx T 0
Se invece si vuole scrivere lo sviluppo seguente: f(x) = A0 + Σ An sin(nωx + ϕn) , allora i coefficienti dello sviluppo di f(x) si calcolano nel seguente modo: 1
posto fn = T
T
∫ f ( x)[ cos(nωx) − i sen(nωx)]dx , è An = 0
⎡ Im( f n ) ⎤
2
f n , ϕ n = arctg⎢
⎥ T
⎣ Re( f n ) ⎦
Di seguito sono presentati i grafici della sviluppo di Fourier (fino a 14 termini) delle funzioni periodiche onda quadra e onda triangolare, i cui sviluppi completi sono: ⎧
⎡ T T⎤
⎪⎪ E ← se − x ∈ ⎢− 4 ; 4 ⎥
⎣
⎦ onda quadra: f (x ) = ⎨
T
T
⎡
⎪0 ← altrove_ in − ; ⎤
⎢⎣ 2 2 ⎥⎦
⎪⎩
con E = π/2 e T = 2π ; f(x) = π
4
∞
+∑
k =1
(− 1)k +1 cos[(2k − 1)x] 2k − 1
N.B. poiché f(0) = E = π/2 ⇒ f(0) = π
4
∞
+∑
k =1
( − 1) k +1
2k − 1
=
π
2
∞
⇒ ∑
k =1
( − 1) k +1
2k − 1
=
π
4
4 5 ⎧2E
⎡ T ⎤
⎪⎪ T x + E ← se − x ∈ ⎢− 2 ;0⎥
⎣
⎦ onda triangolare: f ( x ) = ⎨
E
T
2
⎡
⎤
⎪−
x + E ← se − x ∈ ⎢0; ⎥
⎪⎩ T
⎣ 2⎦
f(x) = π2
8
∞
+∑
k =1
1
( 2 k − 1) 2
N.B. poiché f(0) = E = π2/4 ⇒ f(0) = π2
8
con E = π2/4 e T = 2π ; cos[( 2 k − 1) x ] ∞
+∑
k =1
1
(2 k − 1) 2
=
π2
4
∞
⇒ 1
∑ (2 k − 1)
k =1
2
=
π2
8
6 Confrontando inoltre questo risultato con quello precedente si ha anche che: ∞
∑ (2k − 1)
k =1
⎛ ∞ ( − 1) k +1 ⎞
⎟ = 2 ⎜ ∑
⎝ k =1 2 k − 1 ⎠
2
1
2
Si ricorda che i coefficienti dello sviluppo si ottengono mediante i prodotti scalari nello spazio di Hilbert della funzione periodica da sviluppare con le funzioni del sistema ortonormale completo di Fourier: ∞
f ( x) = A0 + ∑ Ak sen( kx + ϕ k ) k =1
Ak = f ( x) sen(kx Osservazione: si ricordi che le finzioni goniometriche sono sviluppabili in serie di Mc Lorin: x 2 k −1
sen( x) = ∑
k = 1 ( 2 k − 1) !
x 2k
k = 0 2k !
cos( x) = ∑
tan(x) = … Di seguito altri grafici ottenuti con un software di rappresentazione grafica: f(x) = π
4
∞
+∑
k =1
(− 1)k +1 cos[(2k − 1)x] 2k − 1
y=pi/4+cos(x)‐cos(3x)/3+cos(5x)/5‐cos(7x)/7+cos(9x)/9 7 y=pi/4+cos(x)‐cos(3x)/3 f(x) = π2
8
∞
+∑
k =1
1
( 2 k − 1) 2
cos[( 2 k − 1) x ] y=(pi^2)/8+cos(x)+cos(3x)/9+cos(5x)/25+cos(7x)/49+cos(9x)/81+cos(11x)/121+cos(13x)/169 8 y=(pi^2)/8+cos(x)+cos(3x)/9 y=(pi^2)/8+cos(x)+cos(3x)/3 9












