SCUOLA ESTIVA DI MATEMATICA I CICLO
LACENO (AV) 14-16 LUGLIO 2014
CURATO DALLA PROF.SSA EMANUELA SAGNELLA
Da
una valutazione (iniziale, in
itinere, finale), l’insegnante riflette
sui risultati rilevati, affinché possa
programmare nuovi obiettivi,
individuare strategie più efficienti e
rendere più significativo il processo
insegnamento-apprendimento.
POTENZIALITA’
DEGLI ALUNNI
STILI COGNITIVI
DEI RAGAZZI
STRATEGIE
DIDATTICHE ,
METODI,
VALUTAZIONE,
PROGETTAZIONE,
ORGANIZZAZIONE…
MOTIVAZIONE
intrinseca ed
estrinseca
Per
considerare i principali fattori
che influiscono l’apprendimento dei
ragazzi, è opportuno organizzare le
attività didattiche in modo da
creare un ambiente di
apprendimento in cui ciascun
ragazzo sia attivo nel suo percorso
formativo. In tal senso è opportuno
inserire momenti di laboratorio
matematico nelle proprie lezioni.
Come
si legge nelle Indicazioni Nazionali
per il Curricolo, “In matematica, come in
altre discipline scientifiche, è elemento
fondamentale il laboratorio, inteso sia come
luogo fisico sia come momento in cui
l’alunno è attivo, formula le proprie ipotesi
e ne controlla le conseguenze, progetta e
sperimenta, discute e argomenta le proprie
scelte, impara a raccogliere dati e costruisce
significati, porta a conclusioni temporanee e
a nuove aperture la costruzione delle
conoscenze personali e collettive.”
Le
lezioni didattiche devono coinvolgere
ciascun ragazzo e, quindi, essere interattive
con l’intera classe. È necessario proporre
delle situazioni problematiche, per far
scaturire quella motivazione necessaria che
spinge il ragazzo a voler trovare una
soluzione adeguata e, a riflettere sui vari
passaggi per risolvere il problema.
L’insegnante
in questo percorso formativo è
un facilitatore , che guida il ragazzo nei suoi
apprendimenti.
A
partire dai problemi e dagli esempi concreti,
si cerca di estrarre la regola generale e le
formule da poter sperimentare anche in altre
situazioni simili.
Come
si legge nelle Indicazioni Nazionali, la
“caratteristica della pratica matematica è
la risoluzione di problemi, che devono
essere intesi come questioni autentiche e
significative, legate alla vita quotidiana, e
non solo esercizi a carattere ripetitivo o
quesiti ai quali si risponde semplicemente
ricordando una definizione o una regola.”
In
questo laboratorio di matematica è anche
opportuno creare percorsi di insegnamentoapprendimento personalizzati, che tengono conto
delle potenzialità di ogni ragazzo e dei suoi stili
cognitivi.
I quesiti delle Prove Invalsi degli anni scorsi
costituiscono un importante archivio, da cui
l’insegnante può attingere soprattutto per
stimolare i ragazzi a ripassare e ad approfondire i
contenuti appresi. Infatti, come si legge nelle
Indicazioni Nazionali:
“La costruzione del pensiero matematico è un
processo lungo e progressivo nel quale concetti,
abilità, competenze e atteggiamenti vengono
ritrovati, intrecciati, consolidati e sviluppati a
più riprese”
Un
insegnamento - apprendimento diventa
efficace ed efficiente, se c’è continuità
educativa. Non soltanto continuità orizzontale,
che prevede collaborazione con famiglie ed enti
locali, ma anche continuità verticale e ,
nell’Istituto Comprensivo di Gioia, prevede
collaborazione e continuità di obiettivi formativi
a partire dalla Scuola dell’Infanzia fino ad
arrivare alla Scuola Secondaria di I grado.
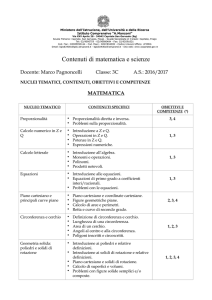
In occasione della continuità verticale, in
matematica , si sta elaborando un curricolo
verticale , su qualche argomento, proposto nei
tre ordini di scuola, sotto forma di didattica
laboratoriale.
Come
•
•
•
•
introdurre il concetto di probabilità:
Lanciare una moneta alcune volte e
registrare la frequenza (assoluta , relativa
percentuale) di testa e croce.
Lanciare la moneta per una cinquantina di
volte e registrare le frequenza di testa e
croce.
Alla fine si confrontano i risultati e si
introduce il concetto di probabilità.
Si approfondisce il concetto di probabilità con altri esempi
pratici della vita quotidiana e con esercizi personalizzati
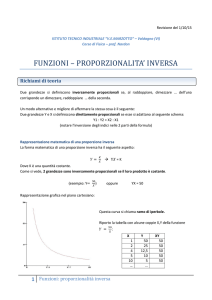
Come introdurre il concetto di proporzionalità
diretta e inversa:
1) Su una carta millimetrata si disegnano diversi
quadrati. Si riportano in una tabella i valori di
ciascun lato e il perimetro. Si riportano i valori
rilevati su un grafico cartesiano (per es. l = x e
P=y). Si guida l’alunno a scoprire che cosa
s’intende per proporzionalità diretta.
2) I ragazzi ritagliano su una carta millimetrata dei
rettangoli equivalenti. Si riportano in una tabella
i valori della base e dell’altezza di ogni
rettangolo. I valori scritti si riportano su un
grafico cartesiano (per es. base= x e altezza=y ).
Si fanno opportune osservazioni sulla
proporzionalità inversa.
•
Si approfondisce il concetto di proporzionalità diretta e inversa
con altri esempi, considerando anche principali leggi scientifiche.
-
Come si può misurare una circonferenza? Esiste
una formula per calcolare la circonferenza
conoscendo il raggio o diametro?
In questo caso i ragazzi con uno spago, trovano
un modo per misurare alcune circonferenze (non
solo disegnate ma anche di oggetti reali).
Dopodiché si misura anche il diametro e si
calcola il rapporto C/d. durante la
socializzazione dei risultati ottenuti, si scopre
che il rapporto C/d è costante e si introduce il
concetto di π e a questo punto gli alunni possono
scoprire la formula per calcolare la
circonferenza.