Revisione del 1/10/15
ISTITUTO TECNICO INDUSTRIALE “V.E.MARZOTTO” – Valdagno (VI)
Corso di Fisica – prof. Nardon
FUNZIONI – PROPORZIONALITA’ INVERSA
Richiami di teoria
Due grandezze si definiscono inversamente proporzionali se, al raddoppiare, dimezzare … dell’una
corrisponde un dimezzare, raddoppiare … della seconda.
Un modo alternativo e migliore di affermare la stessa cosa è il seguente:
Due grandezze Y e X si definiscono direttamente proporzionali se esse si adattano al seguente schema:
Y1 : Y2 = X2 : X1
(notare l’inversione degli indici nelle 2 parti della formula)
Rappresentazione matematica di una proporzione inversa
La forma matematica di una proporzione inversa ha il seguente aspetto:
=K
Dove K è una quantità costante.
Come si vede, 2 grandezze sono inversamente proporzionali se il loro prodotto è costante.
(esempio: Y
)
oppure
YX = 50
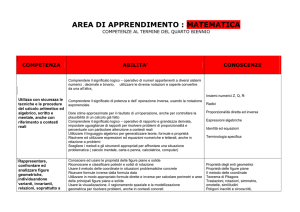
Rappresentazione grafica nel piano cartesiano:
Questa curva si chiama ramo di iperbole.
Riporto la tabella con alcune coppie X,Y della funzione
:
X
1
2
4
5
10
…
1 Funzioni: proporzionalità inversa
Y
50
25
12,5
10
5
…
XY
50
50
50
50
50
Esercizi svolti
Esercizio 1: (Ipotizziamo che 1 lavoratore impieghi 4 giorni di lavoro per realizzare un muro. Se
impieghiamo 2 lavoratori lo stesso muro sarà realizzato in 2 giorni. Ancora, se il numero
dei lavoratori sale a 4 lo stesso muro sarà realizzato in 1 giorno.
Costruisco la tabella con X (numero lavoratori) e Y (giorni impiegati):
X (nro operai)
Y (giornI)
1
2
4
XY
4
2
1
4
4
4
La funzione che descrive questa proporzionalità inversa è:
Y=
Esercizio 2: Consideriamo di voler percorrere un certo tragitto (50 km): più veloci saremo con il
nostro veicolo, meno tempo impiegheremo:
Costruisco la tabella con X (velocità) e Y (tempo impiegato):
X
Velocità
(km/h)
50
100
150
Y
Tempo (ore)
90’ = 1,5 ore
45’ = 3/4 ora
30’ = 1/2 ora
XY
(kilometri)
50 * 1,5 = 75
100 * 3/4 = 75
150 * 1/2 = 75
La funzione e il grafico che descrivono questa proporzionalità inversa sono:
Y=
2 Funzioni: proporzionalità inversa
3 Funzioni: proporzionalità inversa
Esercizi
[N.B. la difficoltà degli esercizi va da (semplice) a (impegnativo)]
Esercizio 1
Immagina di voler costruire un rettangolo con area A = 24 cm2. A tal scopo assegna valori arbitrari alla base
b e determina i corrispondenti valori che deve possedere l’altezza h.
Base b (cm)
Altezza h (cm)
1,0
…
2,0
…
3,0
…
4,0
…
6,0
…
8,0
…
12,0
…
24,0
…
Che tipo di relazione lega la base b e l’altezza h ? Costruisci il grafico cartesiano relativo ai dati della tabella
riportando sull’asse orizzontale i valori della base b e sull’asse verticale quelli dell’altezza h.
Esercizio 2
Completare la tabella e tracciare il grafico cartesiano di questa proporzione inversa:
X
20
15
12
…
6
5
2
…
Y
3
4
5
6
…
…
…
10
Esercizio 3
Scrivere almeno 3 esempi di proporzionalità inversa da voi inventati.
Esercizio 4
Per asfaltare una strada, un operaio impiega 90 giorni; trovare la formula che esprime il tempo totale
impiegato in base al numero di operai utilizzati, e rappresentare tale comportamento in un grafico
cartesiano e una tabella con alcuni valori (almeno 5 coppie).
Esercizio 5
Costruire una tabella e tracciare il grafico della funzione Y*X = 6 (utilizzando anche valori frazionari per x)
Esercizio 6
Completare la tabella e tracciare il grafico cartesiano di questa proporzione inversa:
x = Larghezza di un tessuto in metri
0,70 1,75
y = metri dello stesso tessuto necessari per ricoprire un divano
30
…
…
15
1,2
…
Esercizio 7
Per fare un regalo 4 amiche spendono 81 euro ciascuna. Quanto avrebbero speso per lo stesso regalo se
fossero state in 5 a pagare? La proporzione che risolve il problema è:
A.
4:81=x:5
B.
4:5=81:x
C.
4:5=x:81
D.
4:81=5:x
4 Funzioni: proporzionalità inversa
Esercizio 8
Trasformare in tabella il seguente grafico e trovare la funzione che lo rappresenta:
Soluzioni degli esercizi
1.
Base b (cm)
Altezza h (cm)
1,0
24,0
2,0
12,0
3,0
8,0
4,0
6,0
Funzione: Y = 24 / X
5 Funzioni: proporzionalità inversa
6,0
4,0
8,0
3,0
12,0
2,0
24,0
1,0
2.
X
Y
20
3
15
4
12
5
10
6
Funzione: Y = 60 / X
3. … esempi dello studente …
4. Y = 90 / X
6 Funzioni: proporzionalità inversa
6
10
5
12
2
30
6
10
5.
X
1
1,5
2
2,5
3
Y
6
4
3
2,4
2
6.
x = Larghezza di un tessuto in metri
y = metri dello stesso tessuto necessari per ricoprire un divano
Y = 21/X
7. Soluzione giusta: C
8. Y = 12/X
X
1
3
12
Y
12
4
1
7 Funzioni: proporzionalità inversa
0,70
30
1,75
12
1,4 1,2
15 17,5