Alcune considerazioni didattiche… - liceo scientifico Leonardo Giarre.

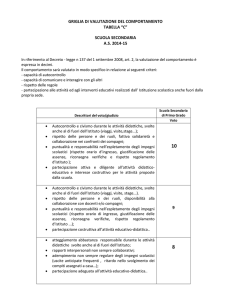
Alcune considerazioni didattiche…
Una grandezza è costante
Una grandezza è invariante
Una grandezza si conserva
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
La massa è invariante ma non si conserva
L’energia si conserva ma non è invariante
La carica si conserva ed è invariante
La velocità non si conserva e non è invariante
La velocità della luce nel vuoto è costante
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Secondo Einstein la sua teoria avrebbe dovuto chiamarsi
«Teoria degli Invarianti». Un approccio alla relatività diverso
da quello che parte dall’esperimento di Michelson e Morley
(che Einstein NON conosceva) è proprio quello basato
sull’«invarianza dell’intervallo»
𝑐 2 ∆𝑡 2 − ∆𝑥 2
È un invariante
Riferimenti: «Parabola dell’agrimensore», Wheeler-Taylor «Spacetime Physics»,
Zanichelli «La fisica dello spazio-tempo»
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Attenzione: «gli effetti relativistici sono visibili solo quando
entrano in gioco velocità prossime a quella della luce» è
vero solo in ambito meccanico!
Il campo magnetico prodotto da un filo percorso da
corrente è un effetto relativistico
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Le cariche che si muovono nel filo
producono sulle cariche che si muovono
nell’altro filo una forza proporzionale alla
velocità, la forza di Lorentz…ma per un
osservatore che si muove a una velocità
uguale a quella delle cariche la velocità è 0,
il campo magnetico NON C’È
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Ma le cariche si muovono a velocità
prossime a quella della luce?
Andiamo sul quantitativo…
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Peso specifico del rame: 8,93 kg/dm3 = 8,93 g/cm3
Con 8,93 gr di rame possiamo costruire un filo di
sezione 1 mm2 e lungo 1m…(1000mm3 = 1cm3)
Ipotizziamo che per ogni atomo di rame ci sia un
solo elettrone libero di muoversi e di fare parte
della «corrente»…quanti atomi di rame ci sono
nel filo?
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Peso atomico del rame: 63,55
In 63,55 gr di rame ci sono circa 6x1023 atomi,
quindi nel nostro filo ci sono….
N=
8,93∙6∙1023
63,55
= 8,4 ∙ 1022
atomi, e quindi elettroni che trasportano carica
elettrica lungo il filo…
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
𝐶𝑜𝑢𝑙𝑜𝑚𝑏
Ampere=
𝑆𝑒𝑐𝑜𝑛𝑑𝑜
=
𝐶𝑜𝑢𝑙𝑜𝑚𝑏
𝑚𝑒𝑡𝑟𝑜
∙
𝑚𝑒𝑡𝑟𝑜
𝑠𝑒𝑐𝑜𝑛𝑑𝑜
Quindi possiamo esprimere la corrente come
densità lineare di carica per velocità delle
cariche…
8,4 ∙ 1022 ∙ 1,6 ∙ 10−19 = 1,3 ∙ 104
È la densità lineare di carica, perché il filo è lungo
1 metro, il che significa…
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
𝐶𝑜𝑢𝑙𝑜𝑚𝑏
Ampere=
𝑆𝑒𝑐𝑜𝑛𝑑𝑜
=
𝐶𝑜𝑢𝑙𝑜𝑚𝑏
𝑚𝑒𝑡𝑟𝑜
∙
𝑚𝑒𝑡𝑟𝑜
𝑠𝑒𝑐𝑜𝑛𝑑𝑜
…che se la corrente è 1,3 Ampere (molto
grande!), la velocità media stimata degli elettroni
nel nostro modello semplificato è
10−4
𝑚𝑒𝑡𝑟𝑜
𝑠𝑒𝑐𝑜𝑛𝑑𝑜
…altro che velocità relativistiche!
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Domanda:
se
gli
effetti
dell’ordine di grandezza
relativistici
sono
𝑣2
…
2
𝑐
𝑣2
𝑐2
…e nel nostro caso
è circa 10-25, come mai ci
accorgiamo del campo magnetico prodotto dal
filo ?
…grazie al miracoloso bilanciamento delle cariche
elettriche!
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Se due persone avessero un elettrone in più ogni
miliardo, con quanta forza si respingerebbero a
100 metri di distanza?
…confrontare con la forza necessaria a spostare
la Torre Eiffel!
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Quindi, la quantità di campo elettrico e di campo
magnetico che misuriamo dipende dal sistema di
riferimento…essi sono inscindibili, per cui si parla
di campo elettromagnetico.
…Einstein partì dalle equazioni di Maxwell, il suo
articolo era «sulla elettrodinamica dei corpi in
movimento»!
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
«Le persone che vivono in un mondo curvo, ma
insistono a dire che è piatto, sono costrette a
inventare forze come la gravità…»
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Dimostrazione del principio di equivalenza della
relatività
generale
adoperando
uno
smartphone…
…o conteggio dei muoni che arrivano sulla Terra!
(e dimostrano la dilatazione del tempo della
relatività ristretta…)
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Alcune considerazioni didattiche…
Effetto fotoelettrico: perché stando dietro a un
vetro o davanti al caminetto non ci si abbronza?
Principio di indeterminazione: nell’idea che
«conoscendo tutto del presente si può prevedere
il futuro» non è la conclusione a essere sbagliata,
ma la premessa!
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione
Grazie e buon lavoro!
Direzione generale per gli ordinamenti scolastici e la valutazione del sistema nazionale di istruzione