ppt - INFN Roma1

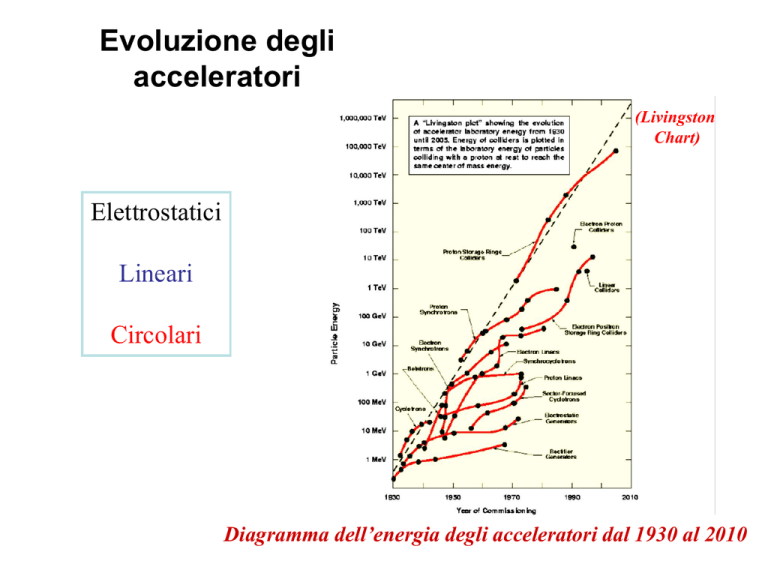
Evoluzione degli
acceleratori
(Livingston
Chart)
Elettrostatici
Lineari
Circolari
Diagramma dell’energia degli acceleratori dal 1930 al 2010
Lo sviluppo degli acceleratori è stato determinato dalla ricerca fondamentale:
Il raggiungimento di energie sempre maggiori per indagare
la struttura della materia nei componenti più ultimi
ha portato con sé l’evoluzione di tecnologie e di conoscenze
che si usano per applicazioni in moltissimi campi
L’albero del tempo delle applicazioni degli acceleratori
Un electron volt è una misura di energia: è l’energia cinetica guadagnata
da un elettrone passando in una differenza di potenziale di un Volt.
Un Volt non è una misura di energia.
Un electron volt è una misura di energia.
Un eV è un’energia molto piccola.
un eV = 1.602 x 10-19 joules
Unità di misura
dell’energia usate
negli acceleratori:
103 eV = 1 KeV
106 eV = 1 MeV
109 eV = 1 GeV
1012 eV = 1 TeV
Gli acceleratori circolari
E.O.Lawrence (1930) ebbe la
brillante idea di curvare le
particelle su una traiettoria
circolare, facendole ripassare molte
volte nello stessa cavità a
radiofrequenza.
Negli acceleratori circolari un
campo magnetico B è diretto
verticalmente; se una particella
relativistica di momento p viaggia
nel campo magnetico
perpendicolare la variazione di
momento è
dp/dt=e v x B
il raggio di curvatura della
traiettoria dipende dalla carica e
dall’energia della particella
Quali sono i componenti di un
sistema di acceleratori ?
Booster - piccolo anello che
prepara il fascio del linac per
una migliore efficienza di
iniezione
Electron Gun
Linac
Anello di accumulazione
Descrizione di un anello d’accumulazione
ELEMENTI
DAFNE: collider e+ e- all’energia della particella F
usato anche come sorgente di luce di sincrotrone
Magneti
Camera da vuoto
Cavità rf
Sistemi di diagnostica
-Posizione
-Corrente
Sistema di raffreddamento
(+ criogenico se SC)
Pompe da vuoto
Sistema di controllo
Cavi (km…)
Protezione dalle radiazioni
…
Principali magneti di un
anello
DIPOLI – determinano la traiettoria di riferimento
QUADRUPOLI – mantengono le oscillazioni di tutte le particelle
intorno alla traiettoria di riferimento
SESTUPOLI – correggono l’effetto cromatico dei quadrupoli
WIGGLERS – aumentano l’emissione di luce di sincrotrone
Equazione fondamentale
per descrivere il movimento di una particella in un acceleratore
Il moto di una particella carica è modificato dai campi
elettromagnetici

  
dp
 q E  v  B 
dt


p  m v  momento
m  mo  massa

v  velocità
q  carica

E  campo elettrico

B  campo magnetico
v
  1
c
vc
s  ct
 particella
relativistica
Campi elettrici



F  moa  qE
Accelerazione:
aumento di velocità
+ aumento di energia
con le cavità a radiofrequenza
(come nei linacs)
Accelerazione = aumento di energia
 = v/c
La variazione di
velocità è trascurabile
al di sopra di una certa
energia
Energia cinetica
Velocità delle particelle normalizzata alla velocità della
luce in funzione dell’energia
Campi magnetici
Una particella carica in un campo magnetico uniforme B
descrive un cerchio di raggio r
Dalla forza di Lorentz:
qrB  mo v
B(T ) r ( m )  3.3 E (GeV )
Rigidità magnetica
I campi magnetici sono usati negli acceleratori per guidare le particelle cariche
nelle loro traiettorie all’interno della camera da vuoto
In ogni acceleratore esiste una traiettoria di riferimento,
sulla quale viaggia la particella nominale
(energia nominale, momenti trasversali nulli).
In un acceleratore circolare tale traiettoria è un’orbita chiusa
formata da archi diy cerchio e tratti dritti
Siccome le particelle fanno traiettorie deviate
rispetto a quest’orbita
servono anche forze focheggianti che le mantengano
vicine ad essa
Frequenza di rivoluzione
vc
C
To 
v
DAFNE (Frascati)
1
fo 
To
LEP (CERN, Ginevra)
C  100 m
C  27 km
To  3.3 107 sec
To  9 105 sec
3 milioni di giri/sec
11000 giri/sec
Sistema di riferimento
y
s
x
x – orizzontale
y – verticale
s – longitudinale sulla traiettoria di riferimento
DIPOLI
Curvano la traiettoria
Campo magnetico verticale:
Bx  0
componenti nel nostro
sistema di riferimento
B y  Bo
Bs  0
B T 

m   0.3
r
E GeV 
1
1
o
QUADRUPOLI
focheggiano le traiettorie
fuori asse
campo magnetico
forze sulle particelle
Quadrupoli
y
Componenti del campo
magnetico nel nostro
sistema di riferimento:
Fy
By   g  x
Bx   g  y
Bs  0
g T / m  cte  gradiente del campo magnetico
g
k m  
" forza del quadrupolo"
Br
2
Forza di Lorentz:
la forza di focheggiamento
è lineare in x e y

 
F  q v  B 
Fx  qcgx
F y   qcgy
d2x
 kx x  0 ; kx  k
2
ds
d2y
 k y y  0 ; k y  k
2
ds
Un quadrupolo
focheggia in x
e defocheggia in y
Sequenza FODO
Una sequenza alternata di lenti focheggianti e defocheggianti ha un
effetto totale focheggiante se le distanze tra le lenti non sono troppo lunghe
Il quadrupolo che focheggia nel piano orizzontale,
defocheggia in quello verticale e viceversa
La sequenza FODO focheggia nei due piani
Esempi di magneti in un anello
dipolo
quadrupolo
Si può variare l’intensità del campo magnetico modificando
dal sistema di controllo la corrente nelle spire
Magneti permanenti
Quadrupoli usati nelle
zone di interazione di
DAFNE
per alcune applicazioni si usano i materiali a magneti permanenti:
il campo magnetico è fisso, non può essere variato con l’energia;
non consumano corrente
usati
i spesso negli ondulatori delle sorgenti di luce di sincrotrone
Wigglers e ondulatori
Negli anelli di luce di sincrotrone
per aumentare l’emissione di radiazione
si usano i Wigglers e gli Ondulatori:
serie di dipoli a campi alternati
in cui le particelle compiono un’oscillazione
ed emettono luce la cui lunghezza d’onda
dipende dal campo del wiggler
Oscillazioni di betatrone
Una particella con l’energia nominale e con x  x'  y  y' 
segue la traiettoria nominale
e passa al centro dei quadrupoli dove il campo magnetico è nullo
Q
Q
x
Traiettoria nominale
Se la sua posizione cambia per qualche motivo,
passa fuori asse nei quadrupoli
e oscilla intorno alla traiettoria nominale:
Oscillazione di betatrone
0
Q
Equazioni di Hill:
Oscillatore pseudoarmonico
Termine forzante periodico
D

x' '  2
s
 x ' ' k x ( s ) x  0

 y ' ' k y ( s ) y  0
k x (s) 
g (s)
Br
k y (s)  
g (s)
k x ( s )  k x ( s  L)  funzione periodica
L  lunghezza circonfere nza

Br
1
r (s)
2
Soluzione
Posizione
Angolo
(divergenza)
y( s )  A  ( s ) cosf ( s )  d 
A
sinf ( s )  d    ( s ) cosf ( s )  d 
y' ( s )  
 ( s)
y : coordinata trasversa (x o y)
Funzioni di Twiss
A, d : costanti di integrazione
 : ampiezza di betatrone
f : avanzamento di fase di betatrone
ds
f ( s)  
 ( s)
 ( s)
1  ( s )
 ( s)  
2 s
1   2 ( s)
 ( s) 
 ( s)
Piano orizzontale : particelle con energia
diversa da quella nominale
Una particella con l’energia diversa da
quella nominale, al passaggio in un dipolo
segue una traiettoria diversa da quella
nominale
L’equazione del moto
è non omogenea
nel piano orizzontale:
1 E
x' ' k x ( s ) x 
r Eo
La soluzione è la somma della soluzione all’equazione omogenea, x(s)
e di un termine proporzionale alla deviazione di energia
E
x ( s )  x  ( s )  D( s )
Eo
D(s) è la funzione di dispersione, periodica,
viene determinata dai dipoli e dai quadrupoli
Se xo(s) è l’orbita chiusa di
riferimento, per ogni energia Ek
esiste un’orbita chiusa,
E k  Eo
x k ( s )  x o ( s )  D( s )
Eo
intorno alla quale oscillano di
betatrone le particelle con energia Ek
Negli anelli in cui i dipoli curvano soltanto sul piano orizzontale
esiste solo la funzione Dx(s), dispersione orizzontale
Spazio delle fasi di una particella
Area dell’ellisse =
invariante del moto
a energia costante
 y 2  2 y y'  y'2  const  area dell ' ellisse
, , , variano lungo s; l’area dell’ellisse è invece costante
EMITTANZA
 y 2  2 y y'  y'2  const    area dell ' ellisse
L’area dell’ellisse che contiene tutte le particelle del fascio è
l’emittanza
Momento trasverso
I parametri di Twiss
definiscono la forma e
l’inclinazione
dell’ellisse nello spazio
delle fasi,
l’emittanza la sua
area.
Dimensione trasversa
L’emittanza si conserva qualunque sia la forza magnetica
che agisce sulla particella:
Teorema di Liouville
Le unità di misura dell’emittanza sono
m rad
(dimensione * divergenza)
“Nelle vicinanze di una particella, la
densità delle particelle nello spazio delle
fasi è costante se le particelle si muovono
in un campo magnetico esterno o in
qualunque campo in cui le forze siano
conservative”
Spazio delle fasi in diversi punti dell’acceleratore
Caratterizzazione del fascio
Le particelle di un fascio in un acceleratore non hanno tutte la stessa energia e posizione
L’energia, la posizione e il momento trasverso hanno distribuzioni gaussiane
Il pacchetto di particelle è un
ellissoide a 6 dimensioni:
y
Posizione - momento orizzontale
Posizione - momento verticale
Energia - posizione longitudinale
s
distribuzione
x
coordinata
Caratterizzazione di una particella
E/E
x’
y’
x
y
Ogni particella ha il suo invariante nei 3
“spazi delle fasi”:
orizzontale, verticale e longitudinale
l
Dimensione del fascio
Quanto misura il pacchetto di elettroni o positroni all’interno della camera da vuoto?
La dimensione trasversa
del fascio è
(rms della gaussiana)
 ( s )   ( s )
emittanza
Negli anelli di collisione e+ enel piano orizzontale la
 è tipicamente dell’ordine dei mm
mentre nel piano verticale
è circa 100 volte minore
Abbiamo visto:
Orbita chiusa
Oscillazioni di betatrone intorno ad essa
Diverse orbite chiuse per diverse energie
Equazioni del moto
Parametri di Twiss e dispersione periodici
…
Trattamento matematico: MATRICI
Ogni particella è caratterizzata da 6 coordinate
Due orizzontali:
x, x’
Due verticali:
y, y’
Due longitudinali:
s, E/E
VETTORE
 x 


 x' 
 y 
 y' 


 s 
 E / E 


Il modo in cui il vettore di una particella si trasforma
quando passa per un elemento dell’anello
viene descritto dalla matrice dell’elemento
Tratto dritto:
1

0
0

0
0

0
l
1
0
0
0
0
0
0
1
0
0
0
0
0
l
1
0
0
0
0
0
0
1
0
0

0
0

0
0

1 
Quadrupolo
Dipolo
 cos 
 1
  sin 
 r

0

0


0

0

r sin 
0
0
cos 
0
0
0
0
0
0
1 r
0 1
0 0
0 0
Conoscendo le caratteristiche di un elemento
La sua matrice di trasporto è definita

 cos k l

  k sin k l

0


0

0


0

0 r (1  cos  ) 


0
sin 


0
0

0
0


1
0

0
1

1
sin k l
k
cos k l
0
0
0
0
0
0
cosh  k l
 k sinh  k l
0
0
,…

0 0

0
0 0
1
sinh  k l 0 0 

k
cosh  k l
0 0

0
1 0
0
0 1 
0
L’anello è descritto matematicamente da una serie di matrici.
Sia per la progettazione che per la simulazione della dinamica del fascio
vengono usati codici di calcolo
Esempio di simulazione
di una regione di anello:
funzioni  di Twiss (nera e rossa)
e Dispersione (verde)
Frequenze di betatrone
Qx , y
1

f x , y ( s )ds

2
Il numero di oscillazioni di betatrone in un giro
è chiamato
‘numero di betatrone’ o ‘tuno’
(dall’inglese ‘tune’)
Siccome le oscillazioni vengono guidate dai quadrupoli,
il tuno dell’anello viene determinato dai campi quadrupolari:
più forti sono i quadrupoli, più rapide sono le oscillazioni,
maggiori sono i tuni
Risonanze
La frequenza di betatrone non è un numero intero: se così fosse, qualunque
perturbazione ci fosse in un punto dell’anello sarebbe vista sempre
con la stessa fase, e il suo effetto cumulativo potrebbe essere
distruttivo per la particella
ci sono quindi zone ‘proibite’
nel diagramma dei tuni:
le risonanze
nQ x  mQ y  p , n, m , p interi
Errori di posizionamento o campo
… quanto detto finora si riferisce a un acceleratore ‘ideale’
Nella realtà è impossibile costruire una macchina perfetta:
gli errori di posizionamento dei magneti o di intensità del campo
magnetico costituiscono un elemento della macchina.
Il loro trattamento matematico fa parte della fisica degli acceleratori
tanto quanto ne fa parte l’elettromagnetismo
Orbita chiusa ideale
Caso più semplice:
errore di posizionamento di un quadrupolo
crea un’orbita chiusa che si discosta da quella ideale
lungo tutta la macchina
Orbita chiusa dovuta a un errore
y
posizione della traiettoria: dx
Fy
Il quadrupolo agisce come un dipolo
By = g x
e dà alla traiettoria un angolo
d proporzionale a gx
L’orbita chiusa che ne deriva è data da
xk ( s ) 
d ( Bl )k
1
2 sin Q x Br
 ( s ) k cos f ( s )
Se Qx fosse intero l’orbita sarebbe infinita -> instabile
Cromatismo
L’effetto focheggiante o defocheggiante di un quadrupolo
dipende dall’energia della particella
E = Eo
E > Eo
Il tuno della particella con energia nominale
è diverso dal tuno di una particella con energia diversa
C x, y 
E
Q x , y
E Eo
= cromatismo
Sestupoli
Il cromatismo non corretto crea
instabilità al di sopra di certe correnti
(effetto testa-coda: scoperto ad ADONE,
Frascati)
Per correggerlo si usano i sestupoli
B x  2 Sxy
By  S( x2  y2 )
Il sestupolo si comporta come un quadrupolo
con un gradiente proporzionale allo spostamento trasversale
I sestupoli introducono i campi non lineari nell’acceleratore
Apertura dinamica:
zona stabile all’interno dell’anello
La presenza di campi non lineari implica
che il moto della particella
non è più un’ellisse nello spazio delle fasi
(non basta l’equazione di Hill).
Il moto diventa più disordinato e può portare a
Instabilità.
L’attraversamento delle risonanze
può portare a perdita della particella
Solo campi lineari
Dipoli e quadrupoli
Sestupoli
Ottupoli
…..
simulazione dello spazio delle fasi con forti campi non lineari
Piano
longitudinale
Il fascio di particelle viene iniettato
nell’anello con l’energia
acquistata nel LINAC.
Durante il passaggio attraverso i
dipoli perde energia emettendo
“luce di sincrotrone”.
Quando passa nella cavità rf ,
ri-guadagna energia.
Cavità rf

E  q  Edt  qV
gap
t
V  Vˆ sin   rf dt '  Vˆ sin f ( t )
0
La frequenza rf del campo elettrico della
cavità, frf , è un multiplo intero della
frequenza di rivoluzione, fo
f rf  2  rf  h f o
h  numero armonico
La particella sincrona è la particella
nominale, che arriva alla cavità dopo un
giro, all’istante in cui la fase è quella giusta
per il guadagno nominale di energia
Durante l’accelerazione tutti i campi magnetici vengono
aumentati per seguire l’aumento di energia
Quando l’energia del fascio arriva al valore nominale dell’anello,
la cavità rf restituisce alle particelle solo l’energia che esse perdono
per luce di sincrotrone durante il giro.
Le altre particelle del fascio, oscillano intorno alla particella sincrona,
con lo stesso principio della stabilità
Analogamente ai piani trasversali,
si possono scrivere le equazioni delle
oscillazioni longitudinali,
dove le coordinate della particella sono
Oscillazioni di sincrotrone
Zone stabili
di fase nei linacs.
f  f  f s
fase
E  E  E s energia
2

s
sin f  sin f s   0
f 
cos f s
Radiazione di sincrotrone
Una particella carica che viaggia in una traiettoria curva emette fotoni,
la cui energia dipende dalla massa e dall’energia della particella e dal
raggio di curvatura della traiettoria
Una particella carica che viaggia in una traiettoria curva perde energia.
In un anello di accumulazione l’energia persa viene compensata dalle
cavità a radiofrequenza
cavità a rf
4 ro E 4
U
2 3
3 mc  r
Energia emessa per giro
Le particelle più leggere emettono più energia.
Come sorgenti di radiazione vengono usati
acceleratori di elettroni o positroni
Emissione di luce di
sincrotrone
Campo magnetico
4 ro E
E B
U

3
2 3
3 mc 2  r
mc 
4
E
m
(GeV) (MeV)
DAFNE
1
0.51
0.009
ELETTRA
5.6
2
0.1
ESRF
23
6
1
LEP
3000
100
1500
3
Massa
E/giro
r
Energia della particella
Raggio di curvatura della traiettoria
Anello di luce di sincrotrone:
nella camera da vuoto dove le particelle curvano si inseriscono finestre di diamante
da dove la luce viene estratta e trasportata alle linee degli esperimenti
Quali sono i ‘limiti’ delle sorgenti di
radiazione ?
Energia
Intensità
Aumentando l’energia di un acceleratore circolare
si aumenta la perdita di energia per luce di sincrotrone:
cavità rf
dipoli
dimensioni totali dell’anello
tutti i campi magnetici
devono essere dimensionati adeguatamente
Intensità: effetti collettivi
Abbiamo visto come
il moto di una singola particella in un
acceleratore è determinato dai campi
magnetici creati dai dipoli e quadrupoli, dal
sistema rf, dalle condizioni iniziali
e dalla radiazione di sincrotrone
Tutte le particelle contenute in un
fascio ad alta intensità sono una
corrente elettrica con una carica
non trascurabile
Esempio:
N=5 10 10 per bunch
n = 100
Qtot= 1.6 10 –19 C x 100 x 5 10 10 = 8 10-7 C
I = Q/t = Q fo = 3 10 –6 1.6 10-7 = 2.4 A
I fasci di particelle agiscono
come sorgente di campi
elettromagnetici:
self fields
Questi campi interagiscono
con ciò che li circonda,
vengono modificati dalle
condizioni al contorno
(camera da vuoto, cavità,
ecc) e agiscono a loro volta
sul fascio stesso
Ciò può dare origine a una variazione delle frequenze proprie del fascio
(frequenze di betatrone e sincrotrone),
può portare a:
instabilità,
o modifica della distribuzione del fascio,
o allungamento dei pacchetti.
Questi fenomeni si chiamano effetti collettivi
e sono naturalmente collegati al numero di particelle presenti nel fascio
I sistemi che ‘controllano’ gli effetti collettivi sono diversi:
Impedenza di ogni elemento ‘visto’ dal fascio
(camera da vuoto, soffietti, cavità, elementi di diagnostica,….)
Vuoto dinamico
Sistema di feedbacks
…
Camera da vuoto
esempio di elementi
arco di DAFNE
soffietto
Diagnostica
Esempio di monitor di posizione:
il segnale elettrico del fascio viene raccolto
da 4 elettrodi, La tensione indotta permette
di risalire alla posizione in x e y del centroide del fascio
Sistema di
controllo
Le informazioni sullo stato di ogni elemento dell’acceleratore
+ le informazioni sulla posizione, intensità, stato del fascio
lette dagli elementi di diagnostica
vengono trasportate alla sala di controllo
dove l’operatore controlla la situazione e
agisce sugli elementi dell’accelaratore
per mantenere e ottimizzare le performance dell’insieme.
Eventuali malfunzionamenti dei vari sottosistemi vengono segnalati
in tempo reale
Collisori particella-antiparticella
Particella-antiparticella circolano in versi opposti
nello stesso anello (es. ADONE)
Vantaggio rispetto ad un fascio contro una targhetta fissa: stessa
E nel centro di massa ma con molta meno E del fascio:
Collisore
W  2 E1 E2
Targhetta fissa di e-
W  2E mt  2mt
Per avere 1 GeV nel centro di massa: W = 1 GeV
E1 = E2 =.5 GeV
E = 1000 GeV
Vantaggio e+e- rispetto a p anti-p: e+e- puntiformi
2
Luminosità
• Numero di particelle prodotte nell’interazione:
Luminosità
Sezione d’urto
N N 
L 
A
Numero di particelle collidenti
Sezione trasversa dei fasci all’interazione
• Limite principale sulla L: interazione fascio-fascio
particella di un fascio vede l’altro fascio come una lente
convergente  oscillazioni di betatrone incontrollabili
entro un certo limite
Vantaggio dei 2 anelli separati (DAFNE)
Se volete saperne di più….
CAS: CERN Accelerator School
Proceedings : http://cas.web.cern.ch/cas/CAS_Proceedings.html
M. Sands, “The Physics of Electron Storage Rings”, SLAC Report 121 (1970)