Modelli atomici e molecolari

CORSO di PERFEZIONAMENTO
in FISICA MODERNA
modelli atomici e molecolari
7 settembre 2004
premessa: modelli e realtà
 conti e conticini a scuola
 l’atomo verità
 il Lego quantistico e le molecole
 spettri di ogni genere
 chi ce lo fa fare?

1
L’atomo ed i suoi modelli
proprietà fondamentali degli atomi:
cosa stiamo cercando?
 spettri atomici
 modelli, modelli …
 l’atomo di idrogeno nella fisica
quantistica
 oltre l’idrogeno

2
Proprietà fondamentali degli
atomi
lunghezza d'onda  (m)
la materia è composta da atomi di dimensioni molto
nm 400 nm di 10-10 m);
piccole (diametro medio700dell'ordine
10
10
10
10
10
10
10
10
10
10
10
10
10
 gli atomi sono stabili (forze di coesione interna in
equilibrio);
Raggi
Gamma
IR cariche
Raggi X

gliLunghe
atomi sono
da
elettriche
di segno
Onde composti
Radio
Onde
V UV
opposto in numero eguale (elettricamente neutri);
LW AM FM TV SW
 gli atomi emettono ed assorbono radiazione
10
10
10
10
10
10
10
10
10
10
10
10
10
elettromagnetica
in uno
spettro
estremamente
ampio,
microonde, infrarossi, visibile,
raggi X.
frequenza ultravioletto,
 (Hz)

8
6
3
2
4
5
-2
0
7
9
-4
11
-8
-6
13
15
17
-10
19
-12
21
-14
23
-16
25
3
Modelli di Thompson e Rutherford
4
Modello di Bohr
=LIM/(1-n02/n2)
5
Modello di Bohr
Il conticino!
T=mv2/2; U=Ze2/(40r)
F=mv2/r=Ze2/(40r)  T=Ze2/(80r)
E=T+U= Ze2/(80r)
T=L2/(2mr2)=n2ħ2/(2mr2)=Ze2/(80r)
r=rn= 40n2ħ2/(Zme2)=a0n2/Z,
L=mvr= nħ
dove
a0=40ħ2/(me2)=0.0529 nm
E=En=Z2E0/n2,
dove
E0=me4/(32202ħ2)=2.181018 J=13.6 eV.
6
Modello di Bohr
L'elettrone cede ed assorbe energia nelle transizioni fra
diversi stati stazionari tramite l'emissione e
assorbimento di quanti di radiazione elettromagnetica,
fotoni di energia regolata dalla relazione di Bohr:
En1n2=h12=En1En2=Z2E0(1/n22-1/n12)
2
2
n

n
12  Z 2 R c 1 2 2 2  Z 2 (3.29  1015 Hz )(1 / n22  1 / n12 )
n1 n2
R=E0/hc=me4/(64302ħ3c) = 1.0974105 cm1
7
Modello di Bohr
n=
emissione/
n=4
assorbimento
assorbimento
n=3
13.6 eV
n=2
Balmer
(V)
instabile
12.8 eV
12.1 eV
10.2 eV
Lyman
n=1
(UV)
stabile
COSA GLI MANCA? Non funziona per atomi con 2 o più
elettroni; non riesce a predirre le intensità delle linee; non è
“indeterminato”!
8
L’atomo di idrogeno in fisica quantistica
Lo STATO FISICO del sistema:
(r,,)
L’operatore Hamiltoniano H=T+U
U(r)=e2/(40r2)
2  2
2
2 
2
 2  2  2   
T 

2m  x
2m
y
z 
L’equazione di Schroedinger
H=E
  2  2 
1  
 
1
2 




  U ( r )  E 
 sin 

2m  r 2 r r r sin   
  r 2 sin 2  2 
2
9
L’atomo di idrogeno in fisica quantistica
QUANTIZZAZIONE SPAZIALE e MOMENTO ANGOLARE
L=[l(l+1)]1/2ħ,
Lz=mlħ, ml=0,1,2,….l
ml
Lz
cos  

L
l (l  1)
10
L’atomo di idrogeno in fisica quantistica
 n ,l ,ml (r , , )  Rn ,l (r )l ,ml () ml ()
1
me4
E  E ( n)   2
n 32202
2
quantizzazione dell’energia
 nlml (r , , )   1
r exp   Zr / na0 
l
m m 2
2
n l 1

j 0
Z l 1
nl  2 a0l 1
Z  n  l  1 ! n  l ! l  m ! 2l  1
a0  l  m  !

l m


2 

(1) j  2l  2 j !
 2Zr / na0 
m
l  m 2 j
cos
 

  sin   
n

l

j
!
j
!
n

l

j

1
!
j
!
l

j
!
l

m

2
j
!








j

0




n l  j 1
 2 sin  m  (m  0)

 1
(m  0)

 2 sin  m  (m  0)
11
L’atomo di idrogeno in fisica quantistica
2
P(V )    (r , , ) dV   Rnl (r )lml () ml () r 2 sin drd d  
2
V
V
2
2
  Rnl (r ) r dr   lml () sin d    ml () d 
2
2

r

1.4
R20 (r ) 
R21 (r ) 
2
a0 
3/ 2
e  r / a0 ,
1.2
1
1
2 2 a 0 
3/ 2
1
2 6 a 0 
3/ 2

r
 2 
a0

re
 r / a0
  r / a0
e
,

n,l=1,0
0.8
P(r)
R10 (r ) 
0.6
n,l=2,1
n,l=2,0
0.4
.
0.2
0
0
1
2
3
4
r
5
6
7
12
L’atomo di idrogeno in fisica quantistica
densità radiali ns (l=0)
13
L’atomo di idrogeno in fisica quantistica
densità radiali np (l=1)
14
L’atomo di idrogeno in fisica quantistica
15
L’atomo di idrogeno in fisica quantistica
densità radiale a simmetria sferica (s, l=0)
16
L’atomo di idrogeno in fisica quantistica
densità radiale a simmetria cilindrica (p, l=1)
17
L’atomo di idrogeno in fisica quantistica
ORBITALI !!!
1s
2s
3s
4s
18
L’atomo di idrogeno in fisica quantistica
ORBITALI !!!
2p
3p
4p
19
L’atomo di idrogeno in fisica quantistica
ORBITALI !!!
3d
4d
4f
20
L’atomo di idrogeno in fisica quantistica
ORBITALI !!!
dalla famiglia l=0
21
L’atomo di idrogeno in fisica quantistica
ORBITALI !!!
dalle famiglie l > 0
n,l,m=25,24,24
n,l,m=25,24,0
n,l,m=25,24,12
22
Atomi a più elettroni



inadeguatezza dell’equazione di Schroedinger
metodi variazionali e perturbativi
il caso più “semplice”: l’atomo di elio
Z=1
Z=2
E=E(Z=1)+E(Z=2)+E12 ?
REGOLARITA’
Fluoro (Z=9) della
SEQUENZA delle PROPRIETA’
e Neon (Z=10)
CHIMICO
– FISICHE?
23
L’atomo di elio e le simmetrie quantistiche
U 
2
2
r12
2
Ze
Ze
e


40 r1 40 r2 40 r12
r1
approx. di ordine “zero”: elettroni indipendenti,
“idrogenoidi”, schermati
r2
funzione d’onda dell’atomo
atomo   a (1)b (2)
minimizzazione dell’energia, ma la funzione d’onda è sbagliata:
per indistinguibilità quantistica vale anche la
atomo   a (2)b (1)
Con la stessa energia: è la degenerazione di scambio (fra stati elettronici diversi, a e b)
24
L’atomo di elio e le simmetrie quantistiche
U 
2
2
r12
2
Ze
Ze
e


40 r1 40 r2 40 r12
r1
r2
La densità di probabilità orbitale deve essere
simmetrica per lo scambio dei due elettroni 
atomo (A,S)   a (1)b (2)   a (2)b (1)
1
2
1o2
2
1
2o1
A seconda del segno (±) cambia la simmetria di  e l’energia: (A) è piccola
quando gli elettroni sono “spesso vicini”. (S) è più grande. L’atomo di elio vive in
due diversi stati (sia per energia che per funzione orbitale).
25
L’atomo di elio e le simmetrie quantistiche
r12
E’ NECESSARIO INCLUDERE I NUMERI QUANTICI DI
SPIN (momento angolare intrinseco, s=1/2, S=0 oppure S=1).
Lo stato S=0 è antisimmetrico, S=1 è simmetrico per scambio
di elettroni.
r1
r2
La funzione d’onda totale è data dal prodotto delle parti
orbitale e di spin, Sperimentalmente si osserva che essa
è sempre antisimmetrica per scambio degli
elettroni
tot = orb(S)  spin(A) oppure tot = orb(A)  spin(S)
Conseguenza:
26
Principio di Esclusione di Pauli
In un singolo sistema non possono esistere due o più elettroni
nello stesso stato quantistico
He (Z=2): n1=n2=1; l1=l2=0; m1=m2=0;
ms1=+1/2, ms2=1/2
stato fondamentale elettronico 1s2 (↑↓)
equivalente alla richiesta di antisimmetria totale della funzione d’onda (che è più generale,
non dipende dalla condizione di indipendenza delle particelle). Si applica ai FERMIONI.
 a (1)

1  b (1)
 abc... (1, 2,3,...) 
N !  c (1)


a (2) a (3)
b (2) b (3)






27
“Aufbau” atomico




Z=3, 1s2 2s1
Z=4, 1s2 2s2
Z=5 ... 10, 1s2 2s2 2p1 ... 2p6
Z=11, 1s2 2s2 2p6 3s1
...
6p
5d
4f
6s
5p
4d
5s
4p
3d
4s
3p
3s
2p
2s
1s
Sequenza energetica per gli elettroni
ESTERNI o di VALENZA
gusci K L M N O P
n
12 3 4 5 6
28
Tabella periodica degli elementi
1s1
2s1, 2s2
3d1 ... 3d10
1s2
2p1 ... 2p6
29
Tabella periodica degli elementi
30
Proprietà degli elementi
31
altri spettri ...
Amplificazione di luce tramite emissione
emissione
X da giusci...interni
stimolata
di radiazione
L
A
S
E
R
intensità

serie K
0.01
serie L
M

serie M
0.1
1.0
emissione
spontanea
lunghezza d’onda (nm)
L
assorbimento
indotto    
emissione
indotta
K
32
MOLECOLE

per iniziare:
ione - molecola idrogeno
la soluzione quantistica:
sovrapposizione!
GP
G
PUU
R
+
+
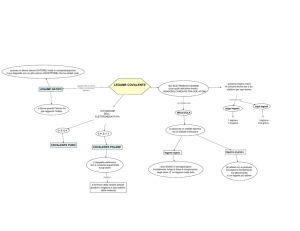
LEGANTE
B
A B
A
ANTILEGANTE
33
MOLECOLE

r2
r1
conti, conti …
+
R
+
Z Ae 2
Z B e2 Z A Z B e2
H 
e 
A 
B 


2me
2M A
2M B
40 r1 40 r2 40 R
2
2
2
E
approccio variazionale
nell’approx. a nuclei fermi
funzione di “prova” LCAO-MO
energia minima
E


* H dV




*dV
  c11sA  c21sB
H AA  H BB
, H AA( BB )   1s A ( B ) H 1sA ( B ) dV , S   1sA 1sB dV
1 S
funzioni d’onda “leganti” / “antileganti”, =1sA±1sB
34
Le curve dell’energia molecolare
35
Orbitali molecolari ,  LCAO
36
Orbitali molecolari ,  LCAO
37
Orbitali Ibridi: verso la chimica organica
configurazione di riferimento dell’atomo di carbonio, Z=6, 1s22s22p2
38
Metodi di (super)calcolo per la struttura
e dinamica molecolare
meccanica molecolare (angoli e molle)
LCAO – MO (centri atomici)
Hartree-Fock (funzioni “esatte”)
funzionale densità (funzione della
densità elettronica)
39
Rotazioni e vibrazioni molecolari
Studio dei moti nucleari: molto più lenti di quelli elettronici
Spettroscopia microonde ed infrarossa, rotazioni e vibrazioni.
<stato iniziale> ± radiazione  <stato finale>
Tecniche IR e Raman
campione
IR: eccitazione continua, studio
dell’assorbimento/trasmissione,
individuazione di righe
Sorgente
IR
RAMAN: eccitazione
monocromatica, osservazione
della luce diffusa (Rayleigh e
Stokes)
Laser
visibile
Rivelatore
IR
riferimento
campione
Rivelatore
visibile
40
Rotazioni e vibrazioni molecolari
dipoli elettrici, polarizzabilità, onde elettromagnetiche, transizioni
Le molecole scambiano (in modo risonante) energia con il campo e/m
tramite il loro dipolo elettrico (permanente o indotto). Se c’è variazione di
dipolo elettrico, la molecola è “attiva” secondo lo schema IR, se c’è
variazione della polarizzabilità è attiva secondo lo schema Raman.
Gli spettri rotazionali-vibrazionali si spiegano in termini di transizioni fra
stati causate dagli “elementi di matrice” (quantistica) associati agli
operatori di dipolo o quadrupolo elettrico.
IRab
Ramanab
a ˆ b

2
a ˆ b
2
a
( x)( x)b dx

a
2
( x)( x)b dx
2
41
Rotazioni molecolari
Ecl=I2/2=L2/2I, I=re2
L2=ħ2J(J+1),
EJ=ħ2J(J+1)/2IBJ(J+1)
(approx. rotore rigido, regola selezione J=J±1)
EJ= BJ(J+1)DJ2(J+1)2 (correzione “centrifuga”)
L=4
L=3
L=2
L=1
L=0
42
Vibrazioni molecolari
L’approssimazione di Born-Oppenheimer per iniziare, M~2000m
L’oscillatore armonico in meccanica quantistica
Ev=(v+1/2)ħ
Livelli equispaziati di energia vibrazionale: si osservi
(1) l’energia di punto zero
(2) La possibilità di calcolare  e dunque la costante di forza del legame
atomico nella molecola
Situazione realistica: anarmonicità dell’interazione,
potenziali di Morse, Poeschl-Teller, etc.
Vmorse (r )  V0{exp[2(r  re )]  2exp[(r  re )]}
E (v)  (v  1/ 2)  x(v  1/ 2) 2
43
Vibrazioni molecolari
Molecole poliatomiche, modi normali
approccio classico masse e molle: che esercizio!
disaccoppiamento delle interazioni
1
1  dq j 
2
U    jq j , T  

2 j
2 j  dt 
2
Moti atomici in fase, con eguali
ampiezze e frequenze
44
Vibrazioni molecolari (a cosa serve)
SPETTROSCOPIA DI OGGETTI “COMPLICATI”
IL RUOLO DELLE SIMMETRIE E DELLE TECNICHE GRUPPALI
ANALISI FUNZIONALE
CHIMICA FOTOSELETTIVA
ECCITAZIONI ROVIBRAZIONALI ED ELETTRONICHE (F-C)
45
Vibrazioni molecolari (a cosa serve)
SPETTROSCOPIA DI OGGETTI “COMPLICATI”
IL RUOLO DELLE SIMMETRIE E DELLE TECNICHE GRUPPALI
ANALISI FUNZIONALE
CHIMICA FOTOSELETTIVA
ECCITAZIONI ROVIBRAZIONALI ED ELETTRONICHE (F-C)
46