La geometria delle
trasformazioni
Il programma di Erlangen
Geometria e trasformazioni
Programma di Erlangen
(Felix Klein, 1872)
La geometria è lo studio delle proprietà invarianti
rispetto ad un gruppo di trasformazioni.
Le proprietà geometriche delle figure non sono
determinate dalla forma della figura ma dalle
trasformazioni che possono agire su di essa.
Geometria del piano
: piano della geometria elementare
figura piana: un qualsiasi sottoinsieme del piano
(punti, rette, triangoli, rettangoli, circonferenze,
dischi, etc.)
trasformazione piana: una qualunque funzione
biunivoca T : .
Composizione di trasformazioni
Date due trasformazioni piane
T1 : e T 2 :
la trasformazione composta è la funzione
T2 T1 :
definita applicando prima T1 e poi T2, ossia ponendo
(T2 T1)(P) = T2(T1(P))
per ogni punto P del piano .
La composizione di due funzioni biunivoche è
ancora una funzione biunivoca
Quindi, la composizione di due trasformazioni
piane è ancora una trasformazione piana.
L’insieme S() di tutte le trasformazioni del piano
è chiuso rispetto alla composizione (e possiede
una struttura di gruppo).
Struttura di gruppo di S()
la composizione è un’operazione interna;
la composizione è un’operazione associativa:
T1 (T2 T3) = (T1 T2) T3
• esiste un elemento neutro, la funzione identità E :
P P, tale che
TE=ET=T
• esistono le trasformazioni inverse: per ogni
trasformazione T esiste una trasformazione
inversa T-1 tale che
T T-1 = T-1 T = E.
Figure piane equivalenti
Due figure piane F1 ed F2 sono equivalenti, o
congruenti, se esiste una trasformazione piana T
che porta la prima figura nella seconda, ossia se
F2 = T(F1).
In questo modo abbiamo definito una relazione
tra le figure del piano che generalizza la relazione
di uguaglianza. Più precisamente questa relazione
è una relazione di equivalenza.
Relazioni di equivalenza
riflessività: ogni figura è equivalente a sé stessa;
simmetria: se una figura F1 è equivalente ad una
figura F2 allora anche la figura F2 è equivalente
alla figura F1;
transitività: se una figura F1 è equivalente ad una
figura F2 e la figura F2 è a sua volta equivalente ad
una figura F3 allora la figura F1 è anch’essa
equivalente alla figura F3.
Geometrie piane
Dare una geometria piana significa assegnare un
sottogruppo G di S() delle trasformazioni
ammissibili.
La geometria è lo studio delle proprietà che
restano immutate comunque si applichi una
delle trasformazioni ammissibili. Ossia una
proprietà geometrica di una figura piana F è una
proprietà che vale per F e per ogni altra figura T(F)
che si può ottenere da F mediante una
trasformazione piana T appartenente al gruppo G.
Classificazione
Due figure piane F1 ed F2 sono equivalenti, o
congruenti, se esiste una trasformazione piana T
appartenente al gruppo G che porta la prima
figura nella seconda: F2 = T(F1).
Affinché questa relazione sia una relazione di
equivalenza occorre che G sia un gruppo.
Classificare le figure significa determinare le classi
di equivalenza, ossia i tipi di figure.
Geometria euclidea metrica
Supponiamo che sia dotato di un’unità di misura
e quindi di una distanza d(P,Q) tra i punti.
Una isometria è una trasformazione T :
che conserva le distanze, ossia tale che
d(T(P),T(Q)) = d(P,Q)
per ogni punto P e Q del piano.
Esempi: traslazioni, rotazioni, simmetrie.
Figure invarianti: rette, rette parallele, rette
perpendicolari, triangoli, circonferenze.
Proprietà invarianti: lunghezze, aree, angoli.
Geometria euclidea simile
Una similitudine è una trasformazione
T : che conserva i rapporti tra le
distanze.
Esempi: traslazioni, rotazioni, omotetie.
Proprietà invarianti: rapporti tra le
distanze, parallelismo tra rette, ampiezza
degli angoli, rettangoli, il teorema di
Pitagora.
Proprietà non invarianti: lunghezze, aree.
Le isometrie sono particolari similitudini.
Allora ogni proprietà simile è anche una
proprietà metrica.
Geometria affine
Una affinità è una trasformazione T : che
conserva le rette, ossia l’allineamento dei punti.
Proprietà invarianti: parallelismo di rette,
congruenza tra segmenti, ellissi, le mediane di un
triangolo si intersecano in un unico punto .
Proprietà non invarianti: lunghezze, angoli,
rapporti tra distanze, circonferenze, rettangoli.
Le isometrie e le similitudini sono affinità.
Le Trasformazioni Geometriche
Vogliamo conoscere le relazioni che
sussistono tra gli oggetti geometrici
quando subiscono trasformazioni
La trasformazione identica o identità è quella che
associa ad ogni punto se stesso
Si dice involutoria una trasformazione che, applicata
due volte, coincide con la trasformazione identica
Si chiamano invarianti le caratteristiche che
rimangono inalterate
Varianti le caratteristiche che si modificano
Elementi uniti gli elementi che hanno per trasformati
se stessi
Invarianti
Le principali caratteristiche che una
trasformazione può lasciare invariate sono:
La Lunghezza dei segmenti
L’ampiezza degli angoli
Il parallelismo
Le direzioni
Il rapporto tra i segmenti
L’orientamento dei punti del
piano
Trasformazioni geometriche
Si possono suddividere in tre categorie:
Trasformazioni che si ottengono mediante
deformazioni (esempio: disegno su tela
elastica)
Trasformazioni che si ottengono per
proiezioni (esempio: ombra di un oggetto)
Trasformazioni che si ottengono mediante
movimenti (esempio: immagine riflessa)
La figura rappresenta un’incisione di
M.C.Escher (1898-1972).
Essa fornisce un esempio di
riflessione sulla sfera; è interessante
notare che le linee rette degli spigoli
della stanza dove si trova l’artista
sono diventate linee curve.
Classificazione delle
trasformazioni basata
sugli invarianti
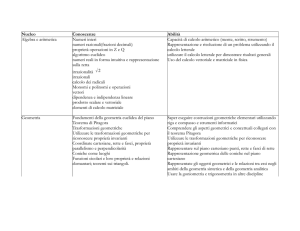
Le classificazioni rappresentate nello schema sono via via più restrittive. Vengono
identificate in base a numero e tipo di proprietà mantenute dalle figure dopo una
trasformazione.
TOPOLOGIA
Esistono altre trasformazioni che non portano rette in rette: deformazioni continue
che conservano le “intersezioni”.
I ponti di Königsberg
OMEOMORFISMI
Gli omeomorfismi, detti anche trasformazioni topologiche,
conservano la continuità
A curve chiuse corrispondono curve
chiuse
A curve aperte corrispondono curve
aperte
A curve intrecciate corrispondono
curve intrecciate con lo stesso numero
di nodi( i punti in cui le curve
intersecano se stesse )
Se un punto è intersezione di due
curve, il punto che gli corrisponde
risulta intersezione delle curve
corrispondenti
Una tazza ed una ciambella sono omeomorfi.
Dalla "deformazione senza strappi" mostrata in
figura si può infatti costruire un omeomorfismo fra
i due oggetti.
La proiettività avviene mediante delle proiezioni a partire da un punto detto "centro
di proiezione".
Un esempio noto di proiettività è
l’ombra di un oggetto sottoposto a
una lampadina, fonte di luce
relativamente vicina a noi.
Notiamo che l’ombra del tavolo provocata dalla
lampadina è deformata rispetto alla figura di partenza:
mantiene solo l’allineamento dei punti delle rette e la
convessità (o la concavità) della figura
Le trasformazioni affini sono particolari proiettività che mantengono anche il
parallelismo tra rette.
Se consideriamo ancora l’esempio comune dell’ombra, un’affinità è
una trasformazione che può derivare da una fonte di luce molto
lontana, tendente all’infinito, come il sole, i cui raggi sembrano essere
paralleli tra loro.
OMBRE:
AFFINITA’ e PROIETTIVITA’
Le ombre generate dal sole sono trasformazioni affini (conservano il parallelismo).
Quelle generate da una sorgente di luce sono proiettive (conservano l’allineamento).
L’omotetia è una particolare affinità che conserva la forma delle figure e, in
particolare, la congruenza fra gli angoli; inoltre fra i segmenti esiste un rapporto
costante, detto rapporto di similitudine.
Detto k il rapporto di similitudine:
• se k > 0 l'omotetia si dice diretta.
• se k < 0 l'omotetia si dice inversa.
• se k =1 si ha l'identità;
• se k = −1 si ha la simmetria rispetto all'origine.
B’
Il triangolo rosso è stato trasformato
con l’omotetia in quello blu, un
triangolo simile. Si può applicare lo
stesso procedimento anche a figure
più complesse.
B
C’
C
A
A’
Una trasformazione che consiste in un ingrandimento
o riduzione ha come invariante globale la FORMA
delle figure.
Sono suoi invarianti :
•
L’ampiezza degli angoli
•
Il parallelismo
•
Il rapporto tra segmenti
Le isometrie sono trasformazioni che conservano le distanze
tra i punti, perciò le figure trasformate risultano congruenti a
quelle di partenza.
Sono isometrie le
traslazioni, le
rotazioni e le
simmetrie.
L' identità è la trasformazione di ogni punto del piano
associato a se stesso. In
un' identità tutti i punti sono uniti.
Trasformazioni geometriche: LE ISOMETRIE
Sono trasformazioni geometriche nelle quali la figura
trasformata rimane congruente alla figura iniziale,
conservandone sia la forma e sia la dimensione.
Le trasformazioni isometriche si ottengono mediante
movimenti rigidi delle figure, che cambiano
unicamente la loro posizione nel piano.
ISOMETRIE
Una trasformazione geometrica si chiama
isometria o congruenza quando, comunque si
scelgano due punti A e B del piano, se A’ e B’
sono i loro corrispondenti , il segmento A’B’
risulta congruente al segmento AB
LE ISOMETRIE
In matematica, e in particolare in geometria, si definisce
isometria (o trasformazione rigida) una trasformazione che
non modifica le distanze tra i punti (e, di conseguenza, le
ampiezze degli angoli).
B'
B
F‘
F
A'
A
C
C'
Le isometrie
Le principali isometrie sono:
Traslazioni
Rotazioni
Simmetria assiale
Simmetria centrale
Proprietà delle isometrie
In una isometria:
a una retta corrisponde una retta
a rette incidenti corrispondono rette incidenti
a retta parallele corrispondono rette parallele
a ogni triangolo corrisponde un triangolo ad esso congruente
ad ogni angolo corrisponde un angolo ad esso congruente
Identità
L’identità è una trasformazione
geometrica che fa corrispondere a ogni
punto il punto stesso e quindi a ogni
figura la figura stessa
Poiché a un segmento corrisponde lo stesso
segmento, l’identità è una ISOMETRIA.
Inoltre un’ identità è una trasformazione
involutoria in cui tutti gli elementi sono uniti
La traslazione
F’
F
r
La figura F con un lato
appoggiato sulla retta r è stata
spostata con un movimento
rigido ottenendo F’.
Destro
destro
Il movimento che ha portato F in F’ è una traslazione:
ogni punto di F si è spostato della stessa lunghezza
(6 cm), nella stessa direzione (parallelo ad r) e nello
stesso verso ( a destra) dando origine ad F’.
Gli elementi che caratterizzano la
traslazione sono quindi tre:
La sua lunghezza (6 cm)
La sua direzione (parallela ad r)
Il suo verso (da sinistra a destra)
Queste tre caratteristiche definiscono un
segmento orientato, chiamato vettore,
indicato con v o con AB
TRASLAZIONE
Fissato nel piano un vettore v, se a un punto
P del piano si fa corrispondere un punto P’
tale che PP’ = v si ha una corrispondenza
biunivoca tra i punti del piano, che si chiama
Traslazione di vettore v.
v
P’
P
Per individuare un vettore occorre indicare:
La sua direzione, cioè la retta a cui appartiene
Il suo verso, che indica il senso di percorrenza
La sua intensità o modulo, che rappresenta la
lunghezza del segmento AB
Teorema: la traslazione è un’isometria
Con questo teorema affermiamo che due
figure che si corrispondono in una
traslazione sono congruenti.
Inoltre la traslazione ha come caratteristiche
invarianti:
L’allineamento dei punti
La lunghezza dei segmenti
L’ampiezza degli angoli
Il parallelismo
Le direzioni
Il rapporto tra segmenti
L’orientamento dei punti del piano
La rotazione
Un’altra trasformazione che mantiene invariate
tutte le misure lineari e angolari è la
rotazione attorno ad un punto.
Per definire una rotazione è necessario che
siano dati:
1. Un punto, detto centro di rotazione
2. L’ampiezza dell’angolo di rotazione
3.
Il verso di rotazione (orario o antiorario)
ROTAZIONE
Siano dati in un piano un punto O e un angolo α di dato verso;
per ogni punto del piano, si consideri la trasformazione che
associa a un punto P il punto P’ tale che sia OP congruente
a O’P’ e l’angolo POP’ congruente ad α
Si ottiene una corrispondenza biunivoca che si dice
Rotazione
di ampiezza α intorno al centro O .
P’.
α
.
P
O
Teorema: la rotazione è un’isometria
La rotazione quindi ha le proprietà delle
isometrie ed in particolare trasforma una figura
in un’altra ad essa congruente.
Valgono le seguenti proprietà:
Il solo punto unito è il centro di rotazione
Non esistono rette unite se non quelle che si
corrispondono in una rotazione pari ad un angolo
piatto
La rotazione di ampiezza pari ad un angolo giro
coincide con la trasformazione identità
La rotazione ha come caratteristiche invarianti:
L’allineamento dei punti
La lunghezza dei segmenti
Il parallelismo
L’ampiezza degli angoli
Il rapporto tra segmenti
L’orientamento dei punti del
piano
Una Rotazione Particolare:
La Simmetria Centrale
Una rotazione di 180° attorno ad un punto C è
una simmetria centrale.
Il centro di simmetria è il centro della rotazione
Destro va in destro
Teorema: la simmetria centrale è un’isometria
Questo teorema garantisce che due figure
simmetriche rispetto ad un punto sono congruenti
SIMMETRIA
CENTRALE
Si dice simmetria centrale la trasformazione
che fa corrispondere a un punto del piano il
suo simmetrico rispetto a un dato punto 0,
detto centro della simmetria
0
P
P’
.
Simmetria centrale
Fissato il punto O
come centro di
simmetria, il punto A’
è simmetrico di A
rispetto al centro O
se O è punto medio
del segmento AA’
A’
O
A
Ogni retta passante per il centro è una retta unita,
ma non fissa perché cambia l’ordinamento dei suoi
punti
Come in ogni rotazione l’unico punto fisso è il
centro
Due segmenti, o rette che si corrispondono in una
simmetria centrale sono paralleli
La simmetria centrale è involutoria
Il Ribaltamento:
La Simmetria Assiale
Esistono situazioni in cui le figure mantengono le loro
misure, ma si ‘ribaltano’ generando figure simmetriche
rispetto ad un asse.
Definizione: si dice simmetria
assiale la trasformazione che,
data una retta r, associa ad un
punto P il suo simmetrico P’
rispetto ad r.
La retta r prende il nome di
asse di simmetria.
P'
r
M
P
Simmetria assiale
Fissata una retta r
come asse di
simmetria, il punto A’
è simmetrico di A
rispetto alla retta r
se r è l’asse del
segmento AA’
A
r
Segmenti corrispondenti sono uguali
Si conservano gli angoli
Triangoli corrispondenti sono congruenti
Sinistro destro
Teorema: la simmetria assiale è un’isometria
Questo teorema ci permette di dire che due figure che
si corrispondono in una simmetria assiale sono
congruenti.
Una retta a perpendicolare all’asse di
simmetria ha per trasformata se stessa ed è
quindi una retta unita.
Attenzione però: non è una retta di punti uniti perché ciascun punto della retta non ha come
trasformato se stesso.
Una retta a // all’asse di simmetria ha per
trasformata una retta a’ ancora // all’asse e
quindi ad a stessa.
Ogni punto dell’asse di simmetria è unito
perché gli corrisponde se stesso
Se A’ è il trasformato di A nella simmetria di
asse r, il trasformato di A’ è ancora A e quindi la
trasformazione è involutoria;
Se i vertici del triangolo ABC si susseguono in
senso orario, i loro corrispondenti A’B’C’ si
susseguono in senso antiorario e quindi
l’ordinamento dei punti non è un’invariante (è
un’isometria invertente)
Un angolo ha come asse di simmetria la sua bisettrice
Un triangolo ha un asse di simmetria solo se è isoscele
Il rombo ha due assi di simmetria (diagonali)
Il cerchio infiniti assi di simmetria
Gli invarianti della simmetria assiale sono:
L’allineamento dei punti
La lunghezza dei segmenti
Il parallelismo
Il rapporto tra segmenti
L’orientamento dei punti del piano
ISOMETRIE IN NATURA E NELL’ARTE
In natura si possono individuare forme geometriche
interpretabili assumendo come modello le trasformazioni
isometriche.
Le più frequenti sono la simmetria centrale e la
simmetria assiale, presenti in natura sia nelle forme più
elementari quali le diatomee, i protozoi e i cristalli di
neve, sia in fiori, piante, pesci, uccelli, mammiferi.
Nell’arte sin dall’antichità le trasformazioni isometriche
del piano sono state usate per creare fregi ornamentali
e pavimentazioni, per decorare soffitti e pareti di palazzi,
per disegnare tessuti, per costruire rosoni ed edifici
monumentali, realizzare statue.
La simmetria centrale e la simmetria
assiale sono involutorie
La rotazione, in generale, non è
involutoria a meno che l’angolo di
rotazione non sia un angolo piatto o
nullo. Se è piatto la rotazione è una
simmetria centrale, se è nullo la
rotazione coincide con l’identità
La traslazione non è involutoria