ELEMENTI DI STATISTICA INFERENZIALE

ELEMENTI DI STATISTICA
INFERENZIALE
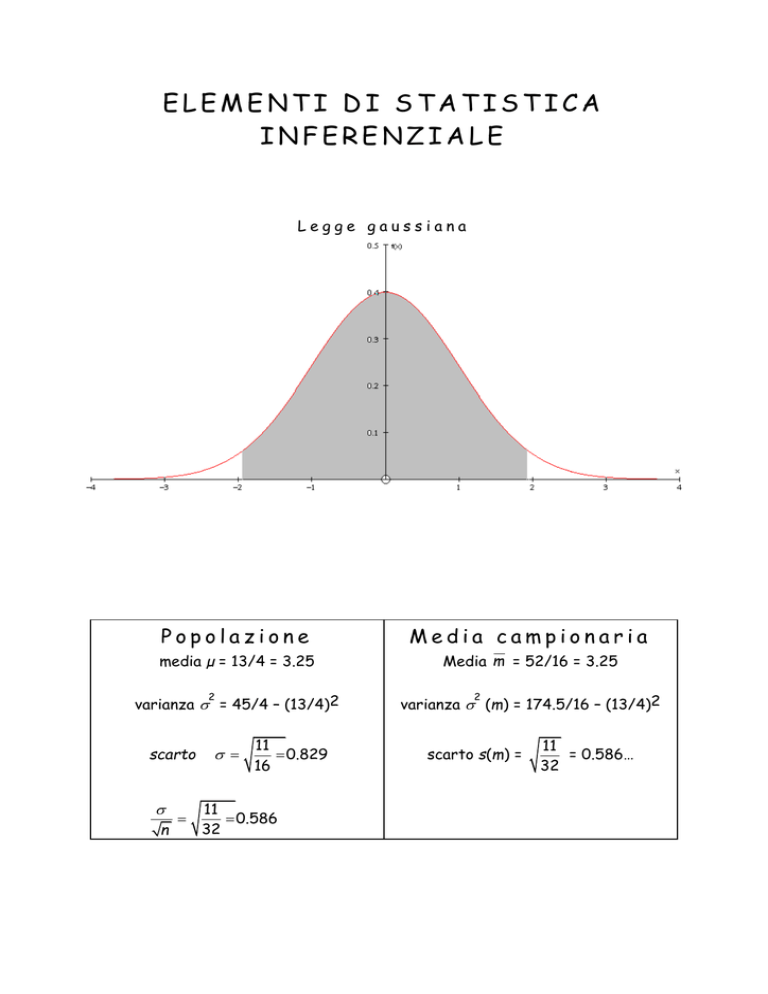
Legge gaussiana
Popolazione
Media campionaria
media µ = 13/4 = 3.25
Media m = 52/16 = 3.25
2
varianza  = 45/4 – (13/4)2
scarto

n

 
11
 0.829
16
11
 0.586
32
2
varianza  (m) = 174.5/16 – (13/4)2
scarto s(m) =
11
= 0.586…
32
-2-
ELEMENTI DI STATISTICA INFERENZIALE
La statistica inferenziale si occupa di acquisire conoscenze in condizioni di
incertezza.
Un problema tipico è quello di ricavare conoscenze circa una o più
caratteristiche di un insieme di soggetti, a partire dai valori che tali caratteristiche
hanno su una parte di essi.
La totalità dei soggetti viene detta popolazione.
Sui soggetti di una data popolazione vengono definite le caratterictiche sulle
quali si ha interesse ad avere conoscenze: possono essere variabili qualitative e
quantitative.
Ad esempio, la tabella di pag. 1 del fascicolo di Statistica Descrittiva presenta
la scelta di 9 caratteristiche: “SESSO, ALTEZZA, PESO, CORSO DI LAUREA,
NUMERO DI SCARPA, COLORE DEGLI OCCHI, COLORE DEI CAPELLI, ATTIVITÀ
SPORTIVA, TIPO DI DIPLOMA CONSEGUITO” rilevate su una popolazione
costituita da 20 studenti.
In generale una popolazione è costituita da un numero ben più elevato di soggetti:
- da alcune migliaia, a milioni o miliardi per popolazioni umane;
- possono raggiungere anche numeri più elevati per:
= prodotti industriali o dell’agricoltura;
= piante, animali, cellule, batteri, …
L’osservazione dei valori delle caratteristiche che interessano per tutti i
soggetti della popolazione (il censimento) presenta delle difficoltà:
 può non essere conveniente dal punto di vista economico, ma anche
dell’organizzazione, tecnico, … e persino legale (una ditta che produca un certo
bene può non essere autorizzata a rilevare i dati di reddito dei suoi potenziali
clienti);
 può non essere materialmente possibile: come si fa a rilevare la durata della
vita, a partire da un preciso istante, di tutte le zanzare che vivono in un grande
acquitrino? come si fa a misurare il tempo di funzionamento di lampadine
prodotte senza causare la loro distruzione?
La situazione più comune è quella nella quale non si conoscono i valori che le
caratteristiche assumono per tutti i soggetti della popolazione.
-3-
Variabili della popolazione
Tutti gli elementi di statistica descrittiva che abbiamo visto per variabili
qualitative o quantitative vengono applicati alle caratteristiche della popolazione; tali
valori spesso non sono noti: compito della statistica inferenziale è quello di avere
delle conoscenze che li riguardino.
Ad esempio, si vorrà sapere:
–
se il numero di abitanti della terra che hanno meno di 21 anni è maggiore o
minore della metà dell’intera popolazione mondiale (cioè se la mediana della
caratteristica “età” è minore o maggiore di 21 anni);
–
se un farmaco ha effetti migliori di un altro, nella popolazione italiana;
–
quanto vale l’altezza media degli italiani.
Campioni
Usualmente si cerca di dare delle risposte rilevando il valore che le
caratteristiche hanno di una parte ridotta, opportunamente scelta, della popolazione,
detta campione.
Non ci occupiamo delle raffinate tecniche che portano a campioni
rappresentativi della popolazione cioè effettivamente simili ad essa. Ci limitiamo a
quel tipo di campionamento che è alla base di esse: quello costituito dalla scelta
casuale di una dato numero n di soggetti della popolazione; occorre fare in modo che
ogni volta si fa una scelta ciascun soggetto della popolazione abbia possibilità di
essere scelto pari a quella di ogni altro.
Per darsi una rappresentazione mentale di cosa sia un campione casuale si immagini di
doverne realizzare uno di 100 elementi da una data popolazione. Si etichettano tutti i
soggetti della popolazione con un numero progressivo; si imbussolano tutti i numeri in
un’urna, e da essa si fanno 100 estrazioni, rimettendo ogni volta il numero estratto
nell’urna (così lo stesso numero può uscire più volte).
Esempio 1
Popolazione: 4 appartamenti A, B, C, D.
Caratteristica oggetto di studio: il numero di vani.
Appartamento
numero vani
A
2
B
3
C
4
D
4
-4-
Rappresentare in un istogramma la distribuzione del numero di vani della popolazione
La caratteristica X “numero dei vani” è quantitativa: ha media e scarto (ed altri
indicatori statistici: Q1, Q2, Q3, ...).
In tal senso di parla di:
media, scarto, … della popolazione.
Verrano indicate con:
 : media
 2 : varianza
 : scarto
la media, la varianza e lo scarto della caratteristica X della popolazione.
Quando non vi sono possibili confusioni fra variabili si parla semplicemente di
2
media µ varianza  e scarto  della popolazione.
Analoghe nomenclature si hanno per altri indicatori: si parla di Q1, Q2 e Q3
della popolazione. Per due caratteristiche X e Y della popolazione si parla di
covarianza cov(X,Y) oppure Γ(X, Y) o di coefficiente di correlazione ρ(X, Y), …
Calcolare media, varianza e scarto della popolazione.
xi
ni
xi ni
2
1
2
3
1
3
4
2
8
Totali
4
13
Valori della popolazione:
media µ =
varianza 2 =
xi2
xi2ni
scarto  =
-5-
Variabili campionarie
La presente tabella riporta i 16 possibili campioni di due elementi estratti dalla
popolazione dell’esempio 1.
Per ogni campione (x1, x2), riportare:
–
–
gli appartamenti che lo formano;
x  x2
la media 1
;
2
la varianza
–
lo scarto
Appartamenti
 x1
- x2 
2
;
4
 x1
- x2 
2
4
.
Campione
x1, x2
media camp.
x1  x 2
2
var. camp.
 x1
- x2 
2
4
scarto camp.
 x1
- x2 
2
4
A
A
2,
2
2.0
0.00
0.0
A
A
A
B
C
D
2,
3
2.5
0.25
0.5
B
B
B
B
A
B
C
D
3,
3,
2
3
2.5
3.0
0.25
0.00
0.5
0.0
C
C
A
B
C
C
C
D
D
D
D
D
A
B
C
D
-6-
Variabile media campionaria m
Tracciare l’istogramma della media campionaria.
2
Valore medio m , varianza  (m) e scarto (m) della media campionaria:
Valori mi
frequenze fi
2.0
1
2.5
2
3.0
5
3.5
4
4.0
4
Totali
16
mifi
2
2
mi
m i fi
1 5
Media della media campionaria m   mf
i i =
n k 1
1 5
2
Varianza della media campionaria s (m) =   mi2fi
n  k 1
Scarto della media campionaria s(m) =
1 5 2
 m fi
n  k 1 i
2

  m  =

2

  m  =

-7-
Variabile scarto campionario

Tracciare l’istogramma dello scarto campionario.
2
Valore medio s , varianza  (s) e scarto (s) dello scarto campionario:
Valori si
frequenze fi
0.0
6
0.5
6
1.0
4
Totali
16
sifi
Media dello scarto campionario s =
2
Varianza dello scarto campionario  (s) =
Scarto dello scarto campionario (s) =
2
si
2
s i fi
-8-
Confronti popolazione-campioni
(di numerosità n = 2)
Popolazione
Media campionaria
media µ = 13/4 = 3.25
Media m = 52/16 = 3.25
varianza  = 45/4 – (13/4) = 11/16
varianza  (m) = 174.5/16 – (13/4) =
5.5/16 = 11/32
2
scarto

n

2
 
2
11
 0.829
16
scarto s(m) =
11
 0.586
32
11
32
2
11
= 0.586…
32
Non si tratta di una coincidenza; con metodi matematici si può dimostrare che:
se µ e  sono rispettivamente la media e lo scarto di una popolazione, la variabile
media campionaria, per campioni di numerosità n, ha media e scarto eguali
rispettivamente a:
s(m) =
m
11
32
Se avessimo fatto campioni con molto più di due elementi?
Un importante teorema di statistica matematica (Teorema del limite centrale:
TLC) dimostra che la forma dell’istogramma che avremmo ottenuto sarebbe “molto
vicino” al grafico di una ben determinata funzione:


n



n
-9-
Tale funzione è detta normale (o gaussiana) di media µ e scarto

.
n
Il TLC afferma che l’istogramma della media campionaria ha forma normale solo
per “grandi valori” della numerosità campionaria n :
 in teoria
per n che tende ad infinito.
 in pratica
e’ sufficiente n ≥ 40, o meglio n ≥ 50.
È nota una formula che espliciti la funzione normale, al variare dei
parametri che la caratterizzano µ e

; ma poiché gli aspetti di calcolo ad essa
n
relativi sono complessi sono state compilate delle tavole numeriche che consentono di
fare i calcoli ad essa relativi.
Le tavole sono riportate nell’allegato 1; illustriamo dapprima il loro uso, poi
torniamo alle applicazioni del TLC.
Le tavole riportano i dati di una particolare curva normale (corrispondente a
determinati valori di media e scarto): ogni calcolo relativo ad altre curve normali può
essere effettuato con quella tabulata, come vedremo fra un attimo.
Se z è l’ascissa di un punto, indichiamo con Φ(z) l’area che nell’intestazione delle
tavole è annerita.
Le tavole consentono di calcolare Φ(z) nel modo che esemplifichiamo:
z = 1.37
: riga “1.3”
z = –1.03 : riga “–1.0”
colonna “7”
si legge
Φ(1.37) = 0.9147 = 91.47%
colonna “3”
si legge
Φ (–1.03) = 0.1515 = 15.15%
- 10 -
La curva normale è sempre strettamente positiva; l’area che essa sottende su
tutto l’asse reale vale 1.
Per ogni z è Φ(z) > 0, tuttavia per z > 3.9 , Φ(z) è un valore così prossimo a 0 che,
con la precisione delle quattro cifre decimali delle tavole, non si distingue da esso;
quindi nell’uso di queste tavole si assume
se z < –3.9
allora
Φ(z) = 0;
Per ogni z è Φ(z) < 1; tuttavia per alcuni di z , Φ(z) è un valore così prossimo a 1
che, con la precisione delle quattro cifre decimali delle tavole, non si distingue da
esso; quindi nell’uso di queste tavole si assume
se z > 3.9 allora
Φ(z) = 1.
Un altro uso delle tavole ci sarà particolarmente utile è il seguente:
dato un valore p (0 < p < 1) trovare z tale che l’area sottesa dalla curva nomale nelle
due “code” che formano la parte esterna all’intervallo (–z, z) abbia valore p.
Un esempio numerico chiarirà il procedimento: se p = 5% (= 0.05), l’area sottesa
nell’intervallo (–z, z) deve valere 95% (perché l’area complessiva = 100%) ; quella di
ciascuno coda 5/2 = 2.5%; quindi l’area sottesa nell’intervallo (–∞, z) deve valere
2.5+ 95 = 97.5% = 0.9750, ovvero Φ(z) = 0.975. Dalle tavole, z = 1.96.
- 11 -
Teorema del limite centrale
La probabilità P(m ≤ x) che un campione di n elementi tratto da una popolazione di
media µ e scarto , abbia valore medio minore o uguale ad un valore x è:
x - µ
P(m ≤ x) = Φ (
)
/ n
Applicazioni del TLC
Esempio 2
La popolazione dei quattro appartamenti dell’esempio 1 ha media µ = 3.25 e
scarto  = 11/32 = 0.586…
La probabilità che un campione di 100 elementi abbia media compresa fra 3.1 e
3.4 vale:
P(3.1 ≤ m ≤ 3.4) = P(m ≤ 3.4) – P(m ≤ 3.1) =
 3.4  3.25 
 3.1  3.25 
= 
  
 = Φ(2.56) – Φ(–2.56)
 11/3200 
 11/3200 
consultando le tavole ricaviamo:
P(3.1 ≤ m ≤ 3.4) = 0.9948 – 0.0052 = 0.9896
NOTA
La media campionaria ha potere “accentrante”: ben il 98.96% dei campioni (di
numerosità 100) hanno valore medio appartenente ad un intervallo di lunghezza molto
ridotta: 3.4 – 3.1 = 0.3.
Tale risultato non dipende dal numero di appartamenti di cui è formata la
popolazione, ma solo dalla sua media e dal suo scarto (oltreché dalla numerosità
campionaria).
Esempio3
Una popolazione ha media 3.25 e scarto 11/32 = 0.586… Quale deve essere la
(minima) numerosità campionaria per cui la media campionaria abbia probabilità 90%
di essere compresa nell’intervallo (3.2, 3.3)?
Ciascuna coda esterna all’intervallo cumula una probabilità (pari all’area da essa
sottesa) del 5%, ciò impone alla media campionaria che P(m ≤ 3.3) = 95%.
- 12 -
Per il TLC:

 3.3  3.25 
32n 
P(m ≤ 3.3) =  
 = 95%
    0.05
11
 11/32n 


Dalle tavole risulta:
0.05
32n
 1.65
11
(dei due valori sulle tavole, 1.64 corrispondete a 0.9495, e 1.65 che corrisponde a
0.9505 si sceglie il più grande perché evidentemente si vuole che la probabilità che la
media campionaria sia nell’intervallo (3.2, 3.3) sia del 90% o, se non è possbile questo
valore esatto “sulle tavole”, semmai un poco maggiore).
Elevando al quadrato e facendo i conti si ha
2

32n 
2
 0.05
  1.65
11


da cui n = 374.34
dovendo essere n intero si prenderà n = 375.
Problema centrale dell’inferenza statistica
Si vuole sapere se per una data popolazione è da ritenersi valida o meno una data
ipotesi H. Si considerano:
 l’ipotesi H
 i risultati sperimentali E (consistenti o no in un campione)
 la probabilità P(E | H) che avrebbe E di verificarsi se H fosse vera.
Si applica il “principio della piccola probabilità”: se P(E | H) ha un valore “piccolo”
si rifiuta che H valga in quanto la piccola probabilità P(E | H) indica che o H è falsa,
oppure si è verificato un esito sperimentale E che sarebbe raro se H fosse vera. Di
fronte all’alternativa che H sia falsa oppure che si sia relizzato un evento raro, si
sceglie la prima possibilità e si rigetta l’ipotesi H.
- 13 -
Se P(E | H) ha un valore non “piccolo” non si rifiuta H.
Nella pratica per decidere se P(E | H) è “piccola” la si confronta con un valore di
probabilità a:
 se P(E | H)  
SI RIGETTA H;
 se P(E | H)  
NON SI RIGETTA H.
Il valore  viene detto livello.
Nella pratica sono molto usati tre livelli:
 = 5%
 = 1%
 = 1‰
La scelta di  dipende dallo specifico problema che si vuole affrontare e
coinvolge aspetti che in questa sede non è possibile sviluppare.
Significato di . Il criterio di rigetto dell’ipotesi H sopra indicato non
garantisce la correttezza del risultato, ma si limita a controllarne la probabilità di
errore; un errore possibile consiste nel rifiutare H quando questa in realtà è vera;
ebbene, la sua probabilità vale proprio :
se si opera al livello
 , P(rigettare H | H è in realtà vera) = 
La probabilità dell’altro possibile errore:
P(non rigettare H | H è in realtà falsa) = 
coinvolge nozioni più complesse; il problema non viene qui affrontato. Tuttavia
esso è ampiamente sviluppato in molti problemi di statistica inferenziale e talvolta è
possibile operare in modo tale che sia  che  abbiano un valore limitato.
Test sulla media sconosciuta di una popolazione con
scarto noto.
Una popolazione abbia media sconosciuta e scarto  noto.
Sia data l’ipotesi
H
:
la media della popolazione ha valore µ
Con un campione di numerosità n, di media m, si deve decidere se rigettare o
accogliere H, ad un livello dato .
- 14 -
Si calcola un intervallo I = (µ – x, µ + x) di centro µ ed ampiezza x che contenga
la media campionaria con probabilità 1 – a; cosicche’ la probabilita’ che m non
appartenga ad I vale
.
La regola del test e’ :


se la media campionaria APPARTIENE ad I allora NON si rigetta H;
se la media campionaria NON APPARTIENE ad I allora SI RIGETTA H.
Il calcolo degli estremi dell’intervallo I è facile:
se si vuole che:
P(µ – x ≤ m ≤ µ + x) = 1 – 
basta imporre, per un ragionamento esposto poco sopra (circa i rapporti fra le
probabilità delle “code” e quella dell’intervallo centrale in una normale) che
 x -
 x 
P (m    x )   
  
  1 -  /2
 / n 
 / n 
detto z il corrispondente punto sulle tavole (z > 0) è
x
z
/ n
Ne segue:
x z

n
In conclusione, il test è il seguente:
se la media campionaria



 -z


NON appartiene all’intervallo   - z

APPARTIENE all’intervallo

,  z
 

n

 
,  z

n
n
n
allora NON si rigetta H;
allora SI RIGETTA H.
- 15 -
Esempio 4
Prima dell’esplosione di una centrale nucleare, i terreni di una certa regione
producevano quantità di grano (per una data unità di superficie) il cui valore medio
era 200 quintali con uno scarto 15. Ipotizziamo che l’effetto dell’esplosione sia tale
da non modificare il valore dello scarto. Non sappiamo se, oltre a cambiamenti nella
qualità del prodotto, vi siano stati cambiamenti anche nella quantità. Vengono scelte (a
caso) 100 unità di superificie di terreno di quella zona e di ciascuna si osservano le
quantità prodotte.
Le 100 osservazioni campionarie della produzione unitaria hanno media 196.3.
Si può ritenere, al livello del 5%, che la quantità media prodotta sia rimasta
invariata?
Si tratta di testare, al livello del 5%, l’ipotesi
H : µ = 200
Il valore z fornito dalle tavole è quello che corrisponde alla probabilità
95% + 2.5% = 97.5% = 0.9750.
tale valore e’ z = 1.96.
In corrispondenza a tale valore di z si ha:

 

,  z
I =  -z
 = (200 – 1.96
n
n

15
, 200 + 1.96
100
15
) = (197.06, 202.94).
100
Poiché la media campionaria osservata 196.3 non appartiene all’intervallo
(197.06, 202.94), l’esito del test è che si rigetta l’ipotesi che la media sia rimasta
invariata.
Si noti come, in forza della potenza del TLC, si può giungere a questa conclusione
con poche conoscenze sia sulla popolazione che sul campione:
 della popolazione basta conoscere lo scarto; ogni altra sua proprietà non
influenza il risultato;
 del campione basta conoscere il valore medio e la numerosità; gli specifici dati
campionari, così come altre sue proprietà, non influenzano il risultato.
- 16 -
Il p-value (p-valore)
Illustriamo un metodo alternativo per effettuare lo stesso test che fornisce
maggiori informazioni : il metodo del p–valore (p–value, in inglese).
Dato un campione di numerosità n e di media m, si pone x = |m – µ|.
 x  
 x 
P (m '    x )   
  

 / n 
 / n 
rappresenta la probabilità sottesa dalla sola “coda sinistra” individuata dal valore
medio del campione eseguito; se la si moltiplica per 2 si ottiene la probabilità p che un
generico campione, di pari numerosità, abbia media m' che dista dalla media µ
ipotizzata più di quanto non lo faccia m:
 x 
p  valore  2 

 / n 
Per concludere il test a livello
 si confronta p-valore con  :

se p–valore 

allora NON si rigetta H;

se p–valore 

allora SI RIGETTA H.
La conclusione di questo metodo per eseguire il test è, ovviamente, la stessa del
metodo precedente, però il p–valore dà delle maggiori informazioni:
il p-valore corrisponde a quale sarebbe il livello minimo del test che ci porterebbe a
respingere l’ipotesi H.
Esempio 5
Con i dati dell’esempio 4 si ha:
media ipotizzata µ = 200,  = 15,
n = 100,
m = 196.3,
 = 5%.
  m 
 3.7 
p-valore = 2  
  2 
  2(2.47)  2 0.0068  1.36%
 15/ 100 
 / n 
Poiche p–valore  5% si rigetta l’ipotesi che la media sia rimasta invariata. Ma tale
valore mostra che siamo abbondantemente sotto il 5% e molto vicini all’1%: i dati
campionari da noi ottenuti avrebbero una “rarità” dell’1.36% se l’ipotesi µ = 200 fosse
valida. Ciò ci può portare ad una maggiore “convinzione” nel rigettare l’ipotesi.
- 17 -
Se, ad esempio, la media riscontrata nel campione fosse stata m = 192.1,
certamente saremmo nella zona di rifiuto di H al 5%; ma il p–valore
 7.9 
p-valore = 2 
  2( 5.27)  0
 15/ 100 
avrebbe valore così piccolo da essere nullo, con l’approssimazione a quattro cifre delle
tavole. Ciò ci darebbe una convinzione molto maggiore di rigettare l’ipotesi di quanto
ne avremmo eseguendo il test col primo metodo (fatto questo che equivale
semplicemente a sapere che p–valore < 5%, senza conoscerne però il valore numerico).
Esercizio 1.
Una popolazione ha media sconosciuta e scarto 2.03.
1) Verificare l’ipotesi che la media sia 80, ad un livello del 5%, mediante un campione
di 280 elementi, di media 80.2.
2) Quanto vale il p-valore in questa situazione?
Esercizio 2.
Una popolazione ha media sconosciuta e scarto 4.11.
Si vuole che l’intervallo in cui non viene rigettata l’ipotesi
H
:
µ = 80
al livello dell’1%, abbia lunghezza pari a 1.5.
1) Qual è la minima numerosità campionaria n per cui ciò accade?
2) Il valore di n dipende dal valore ipotizzato 80 della media µ della popolazione?
- 18 -
Indipendenza di due variabili
In molti casi sorge il problema di sapere se due variabili sono indipendenti oppure no.
Ad esempio si vorrà sapere se è vero o no che:
–
chi fuma ha un rischio di tumori (polmonari e non solo) maggiore (o molto
maggiore) di chi non fuma;
–
chi usa il casco nei mezzi a due ruote ha un rischio di traumi cranici minore
(molto minore) di chi non lo mette;
–
chi usa precauzioni igieniche ha rischi minori (o molto minori) di insorgenza di
certe malattie di chi non le usa;
–
vi sia dipendenza fra la presenza di una data sostanza in un certo ambiente e le
possibilità di vita di certe piante o di certi animali in esso viventi.
Per lo studio dell’effetto combinato di due variabili X e Y su una popolazione, si
dovrà prendere in considerazione per ogni suo soggetto la coppia “bivariata” di valori
(x, y) che esse hanno su di lui (così come nella tabella di pag. 2 ogni soggetto individua
i nove valori che le variabili ivi definite assumono su di lui).
Se si potesse fare il censimento dei valori della coppia (X, Y) allora il problema
della indipendenza delle variabili X e Y non sarebbe di inferenza statistica (non ci
sarebbero problemi di problemi di conoscenza in condizione di incertezza) ma si
tratterebbe di trovare un “buon indice” capace di misurare l’indipendenza delle
variabili (ad esempio, per variabili quantitative potrebbe venire in mente di utilizzare
il coefficiente ρ(X, Y), calcolato per tutti i soggetti della popolazione, o altri indici).
Il problema inferenziale nasce, anche in questo caso, dal poter disporre di sole
osservazioni campionarie.
- 19 -
Il test
2 d i i n d i p e n d e n z a
A rigore si può applicare solo per due variabili qualitative.
Il suo principio di funzionamento è ancora quello della “piccola probabilità”;
schematicamente:
–
si fa l’ipotesi H
–
si sceglie un livello
–
si fanno le osservazioni E;
–
si la probabilità P(E | H) che esse avrebbero se H fosse vera;
–
si confronta tale probabilità con il livello

se P(E | H) 

se P(E | H) 

:
le variabili X e Y sono indipendenti
 del test (comunemente uno dei valori 5%, 1%, 5‰);
:
SI RIGETTA H;
NON SI RIGETTA H.
Si vuole valutare se vi sia o meno indipenenza fra le due variabili
X settore lavorativo, ripartita nei 4 settori: X1 :
X2 :
e Y tipo di lavoro, ripartita in
Agricoltura
Industria
X3 :
X4 :
Servizi commerciali
Y1 :
Dipendenti
Y2 :
Indipendenti
Servizi non commerciabili
I dati di un campione di 23˙132 osservazioni sono riportati in tabella:
X Settore lavorativo\Y lavoro
Indipendenti
Totale
751
1˙545
2˙296
X2: Industria
5˙544
1˙319
6˙863
X3: Servizi commerciali
5˙255
4˙503
9˙758
X4: Servizi non commerciabili
4˙215
0
4˙215
15˙765
7˙367
23˙132
X1: Agricoltura
Totale
Dipendenti
- 20 -
Il lettore cerchi ora di pronunciarsi, ad un livello percettivo, sui quesiti seguenti:
–
i dati riportati segnalano, a suo giudizio, dipendenza o indipenenza fra X e Y?
–
se dipendenti, si ritiene che sia una dipendenza molto forte o piuttosto debole?
esprimetela con una misura percentuale (0: indipendenza, 100: dipendenza
massima)
–
quale grado di convinzione avete sulla validità delle due affermazioni
precedenti? esprimetelo con una misura percentuale (0: totale incertezza, 100:
sicurezza assoluta).
Proseguiamo nella esposizione del test
2 di indipendenza.
L’indipendenza o la dipendenza delle variabili è un fatto che è collegato solo ai valori
“interni” della tabella, quelli che sono stati omessi nella tabella seguente:
X Settore lavorativo\Y lavoro
Dipendenti
Indipendenti
Totale
X1: Agricoltura
2˙296
X2: Industria
6˙863
X3: Servizi commerciali
9˙758
X4: Servizi non commerciabili
4˙215
Totale
15˙765
7˙367
23˙132
Per ciascuna delle caselle bianche della tabella, siamo in grado di determinare un
valore attorno al quale dovrebbero avvicinarsi le frequenze osservate se
effettivamente le variabili fossero indipendenti:
se due variabili sono indipendenti i profili riga sono tutti uguali, lo stesso i profili
colonna.
Detto in altre parole i 2˙296 lavoratori del settore “Agricoltura” si dovrebbero
ripartire in “Dipendenti” e “Indipendenti” nelle stesse proporzioni con cui si
ripartiscono tutti i 23˙132 soggetti osservati nel campione.
Questa proporzionalità dà luogo alla tabella delle così dette “frequenze
teoriche” (“teoriche”: nell’ipotesi che la variabili siano effetivamente indipendenti);
essa è così strutturata:
si fa una tabella che abbia la stessa riga e colonna marginali della precedente, poi
si calcolano le frequenze teoriche ti previste in ogni casella in modo da rendere tutte
le righe (e, necessariamente, anche tutte le colonne) proporzionali fra loro.
- 21 -
X Settore lavorativo\Y lavoro
Dipendenti
Indipendenti
Totale
X1: Agricoltura
t1
t2
2˙296
X2: Industria
t2
t3
6˙863
X3: Servizi commerciali
t4
t5
9˙758
X4: Servizi non commerciabili
t6
t7
4˙215
15˙765
7˙367
23˙132
Totale
Ovviamente le frequenze teoriche sono tante quanto è il numero k delle caselle
interne della tabella; nel nostro caso è k = 8.
Le frequenze teoriche ti sono calcolabili con proporzioni del tipo:
t1 : 2˙296 = 15˙765 : 23˙132
t1 =
2 296 15 765
= 1 564.8
23 132
t4 : 6˙863 = 7˙367 : 23˙132
t4 =
6 863 7 367
= 2 185.7
23 132
Le frequenze teoriche non sono, in generale, numeri interi. Soprattutto quando
siano valori non troppo grandi è consigliabile di approssimarle con più di un decimale.
Nel caso presente, in cui hanno valore elevato, assumiamo un decimale.
La regola per il calcolo delle frequenze teoriche è molto semplice:
Il valore della frequenza teorica da riportare in una data casella si ottiene
moltiplicando fra loro i due totali della riga e della colonna cui la casella appartiene,
poi dividendo per il totale generale delle tabella.
In tal modo si ottiene la tabella delle frequenze teoriche
X Settore lavorativo\Y lavoro
Dipendenti
Indipendenti
Totale
X1: Agricoltura
1˙564.8
731.2
2˙296
X2: Industria
4˙677.3
2˙185.7
6˙863
X3: Servizi commerciali
6˙650.3
3˙107.7
9˙758
X4: Servizi non commerciabili
2˙872.6
1˙342.4
4˙215
Totale
15˙765
7˙367
23˙132
- 22 -
Le frequenze dei dati osservati vengono chiamate frequenze osservate; vengono
indicate con fi indiciandole con lo stesso ordine, in modo che le frequenze osservate
fi e quelle teoriche ti si corrispondano nelle rispettive tabelle.
Il test procede misurando la discrepanza fra le frequenze osservate e quelle
teoriche, prima casella per casella, poi quella complessiva.
La discrepanza fra fi e ti di una data casella è misurata in due fasi:

dapprima, con le stesse motivazioni che abbiamo già utilizzato nella definizione
di varianza e di scarto, si considera la differenza quadratica “assoluta”
2
(fi – ti) ;

poi si tiene conto che tale valore ha maggiore o minore importanza a seconda
del valore che ci aspettiamo in quella casella (così come l’errore assoluto di 1
cm nella misura di una lunghezza ha un peso in relazione alla lunghezza di 1
metro, ma ha peso molto minore in relazione ad una lunghezza di vari
chilometri, e quindi si considera l’errore relativo: (1 cm) /(vari chilometri)
assumendo questo come “precisione della misura) esprimendo la discrepanza fra
fi e ti di una data casella con la differenza quadratica “relativa”:
2
(
f

t
)
i2  i i
ti
Si noti che al denominatore è posta la frequenza teorica!
La discrepanza complessiva fra le frequenze osservate e quelle teoriche è
misurata dall’indice:
(fi  ti )2
 
ti
i 1
2
k
dove k il numero delle caselle “interne” alla tabella.
- 23 -
Nel caso esemplificato si ha:
(751-1564.8)2 (1545-731.2)2 (5544-4677.3)2
 =
+
+
+
1564.8
731.2
4677.3
(1319-2185.7)2 (5255-6650.3)2 (4503-3107.7)2
+
+
+
2185.7
6650.3
3107.7
(4215-2872.6)2 (0-1342.4)2

 4722.17
2872.6
1342.4
2
Se si fanno i calcoli con il valore esatto (frazionario) delle ti si ottiene
2 = 4855.94
2 assume valori prossimi a 0 quando le frequenze osservate sono “vicine” a
quelle teoriche (in effeti, 2 = 0 se e solo se fi = ti per ogni i). Viceversa elevati valori
di 2 indicano che vi è discrepanza fra frequene osservate e le corrispondenti
teoriche. Se 2 è troppo grande (o meglio, se è così grande da rendere inferiore al
L’indice
livello prescelto la probabilità dei dati osservati) si rigetterà l’ipotesi.
Ne segue che le zone di rifiuto dell’ipotesi (di indipendenza delle variabili) di questo
test sono del tipo:
2 > c
per una opportuna costante c. Ciò corrisponde a dire (si guardino le tavole della
distribuzione 2) che le zone di rifiuto sono delle “code destre”, cioè corrispondono
alle ascisse dei punti appartenenti alla regione annerita nella figura allegata alle
tavole.
Ora illustriamo come calcolare c in modo da tener conto degli aspetti probabilistici
legati al livello del test.
Come per la media campionaria col TLC, vi è un teorema di statistica matematica che
ci consente di valutare le probabilità che
2 assuma determinati valori.
Anche in questo caso:
–
le formule relative, troppo complesse per essere trattate in questa sede,
possono essere evitate ricorrendo ad opportune tavole che danno la distribuzione di
2; le tavole sono riportate nell’allegato 2;
–
la distribuzione fornita dalle tavole ha bisogno, in teoria, che n   ; in
- 24 -
pratica essa è buona quando TUTTE le frequenze TEORICHE (teoriche! non quelle
osservate) hanno valore
ti ≥ 5 o meglio ancora ti ≥ 10
per cui si sconsiglia di utilizzare questo test se anche solo per qualcuna delle
frequenze teorica avviene che ti < 5.
La distribuzione di 2 fornita dalle tavole dipende da un parametro chiamato numero
dei gradi di libertà. Questo viene indicato con . Il suo valore dipende dal numero di
righe e di colonne della “parte interna” della tabella (quella comprendente le caselle in
corrispondenza delle quali sono calcolate le frequenze teoriche). Ad esempio, nella
tabella da noi esemplificata la “parte interna” ha 4 righe (corrispondendi ai 4 settori
di lavoro) e 2 colonne (corrispondenti alla classificazione della variabile Y in
“Dipendenti” e “Indipendenti”). Il numero dei gradi di libertà è definito da:
 = (numero di righe – 1) (numero di colonne – 1).
Nel caso indicato,  = (4 – 1) (2 – 1) = 3 · 1 = 3.
Nelle tavole, la prima colonna corrisponde al numero dei gradi di libertà.
Si considera la riga individuata da  e la colonna individuata dal livello
all’intersezione di esse si trova il valore “critico” c, si confronta
se
se
,
2
 con c:
2 ≥ c SI RIGETTA H;
2 < c NON SI RIGETTA H.
Nel caso da noi illustrato, si ha:
a = 5%
Poiché
2 = 4˙855.94…
=3
dalle tavole: c = 7.815
2 = 4˙855.94… > c = 7.815, si rigetta H (al livello del 5%).
Si noti che, in questo caso, il valore di  2 è così elevato da superare i valori
critici riportati nella tabella corrispondenti ai livelli dell’1% e del 5‰.
Esercizio. 762 animaletti di una data specie, che vivono nelle acque di un lago, sono
stati classificati a seconda del sesso e della profondità (moderata, media o elevata) a
cui sono stati prelevati.
I risultati sono riportati nella seguente tabella:
- 25 -
Maschi
Femmine
Totale
Valutare, col test
Profondità Profondità Profondità
moderata
media
elevata
220
112
56
202
130
42
422
242
98
Totale
388
374
762
2 al livello del 5%, se si possa ritenere che vi sia indipendenza
fra il sesso e la profondità.
Esercizio 3.
I mille individui di un campione sono stati classificati secondo il sesso e secondo
il fatto di essere o meno daltonici:
Normali
Daltonici
Totali
Maschio
442
38
480
Femmina
514
6
520
Totali
956
44
1˙000
Valutare, mediante il test 2, ad un livello del 5%, se si può ritenere che l’essere o
meno daltonici sia un fenomeno indipendente dal sesso.
Esercizio 4.
Un vaccino è stato somministrato ad alcune persone scelte a caso fra un folto
gruppo di volontari. Le successive osservazioni hanno fornito i seguenti risultati:
Vaccinati
Non vaccinati
Totali
Infettati
56
272
328
Non infettati
6˙759
11˙396
18˙155
Totali
6˙815
11˙668
18˙483
Questi dati sono compatibili con l'ipotesi che il vaccino non abbia effetto, ovvero
che l'essere o meno vaccinati (con quel vaccino) non influenzi il fatto di essere o meno
infettati?
- 26 -
ALLEGATO 1 : TAVOLE NORMALE STANDARDIZZATA
- 27 -
ALLEGATO 2 : TAVOLE CHI QUADRO
(2)