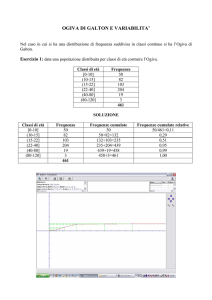
Grafici delle distribuzioni di frequenza
L’osservazione del grafico può far notare irregolarità o
comportamenti
anomali
non
direttamente
osservabili sui dati; ad esempio errori di
misurazione
1) Diagramma circolare; in questo diagramma le
frequenze percentuali sono rappresentate da settori
circolari aventi ampiezze proporzionali alle frequenze
stesse; indicando con f la frequenza percentuale e
con g l'ampiezza in gradi, si ha
f : 100 = g : 360 °
1
Esempio
Numero di studenti iscritti ai vari anni di corso di un
istituto superiore (frequenze assolute) e le
corrispondenti frequenze percentuali.
Studenti iscritti ai diversi anni di corso
freq.
assoluta
187
freq. percentuale
classi
seconde
classi terze
214
21.75%
225
22.87%
classi quarte
176
17.89%
classi quinte
182
18.50%
Totale
984
100.01%
classi prime
quinte 18%
prim e 19%
19.00%
qua rte 18%
s e conde 22%
te rze 23%
2
Grafici delle distribuzioni di frequenza
2) Diagramma a barre; Per ciascuna classe si
disegna un rettangolo avente base di ampiezza
costante e altezza uguale alla frequenza di classe; i
rettangoli di solito non sono adiacenti e sono
equidistanti fra loro.
12
Diagramma relativo alla
distribuzione di particelle
cosmiche
10
8
6
4
2
0
0
1
2
3
4
5
6
7
8
3
Grafici delle distribuzioni di frequenza
3) Istogrammi: un istogramma consiste in un insieme di
rettangoli adiacenti, con base sull’asse orizzontale; le
basi sono gli intervalli che definiscono le classi. Se le
classi hanno tutte la stessa ampiezza le altezze dei
rettangoli sono uguali, o proporzionali, alle
corrispondenti frequenze assolute.
Classe
Valori centrali
Freq. assoluta
5≤x<9
9 ≤ x < 13
13 ≤ x < 17
17 ≤ x < 21
21 ≤ x < 25
25 ≤ x < 29
29 ≤ x < 33
Totale
7
11
15
19
23
27
31
3
10
14
25
17
9
2
80
Esempio 2:
30
25
20
15
10
5
0
0
3
7
11
15
19
23
27
31
35
4
Applicazione
Tabella delle lunghezze di 40 sbarrette metalliche;
costruire una distribuzione di frequenza assoluta e
disegnare il relativo istogramma.
138
146
168
146
161
164
158
126
173
145
150
140
138
142
135
132
147
176
147
142
14
12
10
144
136
163
135
150
125
148
119
153
156
149
152
154
140
145
157
144
165
135
128
118 ≤ x ≤ 126
3
127 ≤ x ≤ 135
5
136 ≤ x ≤ 144
9
145 ≤ x ≤ 153
12
154 ≤ x ≤ 162
5
163 ≤ x ≤ 171
4
172 ≤ x ≤ 180
2
8
6
4
2
0
113
122
131
140
149
158
167
176
185
5
Applicazione
Aree dei continenti; disegniamo il grafico dei dati con un
diagramma a barre e con un diagramma circolare.
Europa
Asia
Africa
America Nord
10368
45078
30209
24203
America Sud
Oceania
8522
Antartide
14108
Europa
8
Europa
7
Asia
Europa
6
Anta rtide
Africa
5
America Sett. e Centr.
4
Oceania
2
0
0.5
1
1.5
2
2.5
3
Area (migliaia di Kmq)
Africa
Ame rica Sett. e
Ce ntr.
Antartide
1
Asia
Oce a nia
Ame rica
Me rid.
America Merid.
3
0
17855
3.5
4
4.5
5
x 10
4
6
EXCEL: ANALISI DATI
STRUMENTI DI ANALISI è un insieme di strumenti di
analisi dei dati che consente di ridurre i passaggi necessari
allo sviluppo di complesse analisi statistiche. Forniti i dati e i
parametri per ciascuna analisi, lo strumento utilizzerà le
funzioni macro statistiche appropriate, visualizzando i
risultati in una tabella di output.
Per visualizzare un elenco degli strumenti di analisi:
scegliere Analisi dati dal menu Strumenti. Se tale comando
non è visualizzato, dal menu Strumenti selezionare
Aggiunte… e scegliere Analisi dati.
7
EXCEL: Strumento di analisi Istogramma
Consente di calcolare le frequenze individuali e cumulative per
un intervallo di celle e di classi di dati.
Opzioni della finestra di dialogo Istogramma:
•intervallo di input: immettere il riferimento di cella per
l’intervallo di dati da analizzare
•intervallo di classe (facoltativo): immettere un intervallo di
celle contenente un insieme di valori limite che definiscano gli
intervalli delle classi
•intervallo di output: immettere il riferimento della cella
superiore sinistra della tabella di output
Esercizio: esercizi_lab1 - Esercizio 5-6
8
Indici di posizione e di dispersione
Le statistiche sono indici numerici utili per descrivere
i dati e la loro distribuzione; studieremo media,
moda, varianza e scarto quadratico medio o
deviazione standard.
Si definisce media aritmetica o media campionaria di n
dati x1 , x 2 , ..... , x n la quantità:
1 n
x=
xi
∑
n
i =1
Per ogni valore xi della variabile x si definisce lo scarto dalla
media si = xi − x che indica il grado di scostamento del singolo
valore xi dalla media .
9
Indici di posizione e di dispersione
Si definisce moda ~x di un insieme di n dati il valore o
la classe a cui corrisponde la massima frequenza
assoluta.
La moda è per lo più utilizzata quando si trattano dati di tipo
qualitativo, per i quali non è possibile calcolare la media.
•
Nell'insieme di dati: 3, 3, 5, 4, 7, 7, 7, 9, 2, 1 ho
media: 4.8 e moda: 7
Media e moda sono detti indici di posizione o indici di
tendenza centrale, perché descrivono attorno a quale
valore è centrato l'insieme di dati.
10
Indici di posizione e di dispersione
Si definisce varianza, o anche varianza campionaria,
la quantità:
2
1 n
s2 =
(
xi − x)
∑
n −1
i =1
Si definisce scarto quadratico
medio o deviazione standard la
radice quadrata della varianza.
∑(
)
2
1 n
s=
xi − x
n −1 i=1
Varianza e scarto quadratico medio sono detti indici di
dispersione o indici di variabilità, perché misurano la
dispersione dei dati attorno alla media
11
Applicazione
I seguenti dati sono i tempi di esecuzione di una certa
operazione misurati in minuti: 0.6, 1.2, 0.9, 1.0, 0.6, 0.8
Calcoliamo la varianza e la deviazione standard.
xi
xi − x
(x i − x )
0.6
−0.25
0.0625
1.2
0.35
0.1225
0.9
0.05
0.0025
1.0
0.15
0.0225
0.2750
s =
= 0.055 minuti2
5
0.6
−0.25
0.0625
s = 0.055 ≅ 0.23 minuti
0.8
−0.05
0.0025
totale
2
x = 0 .85
2
0.2750
12
Applicazione
Voti in trentesimi riportati da 25 studenti in un esame:
quali studenti si discostano dal voto medio per più di
una volta lo scarto quadratico medio?
numero studente
1
2
3
4
5
6
7
8
9
10
11
12
13
voto
15
17
27
25
29
14
16
25
27
18
10
15
27
numero studente
voto
x = 21.40
14
15
16
17
18
19
20
21
22
23
24
25
28
19
14
30
21
17
24
29
20
13
30
25
s = 6.21
x − s = 15.19 x + s = 27.61
11
voti
non
appartengono
all'intervallo [−s ,+s], ossia si
discostano dalla media per più di una
volta lo scarto quadratico medio.
13
Applicazione
Per rappresentare la situazione può essere utile un diagramma nel
piano cartesiano con il quale si individuano più facilmente gli
studenti che rientrano nella fascia delimitata dai valori −s ,+s.
35
xm e d +2s
30
xm e d +s
25
20
15
10
5
xm e d
xm e d -s
xm e d -2s
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Esercizi: esercizi_lab1 - Esercizio 1
14
Forma di una distribuzione
Distribuzioni di frequenza: forma a campana.
La distribuzione dei dati è simmetrica rispetto a una linea
verticale (figura 1); i dati di questo tipo si dicono normali.
Se la distribuzione dei dati non è perfettamente simmetrica,
i dati si dicono approssimativamente normali (figura 2).
40
40
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Forma di una distribuzione
Una distribuzione asimmetrica può avere una
“coda” a destra (distribuzione obliqua a destra o con
asimmetria positiva, figura 3) o a sinistra
(distribuzione obliqua a sinistra o con asimmetria
negativa, figura 4).
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
16
Forma di una distribuzione
La media e lo scarto quadratico medio forniscono
importanti informazioni sulla distribuzione dei dati
infatti
se
la
distribuzione
dei
dati
è
approssimativamente normale con media x e scarto
quadratico medio s, allora vale la seguente regola: :
1 − circa il 68% dei dati è compreso fra
x−s e x+s
2 − circa il 95% dei dati è compreso fra
x − 2s
3 − circa il 99.7% dei dati è compreso fra
e
x + 2s
x − 3s e x + 3s
17
Applicazione
Per i dati dell’esempio 2 si possono calcolare i
seguenti valori per la media e lo scarto quadratico:
s 2 = 32.00
s = 5.66
La regola empirica afferma che circa il 68% dei dati cade in
x = 18 . 89
(x − s = 13.23, x + s = 24.55)
Verifica:
80−28=52 dati in
(13.23-24.55),
cioè il
52
⋅ 100 % =
80
= 65% dei dati.
15.8 26.4 17.3 11.2 23.9 24.8 18.7 13.9
22.7
9.8
6.2
9.0
13.2
14.7 17.5 26.1 12.8 28.6 17.6 23.7
26.8 22.7 18.0 20.5 11.0 20.9 15.5 19.4 16.7 10.7
19.1 15.2 22.9 26.6 20.4 21.4 19.2 21.6 16.9 19.0
18.5 23.0 24.6 20.1 16.2 18.0
7.7
13.5 23.5 14.5
14.4 29.6 19.4 17.0 20.8 24.3 22.5 24.6 18.4 18.1
8.3
21.9 12.3 22.3 13.3 11.8 19.3 20.0 25.7 31.8
25.9 10.5 15.9 27.5 18.1 17.9
9.4 24.1 20.1 28.5
18
EXCEL: Strumento di analisi Statistica descrittiva
Opzioni della finestra di dialogo Statistica descrittiva:
• intervallo di input: immettere il riferimento di cella per
l’intervallo di dati da analizzare
• intervallo di output: immettere il riferimento della cella
superiore sinistra della tabella di output
• Riepilogo statistiche: genera una tabella di output con
le seguenti statistiche:Media, Errore standard (della
media), Mediana, Moda, Dev. Standard, Varianza,
Curtosi, Asimmetria, Intervallo, Min, Max, Somma
Conteggio.
Esercizi:
esercizi_lab3
esercizi_lab2 - Esercizi 1-2-3
19