media formula 2

Integrale Definito - Calcolo delle
Aree
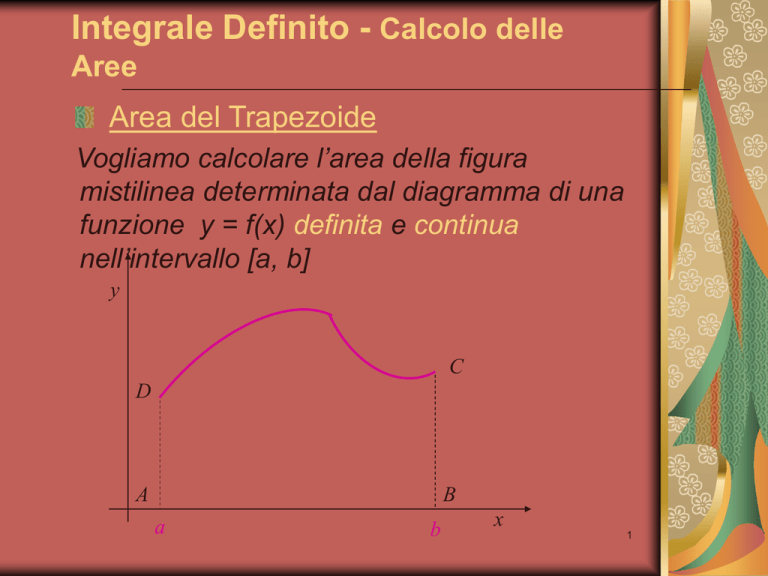
Area del Trapezoide
Vogliamo calcolare l’area della figura
mistilinea determinata dal diagramma di una
funzione y = f(x) definita e continua
nell’intervallo [a, b]
y
C
D
A
B
a
b
x
1
Possiamo determinare l’area
approssimandola con dei rettangoli inscritti e
dei rettangoli circoscritti
Utilizzando lo stesso metodo usato per il
Dividendo in n parti
cerchio.
l’intervallo [a, b], avremo n
rettangoli di base
h = (b – a)/n
y
C
Indichiamo con
sn =  areaRett.inscritti
D
L’area del plurirettangolo
B inscritto
A
a
b
x
2
Analogamente possiamo determinare l’area
Sn del plurirettangolo circoscritto
Indichiamo con
Sn =  areaRett.circoscritti
y
C
D
A
B
a
b
x
L’area S del trapezoide sarà sempre compresa tra sn e Sn
 areaRett.inscritti  S   areaRett.circoscritti
3
Aumentando il numero dei rettangoli
l’approssimazione di S sarà sempre più
precisa.
Considerando un numero di rettangolini via via crescente
avremo due successioni di aree di
plurirettangoli inscritti
s1, s2, … sn, … e di
plurirettangoli circoscritti
S1, S2, …Sn,…
che convergono all’area del trapezoide ABCD
Teorema 1. Se y = f(x) è continua e positiva in [a, b], allora le
successioni delle aree s1, s2, … sn, … e S1, S2, …Sn,…
convergono allo stesso limite S uguale all’area del trapezoide
ABCD
lim sn  lim Sn  S
n
n
4
Integrale Definito - Calcolo delle Aree
Possiamo finalmente giungere al concetto d’integrale definito
Integrale Definito
Data la funzione y=f(x) definita e continua in [a,
b], dopo aver diviso l’intervallo in n parti, indichiamo
con
mi = min f(x) e con Mi = max f(x) nell’intervallino
i-esimo di ampiezza h
y
C
Mi
D
sn =AreaPluriRettinscr. =  mih
Sn =AreaPluriRettcirco. =  Mih
mi
A
a
i
h
ARettcirco. = Mih
ARettinscr. = mih
B
b
x
5
Integrale Definito - Calcolo delle Aree
Allora,indicando con f(i ) il valore della funzione in un punto
qualsiasi dell’intervallo i-esimo,
tenendo conto del teorema del confronto e del teorema 1
mi  f ( i )  M i
 m  f ( )   M
y
i
Mi
D
C
f(i )
 m  h  f ( )  h   M  h
i
n 
A
i
i
n
B
i
i
lim  mi  h  lim  M i  h S
mi
a
i
b
x
avremo che:
mi  h  lim  M i  h  lim  f ( i )  h S

n
n
n
lim
6
Integrale Definito - Calcolo delle Aree
Allora, possiamo dare la seguente definizione:
Def. Data la funzione y=f(x) definita e continua in
[a, b], si dice Integrale definito di f(x) relativo
all’intervallo [a, b] il limite
mi  h  lim  M i  h  lim  f ( i )  h S

n
n
n
lim
b
e si indica con

f ( x )dx
a
7
Integrale Definito - Proprietà
Proprietà dell’Integrale definito
b
a)
a
a
 f ( x)dx   f ( x)dx
a
 f ( x)dx  0
b)
b
a
Proprietà di linearità
c)
d)
b
b
a
a
 kf ( x)dx  k  f ( x)dx
b
b
b
a
a
a
  f ( x)  g ( x)dx   f ( x)dx   g ( x)dx
Proprietà di additività
e)
b
c
b
a
a
c
 f ( x)dx   f ( x)dx   f ( x )dx
8
Integrale Definito - Proprietà
Teorema della Media
Se y = f(x) è una funzione continua nell’intervallo
chiuso e limitato [a, b] allora esiste almeno un punto
c(a, b) tale che:
b
 f ( x)dx  (b  a ) f (c)
a
y
f(c)
C Cioè esiste sempre un
f(c)
rettangolo di base AB e altezza
uguale a f(c) avente la stessa
area del rettangoloide.
D
A
c
a
c
B
b
x
9
Integrale Definito - Calcolo dell’integrale
Funzione Primitiva
Il calcolo dell’integrale come lim  è
estremamente complesso e per nulla
conveniente, occorre allora trovare un altro
sistema per calcolarlo.
abbiamo bisogno di vedere il concetto di
primitiva e il teorema di Torricelli-Barrow
Il problema del calcolo della Primitiva è il problema
inverso del calcolo della derivata:
calcolare la primitiva significa:
data la derivata f(x) di una certa funzione non nota F(x)
calcolare la funzione y=F(x),
quindi F’(x) = f(x)
10
Integrale Definito - Calcolo dell’integrale
Derivata
?
F(x)
f(x)
Primitiva
Def. Diremo che F(x) è una primitiva della funzione
y=f(x) in [a, b]
sse
F(x) è derivabile in [a, b] e risulta:
F’(x) = f(x)
 x [a, b]
11
Integrale Definito - Calcolo dell’integrale
Primitive, alcuni esempi:
Primitiva (2x) = x2
--- infatti  D(x2) = 2x
Primitiva (cosx) = senx
= cosx
Primitiva (1/x) = lnx
--- infatti  D(senx)
--- infatti  D(lnx) = 1/x
Primitiva (1/cos2x) = tgx --- infatti  D(tgx) =
1/cos2x Osserviamo anche che:
D(x2-1) = 2x --- quindi  Primitiva (2x) = x2 –1
D(x2+5) = 2x --- quindi  Primitiva (2x) = x2 +5
D(x2+a) = 2x --- quindi  Primitiva (2x) = x2 +a
12
Integrale Definito - Calcolo dell’integrale
Oss
Se F(x) è una primitiva di f(x) allora
anche
G(x) = F(x) + c  c R è una primitiva
di f(x)
e viceversa
se F(x) e G(x) sono primitive di f(x) allora
G(x) = F(x) + c
Allora una funzione ammette infinite primitive che
differiscono per una costante reale e costituiscono una
famiglia di infinite curve ottenibili per traslazione
secondo l’asse y.
13
Integrale Definito - Calcolo dell’integrale
Def
L’insieme di tutte le primitive di una funzione y = f(x) si
chiama
INTEGRALE INDEFINITO di f(x),
si indica col simbolo:
 f ( x)dx
e si legge “Integrale indefinito di f(x) in dx”
14
Integrale Definito - Calcolo dell’integrale
Allora, riprendendo gli esempi precedenti

Dx

 f ( x)dx  Pr imitive f ( x)
2


2
xdx

Pr
imitive
(
2
x
)

x
c

 cos xdx  Pr imitive(cos x)  sin x  c
D  f ( x )dx  f ( x )

1
 1 
dx

Pr
imitive
   ln x  c
 x 
 x 
Dln x  c  

 1 
dx

Pr
imitive

  tgx  c
 cos 2 x 
2
 cos x 
Dtgx  c  
1
2

 c  2x
Dsin x  c   cos x
1
x
1
cos 2 x
15
Integrale Definito - Proprietà
Teor. di Torricelli- Barrow (funzione
Integrale)
Sia y = f(x) funz. continua nell’intervallo [a, b],
consideriamo un punto x variabile (a, b)
x
Al variare di x l’integrale
 f (t )dt
assume valori variabili, cioè è unaa funzione di x che
y indicheremo con F(x) e chiameremo funzione integrale
f(x)
C
D
x
F ( x )   f (t )dt
a
A
x
a
B
b
x
16
Integrale Definito - Proprietà
In particolare
a
b
Se x = a F ( a )   f (t )dt  0
se x = b F (b)   f (t )dt
a
a
Avremo allora il seguente
Teor. di Torricelli- Barrow
Se y = f(x) è continua in x[a, b] allora la
funzione integrale
F ( x )  f (t )dt

a
è derivabile e risulta: F’(x) = f(x); cioè F(x) è
una primitiva di f(x).
17
Integrale Definito - Proprietà
Calcolo dell’Integrale Definito
Formula di Newton-Leibniz
Finalmente possiamo calcolare l’integrale definito
b
 f (t )dt  area trapezoide
a
Considerando la funzione integrale avremo:
a
x

f (t )dt  G ( x )  c
a
Da cui c =  G(a)
e per x = a
x


f (t )dt  G ( a )  c  0
a
f (t )dt  G ( x )  c  G ( x )  G ( a )
a
b
e per x = b

a
f (t )dt  G(b)  G( a )  G( x )a
b
18
Integrale Definito - Proprietà
Teorema fondamentale del calcolo
integrale
L’integrale definito di una funzione continua y=f(x),
calcolato nell’intervallo [a, b], è uguale alla differenza
tra i valori che una qualunque primitiva di f(x) assume
agli estremi superiore e inferiore dell’intervallo
d’integrazione.
b
 f (t )dt  G(b)  G(a)  G( x)
b
a
a
19