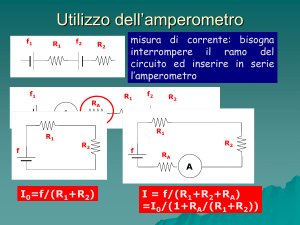
Università degli Studi di Bologna
Seconda Facoltà di Ingegneria - Sede di Cesena
C.d.L. in Ingegneria Elettronica e delle Telecomunicazioni
Misura della caratteristica statica di un carico
ohmico con metodo volt-amperometrico
Misure elettroniche L-A (prof. P. A. Traverso)
Anno Accademico 2008/09
Data esecuzione: 25 novembre 2008
Gruppo IX
Marco
Alessandrini
Alessandro
Callozzo
Lorenzo
Minghini
0000281742
[email protected]
0000286147
[email protected]
0000279040
[email protected]
Sommario
Questa relazione propone la valutazione indiretta dell’impedenza di carichi
resistivi. Per la legge di Ohm, sono necessari i valori istantanei di tensione
ai capi e corrente attraverso il carico; se la misura avviene contemporaneamente con due strumenti, però, l’amperometro falsa la misura del voltmetro o
viceversa, quale che sia lo schema di connessione scelto. La parte introduttiva
distingue gli schemi da utilizzare a seconda del tipo di carico valutare (con
voltmetro a valle o a monte). Successivamente, noti nominalmente o sperimentalmente i carichi, dopo aver effettuato le misure si verificano l’accuratezza
delle stime operate per via indiretta (cioè con la legge di Ohm) e l’efficacia
dei metodi impiegati.
Indice
2
Indice
Simbologia
2
1 Finalità e obiettivi
3
2 Metodo operativo
2.1 Materiale utilizzato . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Schemi di collegamento e dettagli operativi . . . . . . . . . . . . . .
2.3 Driver . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
3
4
6
3 Risultanze
6
4 Considerazioni finali
7
Elenco delle figure
9
Elenco delle tabelle
9
Riferimenti bibliografici
9
Simbologia
Vp
VV
Z
Significato
Parametro di correzione di ML , fornito dal costruttore
Tensione di alimentazione del carico
Corrente di carico
Corrente misurata dall’amperometro
Corrente attraversante il voltmetro
Misurando generico
Stima del misurando M attraverso processi di misurazione
Incertezza associata alla stima del misurando M
Incertezza di tipo A (letture ripetute) del misurando M
Incertezza combinata del misurando M
Valore del misurando M letto dallo strumento
Valore vero del misurando M
Potenza dissipata dal carico
Resistenza interna dell’amperometro
Resistenza interna del voltmetro
Tensione di carico
Tensione ai capi dell’amperometro
VF S
Portata scelta sullo strumento (anche
)
2
Tensione misurata dal voltmetro
Impedenza di carico
Tabella 1: Riepilogo della simbologia utilizzata
=
$
CC
BY:
\
Simbolo
c
E
I
IA
IV
M
M̂
u(M̂ )
uA (M̂ )
uc (M̂ )
ML
Mx
PZ
RA
RV
V
VA
1 Finalità e obiettivi
1
3
Finalità e obiettivi
Ciascun del proprio cuor l’altrui misura.
- Pietro Metastasio -
L’equazione che mette in relazione tensione e corrente in un bipolo (legge di
Ohm)
V = R·I
deve probabilmente buona parte della propria fortuna alla costanza di R nelle applicazioni in cui è utilizzata. La resistenza di un generico resistore o di una rete
resistiva ad esso riconducibile è, nominalmente, costante. In tali casi è sufficiente
misurare uno degli altri due parametri (usualmente V per semplicità, infatti per misurare I bisogna porsi a collegamento in serie e non sempre è possibile interrompere
un circuito; ad es. nei circuiti stampati) e, noto R, si ricava il terzo.
Il grande pregio della legge di Ohm è, però, la sua versatilità di interpretazione.
Se ne appena vista la definizione “corrente I attraverso una resistenza R con caduta
di tensione V ai capi”. Un’altra visione opposta è quella di “resistenza offerta a una
tensione V che provoca una corrente I”, che è poi l’uso più generico e probabilmente
il vero motivo per cui la legge è intitolata all’uomo col cui nome si misurano, oggi,
tutte le resistenze.
Il problema di misurare contemporaneamente tensione e corrente di un bipolo è
notevole per le complicazioni che si manifestano appena si passa dall’ipotesi ideale
di misura a quella reale. Nel caso nominale, la tensione è misurata da un voltmetro
con resistenza interna RV → ∞ e la corrente da un amperometro con RA = 0;
per questo, uno qualunque degli schemi in figura 1 o 3 andrebbe benissimo, perché
ogni strumento ideale non si farebbe misurare dall’altro. Nella realtà, in qualunque
schema, o il voltmetro misura la piccola tensione dell’amperometro, o l’amperometro
misura la piccola corrente del voltmetro; in tutti i casi, questa misura si sovrappone
a quella di tensione e corrente del carico, falsandola.
È bene precisare che lo schema perfetto non esiste. La soluzione consiste nel
trovare uno stratagemma che immunizzi il processo di misura dai condizionamenti
vicendevoli degli strumenti. Nel seguito sono descritti i due metodi di connessione
che limitano le influenze di misura e i limiti di operatività previsti per ciascuno.
Reperiti un carico di piccola entità e uno duecento volte maggiore, si sono poi
misurate le caratteristiche volt-amperometriche di ognuno col metodo più indicato.
Nelle conclusioni sono riportati i risultati ed è tracciata un’analisi sulla loro rispondenza rispetto ai dati reali a disposizione; in particolare, il confronto è interessante
per un carico resistivo (un resistore) misurato volt-amperometricamente e poi con
un ohmetro, per cui si hanno a disposizione due stime e si può valutare l’accuratezza
e la compatibilità delle misure.
2
Metodo operativo
2.1
Materiale utilizzato
Per ottenere le misure sono stati utilizzati i seguenti materiali, forniti dal laboratorio
di Elettronica e Telecomunicazioni della Facoltà:
• multimetri digitali (marca Agilent, mod. 34401A) (n. 2);
• breadboard;
• resistori da 150 Ω (n. 6) e da 22 kΩ (n. 1);
• PC (n. 2) con software LabVIEW e connessione al multimetro;
• cavi di collegamento.
\
=
$
CC
BY:
2.2 Schemi di collegamento e dettagli operativi
2.2
4
Schemi di collegamento e dettagli operativi
Operativamente è facile e conveniente distinguere i due metodi utilizzati nel corso
del test, identificandoli con la posizione del voltmetro rispetto all’amperometro: a
valle, oppure a monte.
Ia
I
E
V
Z
Iv
Vv
Figura 1: Circuito di misura con voltmetro a valle
Voltmetro a valle. Lo schema utilizzato per la misura con voltmetro a valle è
in figura 1. Questa configurazione è indicata per misure con corrente sul carico
elevata: a parità di tensione di alimentazione, il carico sarà quindi di piccolo valore.
Infatti è possibile scrivere:
VV = V
IA = IV + I errore di consumo del voltmetro
V
. In particolare diventerà IA ' I quando I è molto grande, e quindi
RV
IV si trascura.
Abbiamo identificato come carico di modesta entità un bipolo con resistenza
attorno ai 100 Ω il quale, alimentato a 10 V, vede una corrente attraverso di sé pari
a circa 100 mA. Tale valore non è tanto elevato quanto sperato, ma alcuni motivi
pratici hanno impedito di raggiungere la soglia dell’ampère che avrebbe reso più
probante il test. Come prima motivazione, si è voluto evitare il rischio di correnti
troppo elevate, che pregiudicassero l’incolumità degli operatori e degli strumenti;
come seconda causa si è posto un problema di dissipazione della potenza. I resistori
a disposizione hanno un valore massimo di potenza dissipabile pari a 250 mW; per
una relazione ben nota, la massima corrente che può scorrere attraverso un resistore
Z = 100 Ω è:
r
PZ
2
PZ = ZI ⇒ I =
= 50 mA
Z
cioè la metà di quella richiesta. Diminuendo ulteriormente Z, a parità di PZ ,
aumenta la corrente massima che si può far scorrere, ma contestualmente aumenta
anche la corrente effettiva che scorre per effetto della legge di Ohm nel circuito:
questa non è, dunque, una soluzione al problema.
Un metodo è proposto nello schema 2: i sei resistori, nominalmente uguali,
R
connessi in tal modo costituiscono un carico con resistenza Z = 2 · . È facile
3
verificare che, con R = 150 Ω, si ottiene il richiesto Z = 100 Ω. La corrente su
ogni resistore è un terzo di quella totale, cioè circa 33 mA; allora ogni resistore
dissipa circa PZ ' 100 Ω · (33 mA)2 ' 110 mW, cioè meno della metà della potenza
massima dissipabile per ogni resistore.
Poiché, in definitiva, la corrente raggiunge i 100 mA durante il test, assumiamo
come valida l’approssimazione di “I grande” considerati i mezzi a disposizione.
Riepilogando, i parametri della misurazione (anche cfr. [2, p. 216]) sono:
con IV =
alimentazione: E = 10 V;
carico: Z = 100 Ω;
\
=
$
CC
BY:
2.2 Schemi di collegamento e dettagli operativi
5
R
R
R
R
R
R
Figura 2: Carico misurato con voltmetro a valle (R = 150 Ω)
voltmetro: portata 10, 00 V (d1 = 0, 0035; d2 = 0, 0005);
amperometro: portata 100, 00 mA (d1 = 0, 050; d2 = 0, 005).
Ogni misurazione ha previsto il rilievo contemporaneo di tensione e corrente, ciascuna tramite dieci letture con cadenza 500 ms. In totale sono state effettuate due
misurazioni cosı̀ organizzate, con un intervallo tra le due di circa un minuto.
Va
Ia
Iv
E
Vv
I
V
Z
Figura 3: Circuito di misura con voltmetro a monte
Voltmetro a monte. Lo schema utilizzato per la misura con voltmetro a monte
è in figura 3. Questa configurazione è indicata per misure con corrente modesta
sul carico, perciò a parità di tensione di alimentazione il carico sarà grande. Infatti
valgono le relazioni:
IA = I
VV = VA + V errore di consumo dell’amperometro
con VA = RA I. In particolare diventerà VV ' V quando I è molto piccola, e quindi
VA si trascura.
Nella scelta del carico di notevole entità è stato riscontrato un problema, che
inizialmente pareva insormontabile. Scelto inizialmente un resistore da 1 MΩ e
procedendo alla misura con alimentazione a 10 V e fondoscala dell’amperometro
10 mA, questi leggeva valori di corrente di molto inferiori a quelli nominalmente
previsti (alcuni nanoampère invece di circa 10 µA), probabilmente perché la corrente
non era tale da essere apprezzabile. Considerata troppo elevata la resistenza, è
stata sostituita con una differente pari a 100 kΩ, ottenendo gli stessi problemi.
Proseguendo nella riduzione di un ordine di grandezza alla volta, la verifica con un
resistore disponibile da 22 kΩ è stata positiva ed il resistore è stato scelto per il
test. La corrente non supera, durante il test, i 500 µA, quindi con il materiale a
disposizione è legittimo considerare valida l’approssimazione di “I piccola”.
Riepilogando, i parametri della misurazione (anche cfr. [2, p. 216]) sono:
alimentazione: E = 10 V;
\
=
$
CC
BY:
2.3 Driver
6
carico: Z = 22 kΩ;
voltmetro: portata 10, 00 V (d1 = 0, 0035; d2 = 0, 0005);
amperometro: portata 10, 00 mA (d1 = 0, 050; d2 = 0, 020).
Ogni misurazione ha previsto il rilievo contemporaneo di tensione e corrente, ciascuna tramite dieci letture con cadenza 500 ms. In totale sono state effettuate due
misurazioni cosı̀ organizzate, con un intervallo tra le due di circa un minuto.
2.3
Driver
Per ottenere le stime dei misurandi e poterne calcolare le incertezze sono stati utilizzati i multimetri (uno come voltmetro, l’altro come amperometro) pilotati da
due copie identiche di un driver realizzato e compilato con il codice LabVIEW1 .
Ogni driver risiedeva su un diverso PC, cui era collegato il relativo multimetro:
per questo motivo, le misurazioni dei due strumenti non sono avvenute in perfetto sincrono, benché il comando di lettura da driver sia stato dato dall’operatore
contemporaneamente a entrambi gli strumenti.
3
Risultanze
Voltmetro a valle. In tabella 2 sono trascritte le stime rilevate nei due processi
di misurazione volt-amperometrici con voltmetro a valle rispetto all’amperometro.
M
VV(v1)
IA(v1)
VV(v2)
IA(v2)
[V]
[A]
[V]
[A]
M̂x
9,928891
0,1005594
9,929352
0,100561
u2A (M̂L )
2, 4923 · 10−11
1, 0441 · 10−12
5, 2184 · 10−11
7, 1383 · 10−13
u2A (ĉ)
5, 2672 · 10−8
1, 0186 · 10−9
5, 2676 · 10−8
1, 0187 · 10−9
u2c (M̂x )
5, 2697 · 10−8
1, 0197 · 10−9
5, 2728 · 10−8
1, 0194 · 10−9
Tabella 2: Misure volt-amperometriche con voltmetro a valle
Voltmetro a monte. In tabella 3 sono riportate le stime rilevate nei due processi
di misurazione volt-amperometrici con voltmetro a monte rispetto all’amperometro.
La tabella 4, invece, mostra la misura effettuata col multimetro in configurazione
ohmetro sul resistore utilizzato come carico, avente valore nominale 22 kΩ; questa
stima servirà come metro di paragone del risultato volt-amperometrico e per darne
una valutazione di efficacia.
M
VV(m1)
IA(m1)
VV(m2)
IA(m2)
[V]
[A]
[V]
[A]
M̂x
9,993429
4, 60889 · 10−4
9,993816
4, 60629 · 10−4
u2A (M̂L )
2, 1599 · 10−9
6, 1393 · 10−16
5, 8391 · 10−11
1, 1959 · 10−16
u2A (ĉ)
5, 3272 · 10−8
1, 6583 · 10−12
5, 3276 · 10−8
1, 6581 · 10−12
u2c (M̂x )
5, 5432 · 10−8
1, 6589 · 10−12
5, 3334 · 10−8
1, 6582 · 10−12
Tabella 3: Misure volt-amperometriche con voltmetro a monte
M
Z(m)
M̂x
[Ω]
21.668, 9
u2A (M̂L )
[Ω]
38, 6621 · 10−3
u2A (ĉ)
[Ω]
3, 3431
u2c (M̂x )
[Ω]
3,3817
uc (M̂x )
[Ω]
1,8
Tabella 4: Misura del resistore utilizzato come carico con voltmetro a monte
1 Ulteriori dettagli nella nostra relazione “Misura del parametro di attenuazione di una rete
resistiva partitrice di tensione” (31 ottobre 2008).
\
=
$
CC
BY:
4 Considerazioni finali
4
7
Considerazioni finali
Voltmetro a valle. I valori di impedenza Z del carico stimato con voltmetro a
valle, ottenuti rapportando nelle due distinte misurazioni la tensione e la corrente
misurate dagli strumenti, sono in tabella 5 assieme all’incertezza di misura e all’incertezza relativa. Si nota subito che le misure presentano medesima incertezza
e scostamento tra esse di soli 3 millesimi di ohm, quindi la misura è stata molto
accurata.
M
M̂
uc (M̂ )
Z(v1)
Z(v2)
[Ω]
98,737
98,740
[Ω]
0,031
0,031
uc (M̂ )
M̂
[%]
0,0318
0,0318
Tabella 5: Stime di Z con voltmetro a valle
Il risultato della misura è, dunque:
Z(v)nom = 100 Ω
;
Ẑ(v)V A = 98, 737(31) Ω
Appare evidente la differenza tra il valore nominale del carico (100 Ω) e quello stimato in 98, 737(31) Ω. Benché la differenza superi 1 Ω di valore ed ecceda l’incertezza,
questa non sorprende: la tolleranza nominale del 10% sulla resistenza dei resistori ne
comporta una grande dispersione del valore. In resistori da 100 Ω, ciò significa che
essi possono assumere un valore compreso tra 90 e 110 Ω; questa grande incertezza
si propaga, considerando lo schema connettivo utilizzato (figura 2) e le ulteriori
incertezze dovute alla connessione. Per questi motivi è plausibile che questo carico,
in generale, abbia un valore vero di resistenza lontano da 100 Ω nominali: non ha,
dunque, senso paragonare questo valore con la stima effettuata. Nel caso specifico
è, anzi, sorprendente che il valore vero sia cosı̀ simile a quello ideale.
Non avendo dati reali a disposizione per un confronto, ci limitiamo a osservare
che la misura è apparsa di buona qualità per questo piccolo carico, generando due
risultati molto prossimi anche a distanza di molti secondi e dando, perciò, un’impressione di stabilità complessiva del sistema non disprezzabile (interpretabile come
assenza di perturbazioni). Concludiamo confermando che la soluzione adottata sul
carico per ripartire la potenza è stata efficace: il carico stesso non produceva calore,
mentre la stabilità della misura conferma che non erano in atto fenomeni rilevanti
di rumore termico.
Voltmetro a monte. I valori di impedenza Z del carico stimato con voltmetro a
monte, ottenuti rapportando nelle due distinte misurazioni la tensione e la corrente
misurate dagli strumenti, sono in tabella 6 assieme all’incertezza di misura e all’incertezza relativa. Anche in questo caso si nota che le misure presentano la stessa
incertezza, mentre lo scostamento tra esse aumenta a 13 Ω: la misura è parimenti
accurata, però, se si considerano queste differenze in senso relativo.
M
M̂
uc (M̂ )
Z(m1)
Z(m2)
[Ω]
21.683
21.696
[Ω]
61
61
uc (M̂ )
M̂
[%]
0,279
0,280
Tabella 6: Stime di Z con voltmetro a monte
Il risultato della misura è, allora:
Z(m)nom = 22 kΩ
;
Ẑ(m)V A = 21, 683(61) kΩ
\
=
$
CC
BY:
4 Considerazioni finali
8
In entrambi i risultati la differenza dal valore nominale è significativa e penalizzante.
Nel caso in questione, però, si è potuto misurare il valore di resistenza del carico e
darne una stima (tab. 4), cosicché si considera il confronto:
Ẑ(m) = 21, 6689(18) kΩ
Ẑ(m)V A = 21, 683(61) kΩ
;
Si nota che la stima resistiva Ẑ(m) è dispersa all’interno dell’intervallo di dispersione
della stima volt-amperometrica:
Ẑ(m) ∈ [21, 6671 , 21, 6707]
⊂
Ẑ(m)V A ∈ [21, 622 , 21, 744]
La compatibilità tra le due misure, quindi, è forte. In maniera legittima, inoltre, la
stima resistiva è più precisa di quella indiretta volt-amperometrica, che risente di
un’incertezza maggiore dovuta in parte alla legge di propagazione dell’incertezza.
Notiamo che, se avessimo considerato come risultato definitivo della misura lo
scartato Z(m2) , avremmo ottenuto il medesimo riscontro di compatibilità. Questa
precisazione è confortante nell’affermare l’affidabilità e l’efficacia del processo di
misurazione cosı̀ organizzato, che ha restituito un risultato ogni volta compatibile
con la miglior stima rilevabile del carico (tramite ohmetro) e da esso differente per
meno dell’1, 5%.
\
=
$
CC
BY:
Elenco delle figure
9
Elenco delle figure
1
2
3
Circuito di misura con voltmetro a valle . . . . . . . . . . . . . . . .
Carico misurato con voltmetro a valle (R = 150 Ω) . . . . . . . . . .
Circuito di misura con voltmetro a monte . . . . . . . . . . . . . . .
4
5
5
Elenco delle tabelle
1
2
3
4
5
6
Riepilogo della simbologia utilizzata . . . . . . . . . . .
Misure volt-amperometriche con voltmetro a valle . . . .
Misure volt-amperometriche con voltmetro a monte . . .
Misura del resistore utilizzato come carico con voltmetro
Stime di Z con voltmetro a valle . . . . . . . . . . . . .
Stime di Z con voltmetro a monte . . . . . . . . . . . .
.
.
.
a
.
.
. . . .
. . . .
. . . .
monte
. . . .
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
2
6
6
6
7
7
Riferimenti bibliografici
[1] Agilent. Agilent 34401A - Guida d’uso, 3rd edition, March 2003.
[2] Agilent. Agilent 34401A - User’s guide, 7th edition, August 2007.
\
=
$
CC
BY:
Quest’opera è stata rilasciata sotto la licenza Creative Commons Attribuzione-Non commerciale-Non opere derivate 2.5 Italia. Per leggere
una copia della licenza visita il sito web
http://creativecommons.org/licenses/by-nc-nd/2.5/it/
o spedisci una lettera a Creative Commons, 171 Second Street, Suite
300, San Francisco, California, 94105, USA.
È consentito riprodurre e distribuire liberamente il presente testo, senza apporvi modifiche e mantenendo sempre riconoscibile il nome degli autori, purché non
a scopo di lucro, senza scopi commerciali (direttamente o indirettamente) e per
esclusivo uso personale.
È possibile pubblicare il file o sue parti su siti internet, purché siano citati in
maniera evidente gli autori (Marco Alessandrini, Alessandro Callozzo e Lorenzo
Minghini).
Per qualunque informazione, problematica, suggerimento o reclamo utilizzare
l’indirizzo [email protected].
\
=
$
CC
BY: