leggi

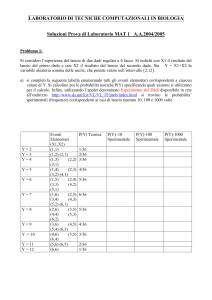
Introduzione ai fenomeni casuali: frequenza relativa, probabilità matematica, legge dei grandi numeri
di Luciano Porta
I principi che regolano i fenomeni casuali o aleatori sono talvolta controintuitivi. Pertanto ritengo sia
didatticamente indispensabile studiare questi fenomeni prima dal punto di vista frequentista e poi da
quello probabilistico (con l’aiuto iniziale di schemi grafici). Infine la legge dei grandi numeri, formulata in
modo semplificato, darà sistemazione teorica all’accordo che gli studenti hanno già verificato tra i risultati
delle loro esperienze e i valori attesi (insisto in questo preciso ordine).
Iniziamo con la definizione di fenomeno casuale (dalla parola caso) o aleatorio (dalla parola alea = dado) :
è casuale un fenomeno che non possiamo prevedere se si verificherà o no (ad esempio lanciando una
moneta non sappiamo se uscirà testa o croce; gettando un dado non sappiamo quale faccia uscirà ...).
I primi studi di Pacioli, Cardano, Galilei, Pascal, Fermat furono sollecitati da quesiti posti dal gioco d’azzardo
(ad esempio come doveva essere suddivisa la posta in gioco se la partita era stata interrotta). Studi più
rigorosi e generali nel campo degli eventi aleatori furono effettuati dal matematico svizzero Jakob Bernoulli
(1654 – 1705) che formulò al legge dei grandi numeri. La definizione classica di probabilità, che noi
adotteremo, è stata introdotta dal matematico francese Pierre Simon De Laplace (1749 – 1827).
Successivamente sono state date altre definizioni di probabilità ( Kolmogorov, De Finetti).
Attualmente non vi è scienza che non si serva di questo ramo della matematica (ad esempio la genetica per
studiare la trasmissione dei caratteri ereditari).
Possiamo studiare gli eventi casuali o con il concetto di frequenza relativa (F.R.) sperimentalmente o con il
concetto di probabilità matematica (P.M.) teoricamente. La legge dei grandi numeri collega questi due
concetti tra di loro.
Frequenza relativa (si calcola dopo aver eseguito molte volte l’esperienza)
La frequenza relativa del verificarsi di un evento è il rapporto tra il numero di volte che l’evento si è
manifestato e il numero totale di eventi.
F.R. = n. volte evento considerato / n. totale eventi
La classe sarà divisa in gruppi, ciascuno dei quali eseguirà una certa esperienza, raccoglierà ed elaborerà i
dati e li comunicherà alla classe intera. E’opportuno che molti dei casi oggetto in seguito del calcolo della
probabilità matematica, siano prima affrontati sperimentalmente e di essi sia calcolata la frequenza
relativa.
Nel caso di esperienze da ripetere moltissime volte per ottenere risultati significativi (come il lancio di una
coppia di dadi per poi calcolare la somma delle facce uscite) possiamo ricorrere ad una simulazione al
computer.
Esempi di determinazione della frequenza relativa (i dati sono stati ottenuti da esperienze reali).
Si è lanciata 200 volte una moneta e 94 volte è uscita testa e 106 volte croce. Determiniamo la frequenza
relativa:
F.R. (testa) = 94/200 = 0,47 = 47 %
F.R. (croce) =106/200 = 0,53 = 53 %
Osserviamo che F.R. (testa) + F.R. (croce) = 1 = 100 %
E’ gettato 300 volte un dado e ogni volta si annota la faccia uscita ottenendo 46 volte la faccia 1, 55 quella
2, 52 quella 3, 48 quella 4, 45 quella 5 e 54 quella 6. Determiniamo la frequenza relativa di ogni faccia.
F.R.(1) = 46/300 = 0,15(3) = 15,(3)% F.R.(2) = 55/300 = 0,18(3) = 18,(3)% F.R.(3) = 52/300 = 0,17(3) = 17,(3)%
F.R.(4) = 48/300 = 0,16 = 16%
F.R.(5) = 45/300 = 0,15 = 15%
F.R.(6) = 54/300 = 0,18
= 18%
1
Osserviamo che addizionando tutte le frazioni si ottiene come somma 300/300 = 1 (100 %).
Determiniamo ora, dalla stessa esperienza, altre frequenze relative.
F.R. (pari) = (55 + 48 + 54)/300 = 157/300 = 0,52(3)
F.R. (dispari) = 1 – 157/300 = 143/300 = 0,47(6)
F.R. (numero > 4) = (45 + 54)/300 = 99/300 =0,33
F.R. (n. < 5) = 1 – 99/300 = 201/300 = 0,67
Si estrae da un mazzo di 40 carte francesi una carta e si annota se è una figura o una non figura, la si
rimette nel mazzo, si rimescola con cura e si ripete complessivamente la procedura 200 volte.
Si estrae 56 volte figura e 144 non figura. Determiniamo le frequenze relative:
F.R. (figura) = 56/200 = 0,28 = 28 %
F.R. (non figura) = 144/200 = 0,72 = 72/%
Osserviamo che F.R. (figura) + F.R. (non figura) = 1 = 100 %
E’ lanciata 400 volte una coppia di monete ottenendo 48 volte T-T, 52 volte T-C, 46 volte C-T e 54 volte C-C.
Determiniamo le frequenze relative:
F.R. (T-T) = 0,24 = 24 % F.R. (T-C) = 0,26 = 26 % F.R. (C-T) = 0,23 = 23% F.R. (C-C) = 0,27 = 27 %
Osserviamo che F.R. (T-T) + F.R. (T-C) + F.R. (C-T) + F.R. (C-C) = 1 = 100 %
Simuliamo al computer il lancio di un coppia di dati (400 volte) e sommiamo ogni volta le facce uscite.
L’ immagine è la schermata di un mio semplice programma (didascalia : FR A frequenza assoluta; FR R
frequenza relativa; PM probabilità matematica):
Finiamo osservando che: 0 <= F.R. <= 1 (0 se l’evento non si è mai verificato e 1 se si è sempre verificato).
Probabilità matematica (definizione classica di Laplace)
La probabilità matematica è il rapporto tra il numero dei casi favorevoli (all’evento) e il numero dei casi
possibili, purché tutti ugualmente possibili.
P.M. = n.casi favorevoli / n.casi possibili
Esempi di determinazione della probabilità matematica:
Determinare la P.M. di ottenere testa lanciando una moneta. Ugualmente la P.M. di ottenere croce.
P.M. (testa) = C.F./C.P. = ½ = 0,5 = 50% P.M. (croce) = ½ = 0.5 = 50% P.M. (testa) + P.M. (croce) = 1 = 100%
2
Determinare la P.M. di ottenere la faccia 5 gettando un dado. Determinare la P.M. di ottenere numero pari.
Determinare la P.M. di ottenere numero >4.
P.M. (5) = 1/6 = 0,1(6)
P.M. (pari) = 3/6 = 0,5 = 50%
P.M. (numero > 4) = 2/6 = 0,(3)
Determinare la P.M. di estrarre da un mazzo di 40 carte francesi figura. Determinare la P.M. di non figura.
P.M. (figura) = 12/40 = 0,3 = 30% P.M. (non figura) = 28/40 = 0,7 = 70% P.M. (figura) + P.M. (non figura) = 1
In un’urna vi sono 25 palline gialle e 15 verdi. Determinare la P.M. di estrarre pallina gialla. Determinare
ugualmente la P.M. di estrarre pallina verde.
P.M. (gialla) = 25/(25 +15) = 25/40 = 0,625 = 62,5%
P.M. (verde) = 15/(25 + 15) = 0,375 = 37,5%
Terminiamo osservando che: 0 <= P.M. <= 1 (0 se l’evento è impossibile, come l’estrarre pallina nera da
un’urna contenente solo palline bianche e 1 se è certo, come estrarre pallina gialla da un’urna contenente
solo palline gialle; l’evento è incerto negli altri casi).
Affrontiamo ora altri esempi di maggiore complessità nel calcolo della P.M.
In un’urna vi sono 15 palline nere, 5 bianche e 20 rosse.
Determinare la P.M. di estrarre pallina nera, la P.M. di estrarre pallina bianca, la P.M. di estrarre pallina
nera o bianca (riflettiamo sul significato di o: è indifferente N o B), la P.M. di estrarre pallina nera o rossa.
P.M. (nera)=15/(15+5+20)=15/40=0,375=37,5% P.M. (bianca)=5/40=0,125=12,5%
P.M. (nera o bianca)=(15+5)/40=20/40=0,5=50% P.M. (nera o rossa)=(15+20)/40=35/40=0,875 = 87,5%
Determinare la P.M. di estrarre da un mazzo di 40 carte francesi una figura, la P.M. di estrarre non figura, la
P.M. di estrarre figura o carta di cuori (dobbiamo contare una volta sola le figure di cuori).
P.M. (figura) = 12/40 = 0,3 = 30%
P.M. (non figura) = 28/40 = 0,7 = 70%
P.M. (figura o cuori) = (12 + 7)/40 = 19/40 = 0,475 = 47,5% o anche: (9 + 10)/40 = 19/40 ...
Avendo 2 dadi, gettandoli insieme, determinare la P.M. di ottenere la somma 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Tracciamo una tabella a doppia entrata (ponendo ad es. sul lato verticale le facce del primo dado e sul lato
orizzontale le facce del secondo dado, la somma sarà nella casella incrocio tra riga e colonna).
3
Osserviamo che 7 è la somma più probabile perche si può ottenere in più modi, rispetto alle altre.
Determinare la P.M. di ottenere lanciando due monete: T-T, T-C, C-T, C- C.
Per determinare il numero di casi favorevoli e di casi possibili possiamo ricorrere o ad una tabelle a doppia
entrata o ad un diagramma ad albero.
Anche i genetisti utilizzano una tabella a doppia entrata, denominata scacchiera o quadrato di Punnet, per
determinare la probabilità che un individuo, derivante da un incrocio, presenti certi caratteri.
Ad esempio ricordando che nella Mirabilis ialapa (bella di notte) non esiste dominanza per il colore del
fiore, incrociando due individui eterozigoti rosa (RB), determiniamo la P.M. di ottenere individui omozigoti
rossi (RR), individui omozigoti bianchi (BB) e individui eterozigoti rosa (RB o BR).
Determinare la P.M. che i tre figli di una coppia siano femmine. Usiamo solamente il diagramma ad albero.
4
In un’urna sono contenute quattro palline (1 bianca, 1 nera, 1 verde e 1 rossa).
a) Determinare la P.M. di estrarre nell’ordine pallina bianca e pallina nera (riflettere sul significato di e),
rimettendo nuovamente nell’urna la pallina prima estratta.
b) Determinare la P.M. di estrarre nell’ordine pallina bianca e pallina nera (riflettere sul significato di e),
senza rimettere nell’urna la pallina prima estratta (in questo caso si considera estratta la pallina bianca che
non viene reintrodotta nell’urna).
Legge dei grandi numeri (di Jakob Bernoulli) (enunciato semplificato per fini didattici)
Maggiore è il numero delle prove, più la frequenza relativa si approssima alla probabilità matematica.
Come abbiamo verificato sperimentalmente quando il numero delle prove è molto elevato, la F.R. si
avvicina molto alla P.M. Possiamo così usare indifferentemente o la F.R. o la P.M. Vi sono delle situazioni
problematiche in cui è preferibile la determinazione della P.M. (evitiamo l’esecuzione di esperienze in
numero molto elevato) e situazioni in cui l’interpretazione frequentista è indispensabile (ad esempio per
determinare per scopi assicurativi l’aspettativa di vita di una persona che oggi compie 70 anni dobbiamo
ricorrere ad indagini statistiche).
Sulla legge dei grandi numeri si basa anche il metodo Montecarlo. Dobbiamo ad esempio determinare il
valore approssimato di π con questo metodo (vedi apposita lezione per una trattazione più completa).
Osserviamo che il rapporto K tra area del cerchio e area del quadrato circoscritto è π/4 da cui π=4K.
Possiamo determinare approssimativamente il valore di K simulando la seguente situazione: un poligono di
tiro ha la forma di un cerchio inscritto in un quadrato. Al centro del cerchio c’è un cannone che spara con
direzione e gittata casuale: il rapporto K tra l’area del cerchio e quella del quadrato, se gli spari sono molto
numerosi, è uguale al rapporto tra il numero dei proiettili che cadono nel cerchio e il numero dei proiettili
che cadono nel quadrato (cerchio compreso). La situazione può essere ulteriormente semplificata
pensando ad un cannone che spara in un poligono come quello rappresentato nell’immagine.
5
La posizione del punto in cui il proiettile cade sul poligono di tiro è determinata da due numeri pseudo
casuali (compresi tra 0 e 1), l’ascissa e l’ordinata. Applicando il teorema di Pitagora calcoliamo se il punto
cade nel cerchio (ipotenusa <= 1) o nel quadrato, cerchio compreso, (ipotenusa >1). La radice quadrata è
superflua.
Di seguito è trascritto un mio semplice programma in linguaggio BBC Basic (2008) per determinare π col
metodo Montecarlo con la schermata ottenuta dopo averlo fatto girare.
Errori più frequenti nel concetto di probabilità
Derivano soprattutto dalla non comprensione della legge dei grandi numeri.
1) Una persona lancia una moneta (non truccata) 5 volte ed esce sempre testa.
Alcuni pensano che il prossimo lancio sia aumentata la P.M. di uscita di croce. Altri confidano ancora
sull’uscita di testa. Sono entrambe convinzioni erronee perché la moneta non ha memoria e ogni lancio è
come se fosse il primo.
2) Una persona getta 15 volte un dado e non esce mai la faccia 2.
Alcuni pensano che il prossimo lancio sia aumentata la P.M. di uscita del 2, altri pensano che non uscirà il 2
neppure questa volta. Sono entrambe convinzioni erronee perché il dado non ha memoria e ogni lancio è
come se fosse il primo.
3) Una persona gioca inutilmente al lotto il n. 89 (ricordiamo che i numeri del lotto sono 90) sulla ruota di
Torino da 25 settimane.
Gioca anche la settimana seguente pensando che sia aumentata la P.M. della sua uscita.
La sua convinzione è errata poiché i numeri del lotto non hanno memoria e ogni estrazione è come se fosse
la prima. Con la stessa convinzione gioca anche le settimane seguenti aumentando ogni volta la somma
spesa sperando di ripianare le perdite, ma continua a perdere sempre di più, perché i numeri del lotto non
hanno memoria.
Non esistono metodi matematici per vincere, o per aumentare la probabilità di vincita, al gioco del lotto.
“In gran parte le questioni più importanti della vita sono di fatto solo problemi di calcolo della probabilità”
Pierre Simon de Laplace
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI DUE
6