Le altezze in prospettiva
I segmenti perpendicolari al PG e quindi le altezze di solidi, edifici, ecc., rimangono tali in prospettiva.
Le lunghezze di tali segmenti dipendono dalla distanza che essi hanno rispetto all’osservatore.
Illustriamo ora il procedimento che si utilizza per realizzare la prospettiva di un segmento AB perpendicolare
al PG.
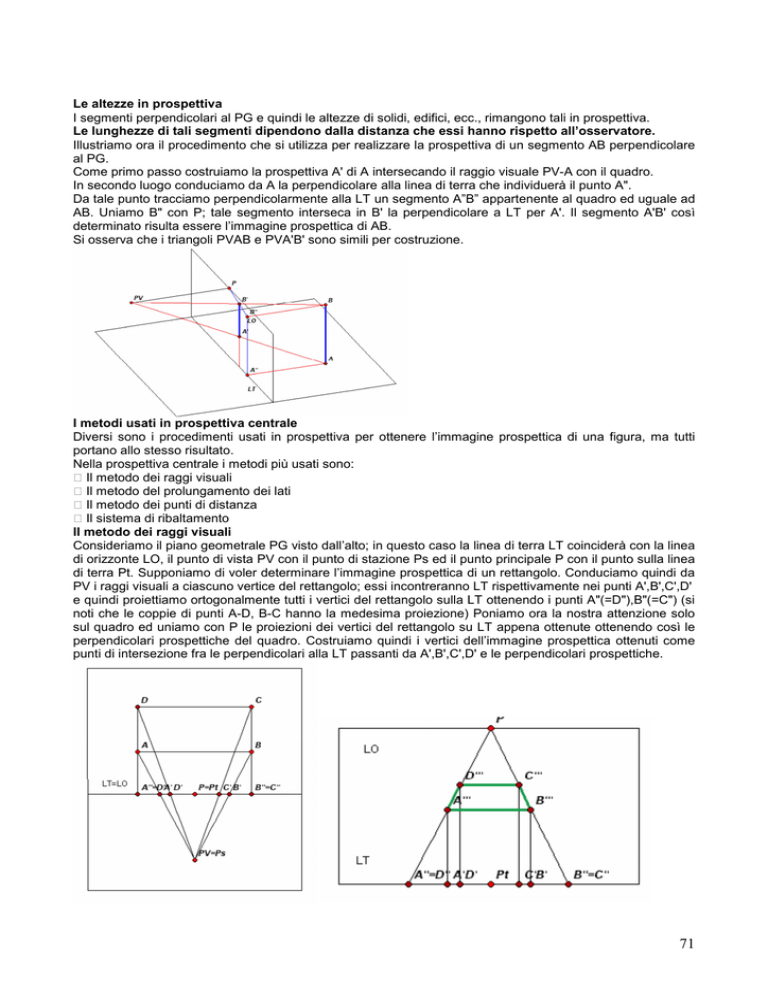
Come primo passo costruiamo la prospettiva A' di A intersecando il raggio visuale PV-A con il quadro.
In secondo luogo conduciamo da A la perpendicolare alla linea di terra che individuerà il punto A".
Da tale punto tracciamo perpendicolarmente alla LT un segmento A”B” appartenente al quadro ed uguale ad
AB. Uniamo B" con P; tale segmento interseca in B' la perpendicolare a LT per A'. Il segmento A'B' così
determinato risulta essere l’immagine prospettica di AB.
Si osserva che i triangoli PVAB e PVA'B' sono simili per costruzione.
I metodi usati in prospettiva centrale
Diversi sono i procedimenti usati in prospettiva per ottenere l’immagine prospettica di una figura, ma tutti
portano allo stesso risultato.
Nella prospettiva centrale i metodi più usati sono:
Il metodo dei raggi visuali
Il metodo del prolungamento dei lati
Il metodo dei punti di distanza
Il sistema di ribaltamento
Il metodo dei raggi visuali
Consideriamo il piano geometrale PG visto dall’alto; in questo caso la linea di terra LT coinciderà con la linea
di orizzonte LO, il punto di vista PV con il punto di stazione Ps ed il punto principale P con il punto sulla linea
di terra Pt. Supponiamo di voler determinare l’immagine prospettica di un rettangolo. Conduciamo quindi da
PV i raggi visuali a ciascuno vertice del rettangolo; essi incontreranno LT rispettivamente nei punti A',B',C',D'
e quindi proiettiamo ortogonalmente tutti i vertici del rettangolo sulla LT ottenendo i punti A"(=D"),B"(=C") (si
noti che le coppie di punti A-D, B-C hanno la medesima proiezione) Poniamo ora la nostra attenzione solo
sul quadro ed uniamo con P le proiezioni dei vertici del rettangolo su LT appena ottenute ottenendo così le
perpendicolari prospettiche del quadro. Costruiamo quindi i vertici dell’immagine prospettica ottenuti come
punti di intersezione fra le perpendicolari alla LT passanti da A',B',C',D' e le perpendicolari prospettiche.
71
Immagine prospettica di un esagono regolare.
Tracciamo dal PV i raggi visuali a ciascun vertice dell'esagono e chiamiamo A', B', C', D', E', F' le loro
intersezioni con la LT (punti rossi). Proiettiamo ortogonalmente tutti i vertici dell'esagono sulla LT ottenendo i
punti F", A2(=E"), B"(=D"), C" (punti verdi) . Sul quadro determiniamo i vertici dell'esagono intersecando le
perpendicolari alla LT passanti da A', B', C', D', E', F' con le perpendicolari prospettiche ottenute unendo P a
F", A", B", C" rispettivamente.
Il metodo del prolungamento dei lati
Come nel caso precedente consideriamo dapprima una visione dall’alto del piano geometrale.
Vediamo, mediante tale procedimento, come fare per determinare l’immagine prospettica di un esagono.
Una volta disegnato l’esagono prolunghiamo i lati EF e DC fino a determinare le rispettive tracce 1,2 sulla
LT. Tracciando quindi da PV le parallele ai lati ne determiniamo i punti di fuga in Fs e Fd. Nel caso
dell’esagono regolare in figura, in Fs concorrono i lati FA, DC e la diagonale EB; mentre in Fd i lati CB, EF e
la diagonale DA. Concentriamoci ora esclusivamente sul quadro e riportiamo su LO i punti P, Fs, Fd.
Tracciando dai punti 1, 2, A, B le rette concorrenti ai rispettivi punti di fuga è possibile determinare tutti gli
spigoli dell’esagono. Nella figura sottostante si è ampliato il procedimento al fine di ottenere la prospettiva di
una pavimentazione a maglia esagonale. Per ottenere ciò è sufficiente continuare a riportare sulla LT la
misura del lato dell’esagono per l’estensione voluta. È possibile completare il disegno in figura senza
determinare ulteriori tracce sulla LT ma unicamente completando il prolungamento dei lati all’infinito.
Il metodo dei punti di distanza
Questo metodo è basato sulla determinazione del cerchio di distanza come luogo geometrico dei punti di
fuga delle rette inclinate di 45° rispetto al quadro. Infatti per individuare il punto di fuga di una retta basta
portare da PV una parallela alla retta stessa: se questa è una retta a 45° il suo punto di fuga D disterà dal
punto principale P di una misura uguale a PV-P. Viceversa, disegnare sul quadro il cerchio di raggio PD
72
significa determinare il cerchio di distanza e quindi i punti di fuga di tutte le rette a 45°. Consideriamo quindi
la nostra solita visione dall’alto dove l’oggetto da rappresentare in prospettiva è un quadrato e tracciamo da
PV le rette inclinate di 45° rispetto alla LO determinando i punti di distanza D e D’. Per ciascun vertice del
quadrato conduciamo le parallele ad una di queste rette (ad esempio la retta per D') e quindi proiettiamo A,
B, C, E su LT ottenendo i punti A’(=E’) e B(=C’). Consideriamo ora soltanto il quadro e riportiamo sulla LT i
punti 1, 2, 3 e A', B' mentre sulla LO i punti D, P, D'. Congiungiamo 1, 2, 3 rispettivamente con D' e A', B' con
P. Le intersezioni di queste ultime con forniscono i vertici del quadrato in prospettiva cercato. Osserviamo
infine che avremmo ottenuto la stessa figura prospettica se avessimo ripetuto lo stesso procedimento
considerando le parallele alla retta per D.
Il sistema del ribaltamento
Tutti i metodi visti finora presentano, sostanzialmente, una grossa scomodità dovuta al fatto che, anche per
determinare l’immagine prospettica di un oggetto molto semplice quale ad esempio un quadrato, bisogna
ricorrere alla suddivisione del lavoro in due parti: la figura preparatoria sul PP e, in secondo luogo, la
costruzione della figura prospettiva sul quadro. Con il sistema di ribaltamento, per preparare l’esecuzione in
prospettiva occorre ribaltare di 90° sia il semipiano su cui giace la figura, sia il semipiano su cui sta il punto
di vista in modo che entrambi si trovino sullo stesso semipiano. In altre parole, con tale procedimento, si
riportano l’oggetto iniziale ed il PV sul medesimo semipiano in modo tale che quest’ultimo si possa
considerare come il prolungamento del quadro sotto la LT. Nella fase esecutiva si proiettano sulla LT i punti
significativi della figura che, in un secondo tempo, vengono uniti ai relativi punti di fuga mediante le rette
proiettanti. L’intersezione delle linee proiettanti forniscono i punti che uniti fra loro determinano l’immagine
prospettica dell’oggetto. Osserviamo che l’oggetto da rappresentare, considerato nel semipiano sottostante
al quadro, risulta rovesciato in pianta rispetto alla relativa immagine prospettica e che tali risulteranno essere
anche le rette necessarie per determinare i punti di fuga. Riassumendo, tre sono le caratteristiche di tale
procedimento:
ci consente di vedere in modo istantaneo il variare dell’immagine prospettica al mutare delle dimensioni
dell’oggetto considerato.
Possiamo vedere su un unico piano l’oggetto iniziale e la sua immagine prospettica (e quindi non abbiamo
più la necessità di suddividere il lavoro)
Permette una notevole rapidità esecutiva.
Quest’ultimo metodo appena descritto appare pertanto come il più semplice ed allo stesso tempo il
più completo nella determinazione delle immagini prospettiche.
73
La prospettiva accidentale
La prospettiva accidentale si differenzia da quella centrale per la diversa disposizione del quadro
prospettico. Questo, in genere, non è parallelo ai lati dell’oggetto da rappresentare rispetto ai quali assume
inclinazioni varie. Ciò dipende dagli effetti prospettici a cui si vuole giungere. Una buona prospettiva si
ottiene disponendo il quadro nella figura preparatoria con inclinazioni diverse, per esempio 30°, 60° rispetto
ai lati del rettangolo entro il quale è inquadrato l’oggetto, qualora lo stesso non presenti tali caratteristiche.
L’angolo minore è bene riferirlo al lato più importante della costruzione. La scelta del punto di vista ha una
parte predominante per la buona riuscita del disegno prospettico: la posizione è arbitraria ma è consigliabile
porlo ad una distanza tale che l’angolo formato tra i raggi visuali r ed r', che dal PV vengono diretti verso gli
estremi della figura rappresentata in pianta, sia contenuto attorno ai valori di 45°. In questo modo ci
assicuriamo che i raggi visuali stiano all'interno del cono ottico e quindi che l'immagine risultante sia
percettivamente corretta evitando così il fenomeno dell'aberrazione ottica.
L’ampiezza di tale angolo dipende sempre dalle dimensioni dell’oggetto da rappresentare in prospettiva.
Inoltre è bene che il prolungamento della proiezione del PV sul quadro cada all’interno della pianta.
I metodi usati in prospettiva accidentale
Come la prospettiva centrale, anche la prospettiva accidentale ha i suoi procedimenti per determinare
l’immagine prospettica dell’oggetto considerato. Essi sono:
Il metodo dei raggi visuali
Il metodo dei punti di distanza
Il metodo dei punti di fuga e delle perpendicolari al quadro
Il metodo dei punti misuratori
Osserviamo che i primi due metodi si utilizzano anche nella prospettiva centrale.
Il metodo dei raggi visuali
Consideriamo dapprima il piano geometrale visto dall’alto e riportiamo la linea di terra LT (coincidente con
LO), il punto di vista PV e la sua proiezione su LT Pt (coincidente con P). Supponiamo di voler determinare
l’immagine prospettica di un rettangolo ABCD. Seguendo le ormai note operazioni preparatorie, si
conducono dal PV le parallele ai lati del rettangolo di cui sopra che determinano i punti di fuga Fs ed Fd.
In essi concorrono rispettivamente tutte le rette parallele alle semirette che li hanno determinati. Dal PV si
conducono i raggi visuali verso i punti della pianta che intersecano la LT nei punti 1, 2, 3, 4 (si osservi che il
punto 3 è coincidente con A). Per la costruzione della prospettiva consideriamo il solo quadro e tracciamo su
di esso la LT e la LO alla distanza che crediamo più opportuna. Sulla LO riportiamo, nel rapporto stabilito, i
punti di fuga e sulla LT i punti 1, 2, 3, 4. Successivamente da 3 conduciamo le concorrenti a Fs e Fd che,
intersecate dalle verticali condotte dai punti 1 e 4 riportati sulla LT, forniscono i punti D' e B'.
Poiché rette parallele hanno il medesimo punto di fuga, tracciamo da B' la retta per Fs e da D' la retta per Fd.
Queste ultime due rette si incontreranno nel punto C' che dovrà coincidere con la perpendicolare a LT
tracciata dal punto 2.
74
Il metodo dei punti di distanza
Anche questo metodo ricalca fedelmente la costruzione fatta nel paragrafo precedente. Consideriamo
sempre il nostro piano geometrale visto dall’alto e costruiamo la prospettiva di un quadrato avente uno dei
vertici appartenente alla LT. Una volta scelto il PV, tracciamo sulla LT (coincidente con la LO) il punto Pt e i
punti di distanza D e D'. Quindi dai vertici del nostro quadrato conduciamo le parallele alla retta passante per
PV e D che intersecheranno la LT nei punti 1, 2, 3 rispettivamente. Tracciamo poi le proiezioni dei vertici B,
C, E sulla LT ottenendo i punti B', C' (coincidente con 1), E'. Abbiamo così ottenuto tutti gli elementi
essenziali per determinare la nostra immagine prospettica. Poniamo ora la nostra attenzione esclusivamente
sul quadro. Riportiamo la LO con i punti P, D, D' e la LT su cui tracciamo i punti appena determinati. Uniamo
le proiezioni dei vertici con il punto principale P e congiungiamo i punti 1, 2, 3 con D. Abbiamo così trovato i
vertici B", C", E" dell’immagine prospettica cercata.
Il metodo dei punti di fuga e delle perpendicolari al quadro
Questo metodo si basa sul principio dell’individuazione di qualsiasi spigolo dell’oggetto attraverso la ricerca
del punto di fuga della retta passante per esso. Determiniamo la prospettiva di un quadrato iniziando a
determinare i punti necessari alla costruzione sulla pianta. Consideriamo la visione dall’alto del nostro piano
geometrale. Come primo passo determiniamo i punti di fuga Fd, Fs dei lati del quadrato tracciando dal PV
rette parellele ad essi. Quindi prolunghiamo i lati del quadrato in modo da ottenere i punti 1, 2 come
intersezione di questi ultimi con la LT. Consideriamo ora solo il quadro e riportiamo i punti trovati sulla LT.
Uniamo A' (prospettiva di A) con Fs e Fd ottenendo così la prospettiva dei lati AE ed AB rispettivamente. In
modo analogo congiungiamo il punto 2 con Fs ed il punto 1 con Fd ottenendo così la prospettiva dei lati BC
ed EC rispettivamente. Per ultimare la figura basterà segnare le intersezioni di queste ultime rette che
forniranno i vertici A', B', C', E' del quadrato prospettico. Osserviamo che, qualora uno dei due punti 1 e 2
fosse risultato in pianta troppo lontano dal punto Pt, avremmo potuto trovare ugualmente la prospettiva della
figura ricorrendo almeno ad altri due procedimenti. Il primo ricorre al metodo delle rette perpendicolari al
quadro, il secondo si avvale dell'aiuto della geometria proiettiva. Applichiamo entrambi al nostro esempio.
75
Metodo delle rette perpendicolari al quadro
Supponiamo che il prolungamento del lato CB cada sulla LT troppo lontano e che quindi il punto 2 esca dal
nostro piano di lavoro. Per ovviare il problema consideriamo il vertice di tale lato che si trova più vicino alla
LT (B) e proiettiamolo ortogonalmente su di essa. Otteniamo un nuovo punto 2'. Per la costruzione della
figura si procede esattamente come in precedenza: uniamo i punti 1 ed A' con Fd e 2' con P. L’intersezione
fra le rette A'Fd e 2'P fornisce il vertice B' del quadrato che una volta unito con Fs darà luogo al vertice C'.
Ricerca dell'asse di collineazione
Come è possibile congiungere un punto P con l’intersezione di due rette che si intersecano fuori del foglio di
lavoro? La geometria proiettiva, di cui non parliamo, serve a rispondere al problema. Tracciamo per P due
segmenti che intersecano r ed r' in A e B e in A' e B' rispettivamente, in modo tale che le due rette AA' e BB'
si intersechino nel foglio, in un punto O. Ora tracciamo un'ulteriore retta per O, che intersecherà r e r' in C e
C' rispettivamente. Intersechiamo i segmenti BC' e B'C, otterremo un punto Q. La retta PQ passa per il punto
comune alle due rette (si chiama asse di collineazione della prospettività di centro O tra le due rette). Ecco
l’immagine che illustra la costruzione della figura del cubo, se dobbiamo congiungere un punto D con il punto
2 fuori dal foglio.
76
Il metodo dei punti misuratori
Tutti i metodi finora descritti presentano una certa difficoltà nella riproduzione delle dimensioni reali
dell’oggetto nell’immagine prospettica, infatti, le misure degli spigoli sono sempre proiettate sulla LT con
rapporti di riduzione od ingrandimento e mai nelle loro dimensioni effettive. Il metodo dei punti misuratori,
che deriva direttamente da quello dei punti di fuga, supera queste difficoltà basandosi sui principi contenuti
nel teorema di Talete sui segmenti proporzionali: rette parallele che intersecano due qualsiasi rette
appartenenti allo stesso piano determinano, su queste ultime, segmenti proporzionali.
Ne segue che le dimensioni dell’oggetto vengono riportate fedelmente od in modo proporzionale sulla LT.
Costruiamo quindi la figura preparatoria considerando la visione dall’alto del geometrale. Una volta scelto il
PV determiniamo sulla LT i punti di fuga Fs e Fd relativi ai lati AD (CB) e AB (DC) rispettivamente. Centriamo
quindi in Fs ed Fd e ribaltiamo il PV sulla LT dando luogo ai punti Ms ed Md rispettivamente.
Successivamente centriamo in A e ribaltiamo i punti B e D sulla LT dando origine ai punti B’ e D’. Poiché il
segmento che congiunge B con B’ risulta parallelo al segmento che congiunge il PV con Md, quest’ultimo
sarà il suo punto di concorso o misuratore. Lo stesso vale per Ms che risulta essere il punto misuratore del
segmento DD’ (parallelo al segmento PVMs) Passando all’immagine prospettica, posizionati gli usuali
elementi della prospettiva LO, LT, P, ed i punti di fuga Fs ed Fd riportiamo sull’orizzonte anche i punti
misuratori Ms ed Md. I punti misuratori sono punti di fuga che esercitano la loro influenza nelle porzioni di
spazio in cui si sono eseguiti i ribaltamenti, per cui nel disegno prospettico, una volta determinate le linee
principali della prospettiva (ovvero le rette AFs ed AFd) dobbiamo percorrere, dalle tracce sulla LT, le
porzioni di spazio comprese fra la LT e le linee principali della prospettiva concorrendo ai propri misuratori
situati dal lato opposto; nella restante porzione di spazio, compresa fra le AFs ed AFd, le rette
concorreranno normalmente ai rispettivi punti di fuga.
Proiezioni quotate
Le proiezioni quotate sono un tipo particolare di proiezioni ortogonali e consistono in un metodo di
rappresentazione utilizzato principalmente in topografia.
77
Dette anche Proiezioni topografiche, queste si basano principalmente su due operazioni fondamentali:
•
•
sezioni multiple dell'oggetto da rappresentare, con un numero adeguato di piani paralleli ed
equidistanti tra loro;
proiezione ortogonale di tali sezioni su un piano di riferimento, anch'esso parallelo ai precedenti,
detto piano di quadro.
Le figure geometriche generate sul quadro da queste operazioni (in genere curve) sono dette isoipse o curve
di livello. Ad ognuna di esse viene associata una quota rispetto ad un piano di riferimento, o allorché trattasi
di oggetti geografici la quota rispetto al livello del mare
Teoria delle ombre
La teoria delle ombre è una parte della geometria descrittiva che si occupa di rappresentare, oltre ad un
solido, l'ombra prodotta dal solido rispetto ad alcune fonti di luce. La teoria dell’ombra, è uno degli argomenti
più completi e fondamentali della geometria descrittiva. la sua osservazione in natura permette allo studente
architetto di comprendere la maggior parte dei concetti della geometria descrittiva. Quali le classificazioni dei
metodi di proiezione, i problemi di incidenza, la corrispondenza biunivoca … ecc. L'ombra prodotta da un
solido viene rappresentata come la proiezione del solido rispetto ad una stella di rette (l'equivalente nello
spazio del fascio di rette). Per fonti di luce puntiformi si considera la stella di rette avente centro in quel
punto; per fonti di luce "a distanza infinita" si considera la stella di rette parallele definita dal corrispondente
punto a infinito. I due casi rappresentano, approssimativamente, le ombre generate rispettivamente da una
lampada e dal Sole. La parte della superficie di un solido K non rivolta verso la fonte di luce è l'ombra
propria di K; le linee che separano la parte in ombra propria da quella in luce, si dicono "separatrici di
ombra" di K. la proiezione delle separatrici di ombra di K su un altro oggetto, dal centro di proiezione in
questo caso coincidente con la sorgente luminosa, si dice "ombra portata" di K. Si dice ombra autoportata
se tale proiezione cade sulla stessa superficie di K. Con riferimento ai tipi di proiezioni, l’ombra d un oggetto
può essere prodotta da una sorgente natural, approssimativamente impropria, e quindi può essere
paragonata alle proiezioni parallele, o può essere paragonata alle proiezioni centrale se la sorgente
luminosa è artificiali, cioè prodotta da un punto proprio. Con riferimento ai problemi di incidenza, l’ombra di
un oggetto può essere interpretata come incidenza tra I diversi enti geometrici (tra retta piano, tra piani, o tra
superficie e piano). Ovvero l’ombra può essere interpretata come incidenza di un ente di luce ( retta, piano o
superficie) passante per un ente oggettivo (punto, retta, figura) con l’ente che riceve l’ombra (superficie
piana o curva).
78
Archi, volte, cupole e coperture
VOLTE
Definizioni
Arco semplice
Volta a crociera
Volta a botte
Volta a padiglione
Tagliando una volta a botte su pianta rettangolare con due piani verticali passanti per i vertici opposti del
rettangolo di base si ottengono 4 elementi:
2 cappe o manti
2 unghie o fusi
L’unione di quattro cappe forma la volta a crociera
L’unione di quattro unghie forma la volta a padiglione
Cupola
La cupola è una volta a calotta con perfetta simmetria centrale, con base poligonale, circolare o ellittica e
profilo a semicerchio, parabola oppure ovoidale. La cupola più tipica è a base circolare. In caso di cupola
poligonale si dice che è costituita da fusi ciascuno dei quali corrispondenti ad un lato della base. Il significato
di cupola a volte è esteso anche a qualsiasi tipo di volta, che sia a vela, a spicchi concavi o convessi, specie
quando questa abbia importanza preminente nell'architettura dell'edificio. Una cupola in architettura è
79
edificata con conci trapezoidali detti cunei, i cui giunti (i sottili interspazi tra pietra e pietra o mattone e
mattone) sono orientati verso un unico centro. È possibile costruire una cupola anche in materiale laterizio,
anche senza ricorrere a speciali mattoni trapezoidali, tramite il ricorso a malta. La cupola, in geometria fa
parte in generale della famiglia delle quadriche. In particolare si tratta di superfici che hanno sia per direttrici
sia per generatrici delle coniche non degeneri. Nei casi più frequenti di coperture a volte, la cupole viene
ottenuta dal movimento rotatorio, sia circolare, sia ellittico, di un arco di conica delta intorno ad una retta
verticale, detta asse di rotazione, in cui l'asse e la curva siano tra loro complanari.
ELEMENTI DI UNA CUPOLA
La base su cui poggia la cupola può essere fatta di muri continui oppure da archi su piedritti. Quando la base
è cilindrica, l'imposta della cupola dovrà essere circolare, quando la base è prismatica, la cupola sarà del
tipo della volta a padiglione. In diversi casi la struttura di base non segue esattamente la forma della cupola,
allora si rende necessario introdurre una serie di elementi di raccordo detti pennacchi o trombe. Tra la
cupola vera e propria ed il perimetro di base viene a volte inserito il tamburo di forma cilindrica o prismatica
nel quale sono aperte ampie finestre. L'interno della cupola può essere inoltre illuminato da un foro posto in
sommità che può essere aperto, o chiuso da lucernaio, o sormontato da una lanterna, elemento di
coronamento a somiglianza di piccolo tempietto rotondo in genere finestrato. L'intradosso (la superficie
interna) di una cupola è sempre visibile, talvolta coperto da affreschi, stucchi o altre decorazioni. La luce
negli edifici a cupola può essere ottenuta anche con occhi aperti sulla superficie della calotta o con
finestrelle aperte sopra la linea di imposta.
T IPI DI CUPOLA
Dal punto di vista architettonico si può avere:
•
•
•
•
•
•
•
Cupola a padiglione o volta a padiglione: a base poligonale e costituita da vele che poggiano sui
lati del tamburo.
Cupola a ombrello o a spicchi: quando è costruita a partire da un sistema di archi diametrali (quindi
concentrici nella chiave di cupola)
Cupola estradossata: cupola la cui superficie esterna sia visibile e costituisca la copertura
dell'edificio stesso.
Cupola a bulbo o a cipolla: ha un corpo rialzato e strombato e una coronazione a punta, tipica
dell'architettura dell'Europa centrale e della Russia.
Cupola rialzata: tipica dell'architettura musulmana e indiana.
Cupola a cipolla: come la cupola a bulbo, ma dalla base molto stretta rispetto al corpo strombato
Cupole a grappolo: tipiche dell'architettura cristiana ortodossa
La cupola, come superficie viene, come di seguito, classificata secondo i tipi di coniche da cui sono formate
la generatrice e la direttrice di tale superficie.
•
•
•
•
•
•
•
•
Semisfera
Semi ellissoide circolare
Semi ellissoide ellittica
Semi parabolide circolare
Semi Parabolide ellittico
Semi iperbolide ad una falda circolare
Semi iperbolide ad una falda ellittico
Cupola geodetica
Arco
Aspetti base del comportamento strutturale
L’arco è un elemento strutturale in grado di incanalare, con la sua traiettoria curvilinea, le sollecitazioni
prodotte dai carichi trasformandole in forze prevalenti di compressione. La sollecitazione di compressione
rappresenta praticamente l’unica sollecitazione cui la pietra e la muratura sono in grado di resistere.
80
a tutto
sesto
a sesto ribassato
a sesto rialzato
Gli
archi
si realizzano
in genere
con mattoni comuni. La curvatura
a sesto acuto
ellittico
rampante
policentrico
zoppo
Gli archi si realizzano in genere con mattoni comuni. La curvatura è ottenuta creando dei giunti a forma di
cuneo: maggiore è il raggio di curvatura, minore è la differenza di larghezza del giunto fra intradosso ed
estradosso. La larghezza dei giunti è normalmente non inferiore a 5 mm nel punto più stretto e non superiore
a 20 mm nel punto più largo. La grande precisione dei mattoni estrusi rende molto evidente la forma a cuneo
dei giunti: questo aspetto è meno visibile negli archi con mattoni in pasta molle, meno regolari degli estrusi.
CENTINE La costruzione della centina comporta la creazione della forma curva prevista, sagomando un
singolo pannello di legno, se la luce è piccola, o costruendo una trave reticolare per luci maggiori. La faccia
superiore della centina può essere realizzata con stretti listelli di legno accostati; per carichi non elevati si
usano dei fogli di compensato inchiodati alla centina. Durante la costruzione delle centine vengono anche
fissati i centri di riferimento dai quali, con un filo o con un'asta in legno, potranno poi essere individuate le
direzioni dei giunti.
COSTRUZIONE DI UN ARCO A TUTTO SESTO
Per l’esecuzione occorre:
• segnare la posizione dei giunti ai lati del mattone di chiave e quindi dividere in spazi uguali un lato e poi
l’altro;
• posare un mattone per parte controllando sempre l’allineamento rispetto al centro;
• prima di inserire il mattone di chiave, stendere la malta sia sulle sue due facce che sui mattoni di
controchiave
81
COSTRUZIONE DI ARCHI RIBASSATI E PIATTABANDE
Per archi ribassati e piattabande è necessario posare ulteriori corsi di muratura oltre la linea d’imposta per
creare i piani d'imposta inclinati.
COSTRUZIONE DI ARCHI ELLITTICI
Il tracciamento della centina si effettua fissando una corda a due chiodi conficcati nei fuochi dell'ellisse (A e
B) e facendo scorrere sul pannello di compensato una matita che tenga la corda sempre tesa. Per segnare
la direzione dei giunti, fissare tra di lorocon dei perni quattro assicelle di uguale lunghezza in modo da
realizzare un rombo snodato. La corda impiegata per il tracciamento viene fatta passare per tre dei suoi
vertici in modo che il rombo, scorrendo lungo l'intradosso dell'arco, si adatti alle direzioni dei due rami della
corda: la diagonale del rombo indica la direzione del giunto.
Coperture
La copertura, o più comunemente tetto (ultimamente dal verbo latino tegere, oppure coprire), ha la funzione
di definire la parte superiore dell’edificio e di preservare l’ambiente interno dagli agenti atmosferici. Lo scopo
essenziale delle coperture è impedire l’insorgere di umidità, di opporre resistenza alle sollecitazioni date da
neve e vento e diminuire la dispersione termica dell'edificio. Il manto di copertura, che è lo strato esterno
delle coperture, garantisce la tenuta dell’acqua, mentre la struttura portante ha il compito di sostenere il
manto.
T IPI DI COPERTURA
In base ai materiali utilizzati per il manto le coperture sono così raggruppate:
COPERTURE DISCONTINUE
82
Il manto è effettuato con vari materiali che, grazie al modo in cui sono collegati e alla loro pendenza,
assicurano la tenuta dell’acqua. Le coperture discontinue sono a loro volta ripartite in:
•
•
•
•
•
•
•
•
•
•
•
coperture di tegole in laterizio;
coperture di tegole in cemento;
coperture di lastre in fibrocemento;
coperture di lastre in pietra (lose o beole);
coperture di lastre di materie plastiche;
coperture di tegole bituminose;
coperture di pannelli metallici coibentanti;
coperture di rame;
coperture di lamiere grecate di acciaio zincato, rame, alluminio, ecc,;
coperture di paglia;
coperture di canna lacustre.
COPERTURE CONTINUE
Il manto è attuato con elementi molto ampi congiunti insieme durante la posa in opera, in modo da
assicurare la tenuta per qualsiasi pendenza. Le coperture continue sono divise in:
•
•
•
•
coperture impermeabilizzate a freddo;
coperture impermeabilizzate a caldo;
coperture impermeabilizzate con membrane sintetiche;
coperture impermeabilizzate con membrane bituminose.
In base alla pendenza le coperture possono essere suddivise in:
•
•
tetti a falde, costituiti da una o più falde con pendenza diversa a seconda dei materiali usati per il
manto;
tetti piani, realizzati da pendenza minime ma commisurati per smaltire le acque.
Disegno per il progetto architettonico
Non tutti sono in grado di leggere i disegni tecnici che illustrano un progetto
edilizio, perché spesso questo è molto differente dall’idea che si ha dell’oggetto
che rappresenta, cioè l’edificio.
In architettura esistono tre tipi principali di rappresentazione, che sono quelle
bidimensionali, la pianta, la sezione verticale e il prospetto. A queste si
aggiungono forme ulteriori di rappresentazione geometrica, come l’assonometria e
la prospettiva.
I disegni architettonici sono immagini in scala dell’edificio che rappresentano.
Dire, ad esempio, che un disegno è in scala 1:100, significa che 1 cm sul disegno
rappresenta 100 cm al reale, cioè un metro. Le scale più frequentemente usate per il disegno edilizio sono
1:200, 1:100, 1:50 e 1:20.
La pianta è una proiezione ortogonale ottenuta tagliando l’edificio con un immaginario piano orizzontale.
Esa è sicuramente il disegno architettonico con cui si ha la maggiore dimestichezza: a tutti sarà capitato di
averne una tra le mani.
Quelle che sono presentate dai costruttori non sono fornite di tutte le indicazioni tecniche dettagliate, ma
servono ad illustrare la disposizione dei vari locali, la dimensione e la posizione delle varie aperture. Una
pianta completa dà, invece, la possibilità di valutare molti altri aspetti. Innanzitutto ci dà maggiori
83
informazioni su alcuni caratteri costruttivi dell’edificio, come la dimensione e la posizione dei pilastri, lo
spessore dei muri perimetrali, lo spessore dei muri che separano i vari locali, detti comunemente tavolati o
tramezzi.
Sono poi indicate le dimensioni dei vari elementi, quindi le misure in lunghezza e larghezza dei locali e le
superfici indicate al centro in metri quadrati. Le dimensioni in altezza e larghezza dei serramenti sono
indicate lungo la linea di mezzeria delle porte, mentre il senso di apertura è indicato con un arco di cerchio.
Su una pianta è possibile anche dare tutte le informazioni che riguardano l’impiantistica, come la posizione
degli scarichi delle acque bianche e nere, la posizione della canna fumaria, dei radiatori, di interruttori,
prese di corrente e punti luce.
Sulla pianta possono essere inoltre indicati riferimenti ai materiali usati e note che rimandano a disegni di
dettaglio. In particolare sono segnate le linee di sezione.
La sezione verticale, rispetto alla pianta, è un disegno di
lettura meno immediata per un profano. Essa, in termini
pratici, rappresenta ciò che si vede tagliando idealmente
l’edificio con un piano verticale. In sezione sono indicate
tutte le misure verticali, dette in termini tecnici quote.
Si assume come punto di riferimento 0.00 la quota del
marciapiede, così andando verso l’alto le quote sono
precedute dal segno +, e andando verso il basso dal segno
-.
In sezione è anche possibile leggere il tipo di fondazioni adottate e il numero complessivo dei piani.
I prospetti sono le proiezioni ortogonali dove è più facile riconoscere l’aspetto dell’edificio, di cui vengono
riprodotte le facciate. Su di essi non sono in genere riportate misure ma piuttosto sono indicati i materiali
utilizzati e i colori. Le rappresentazioni tecniche descritte mostrano ciascuna degli aspetti parziali degli
edifici rappresentati. Una rappresentazione più realistica è quella costituita dai disegni tridimensionali.
N.B. Si consiglia anche lo studio delle metodologie di rappresentazione dei materiali
e quello delle misure di riferimento umane.
84
FISICA
Unità di misura delle grandezze fondamentali.
Sistema Internazionale di Unità di Misura (SI)
Lunghezza
L’unità di lunghezza è il metro (m).
Massa
L’unità di massa è il kilogrammo(kg
Intervallo di tempo
L’unità di intervallo di tempo è il secondo (s).
Intensità di corrente
Come grandezza elettrica fondamentale, in un primo tempo, fu fissata la carica elettrica la cui unità è il
coulomb (C), definita come la carica che una corrente elettrica di un ampere (A) trasporta in un secondo.
Successivamente, si preferì adottare direttamente l’ampere (A), definito come l’intensità di corrente costante
che, fluendo in due conduttori rettilinei, paralleli, infinitamente lunghi, di sezione circolare trascurabile, posti
nel vuoto alla distanza di un metro, determina tra essi la forza di 2 ・ 10−7 N per metro di lunghezza.
Altre grandezze del Sistema Internazionale di Unità di Misura
Alle unità elencate del (SI), vanno aggiunte:
- L’unità di temperatura, kelvin (K).
- Unità di quantità di sostanza: mole (mol).
- Unità di intensità luminosa, candela (cd).
- Unità di angolo piano: radiante (rad). Il radiante è l’angolo piano con il vertice nel centro di una
circonferenza, che sottende un arco di lunghezza uguale al raggio.
- Unità di angolo solido: steradiante (sr). Lo steradiante è l’angolo solido, con il vertice nel centro di una
sfera, che sottende una calotta sferica la cui area `e uguale a quella di un quadrato il cui lato ha la lunghezza
del raggio della sfera.
LAVORO ed ENERGIA
Il lavoro di una forza è il prodotto scalare della forza stessa per lo spostamento del corpo cui è applicata la
forza: dove L è il lavoro, F il vettore forza, S il vettore spostamento, ? l'angolo compreso tra i due vettori.
Poiché L=FS, L=Nm=joule; il lavoro di un joule è cioè quello compiuto da una forza costante di 1 N quando il
punto di applicazione della forza subisce lo spostamento di 1 m nella stessa direzione della forza. Se a un
corpo di massa m sul piano si applica una forza F, esso accelererà con accelerazione direttamente
proporzionale alla forza stessa, e si muoverà sl piano. Si supponga che: il corpo di massa m abbia una
velocità iniziale V?0 m/s; il vettore F sia costante (si produrrà quindi un'accelerazione a costante); il vettore S
sia parallelo a F, ossia che il corpo si sposti nella stessa direzione della forza. Per definizione è: L = FS cos
? Poiché l'angolo compreso tra i due vettori F e S è nullo (avendo i due vettori la stessa direzione), e
ricordando che, in modulo, F=ma e S=1/2at?+Vt, è: L = FS cos 0 = FS = ma(1/2at?+Vt) Ricavando t
dall'equazione V(t) = at+V del rettilineo uniformemente accelerato si ha: L = ma(1/2at?+Vt) = ma(1/2a (Vf -
85
V)?/a? + V (Vf - V)/a) = = ma (1/2 (Vf - V)?/a + V (Vf - V)/a) = m(1/2 (Vf - V) ? + V (Vf - V)) = = m(1/2
(Vf?+V?-2VfV) + VfV - V?) = m(1/2Vf? + 1/2V? - V?) = = m(1/2Vf? - 1/2V?) = 1/2mVf? - 1/2mV? Si ha quindi
che: dove L è il lavoro compiuto da un corpo di massa m con velocità iniziale V e velocità finale Vf. In
generale, un corpo possiede energia se è in grado di compiere un lavoro; l'unità di misura dell'energia è il
joule (N*m).
ENERGIA CINETICA
L'energia cinetica è l'energia posseduta da un corpo in movimento in grado di compiere un lavoro per effetto
della velocità posseduta. In generale, per un corpo di massa m dotato di velocità V?0 m/s vale l'espressione:
che esprime l'energia cinetica Ec posseduta da un qualsiasi corpo di massa m avente velocità V?0 m/s. Si
potrà anche scrivere: dove Ecf e Eci sono le energie cinetiche possedute da un corpo in due diversi istanti t.
Tale relazione esprime il teorema dell'energia cinetica: il lavoro compiuto dalla risultante delle forze applicate
a un corpo lungo una traiettoria AB è uguale alla variazione dell'energia cinetica subita dal corpo nel passare
da A a B. Si avrà in conclusione: ENERGIA POTENZIALE GRAVITAZIONALE.
ENERGIA POTENZIALE GRAVITAZIONALE
E` quella parte di energia correlata alla posizione in cui si trova il corpo rispetto ad un punto di riferimento
per cui l’energia potenziale viene posta a zero. Il suo valore e proporzionale all’altezza del corpo rispetto al
riferimento :
E q ·p = m·g·h
Quando un corpo cade, il valore della sua altezza diminuisce, e con esso la sua energia potenziale
gravitazionale. Cadendo il corpo acquista velocità: la sua energia potenziale gravitazionale si trasforma in
energia cinetica. L’energia potenziale gravitazionale esiste perche c’e la forza di gravità. Quando l’energia
potenziale gravitazionale di un corpo diminuisce (a causa di uno spostamento) e si trasforma in energia
cinetica si dice che la forza sta compiendo un lavoro. Il concetto di lavoro viene esteso a qualsiasi forza.
LAVORO
nella fisica il termine lavoro ha un significato preciso e cioè si parla di lavoro quando si è stato applicata una
forza ad un oggetto che si sposta nella direzione della forza. Più intensa è la forza, quindi, più è grande lo
spostamento e maggiore è il lavoro. In fisica non è il soggetto che compie il lavoro ma la forza stessa. Per
definizione si dice che il lavoro della forza Fv, dove per v s'intende vettore, è uguale al modulo della forza F
per il modulo S dello spostamento: L=F*S Le unità di misura sono in joule=N*m nel S.I., erg=dine*cm nel
C.G.S.; il lavoro di un joule è quindi quello compiuto dalla forza costante di un Newton quando il punto
d'applicazione della forza subisce nella sua stessa direzione lo spostamento di 1 m. Vale la trasformazione:
1 joule=N*m=107 erg Un'altra unità di misura è il kilogrammetro (kgpm) il lavoro compiuto dalla forza
costante di un kgp per spostare il punto di applicazione di un metro nella sua direzione. Esso è il lavoro di un
peso da un kg in caduta libera da 1 m. 1Kgpm=9,8N*m=9,8J La forza può anche essere di senso opposto
rispetto allo spostamento, in questo caso quindi: L=-F*S Quindi la forza può ostacolare come aiutare un
moto. Essa poi può non essere parallela allo spostamento ma inclinata di un angolo ? Definiamo lavoro della
forza Fv il prodotto della componente F1 di Fv secondo lo spostamento per il modulo di quest'ultimo: L=F1S
Quando la forza favorisce lo spostamento è chiamata motrice, quando lo ostacola invece è chiamata
resistente. La legge di cui sopra è però uguale a: L=FS1 Dove S1 è la proiezione ortogonale di S su F e
quindi detto ? l'angolo formato da Fv e Sv: L=F*S cos? Quando Fv e Sv sono perpendicolari il lavoro è nullo,
così come nel moto circolare uniforme dove la forza centripeta è sempre perpendicolare alla velocità e
quindi allo spostamento, rendendo il lavoro nullo. L'equazione per arrivare al lavoro è un prodotto scalare dei
vettori Fv e Sv: L=Fv X Sv Il lavoro di una forza è quindi il prodotto scalare della forza per lo spostamento e
quindi conoscendo le componenti della forza e dello spostamento si ha: L=FxSx + FySy
86
POTENZA
Per potenza s'intende il lavoro svolto da una forza in un secondo. Quindi la potenza media Pm in un
intervallo di tempo t è il rapporto tra il lavoro L compiuto da una o più forze durante l'intervallo di tempo t:
Pm= ?L/?t La potenza è la rapidità con cui si compie un lavoro. Se indichiamo con Fs la componente della
forza che produce lo spostamento e il lavoro ?L si può scrivere: P= Fs* ?S/?t Cioè: P=Fsv Le unità di misura
della potenza sono nel sistema SI il Watt (W)=J/s nel sistema C.G.S. erg/s.
La termodinamica è quella branca della fisica e della chimica (chimica fisica) che descrive le trasformazioni
subite da un sistema in seguito a processi che coinvolgono la trasformazione di materia ed energia. La
termodinamica classica si basa sul concetto di sistema macroscopico, ovvero una porzione di materia
fisicamente o concettualmente separata dall'ambiente esterno, che spesso per comodità si assume non
perturbato dallo scambio di energia con il sistema. Lo stato di un sistema macroscopico che si trova
all'equilibrio è specificato da grandezze dette variabili termodinamiche o di stato come la temperatura, la
pressione, il volume, la composizione chimica.
Variabili termodinamiche
la temperatura non costituisce una vera e propria grandezza fisica. La proprietà che il concetto di
temperatura intende quantificare può essere ricondotta essenzialmente a una relazione d'ordine fra i sistemi
termodinamici rispetto alla direzione in cui fluirebbe il calore se fossero messi a contatto. Per questo,
l'equivalente della scelta di un'(arbitraria) unità di misura per una grandezza fisica, corrisponde, per la
temperatura, alla scelta di un'(arbitraria) scala termometrica. L'arbitrarietà è maggiore, in questo caso, che in
quello dell'unità di misura per una grandezza fisica. Lì la relazione di trasformazione fra un'unità e un'altra
può essere solo proporzionale (il rapporto fra le due unità di misura considerate). In questo caso, invece,
una qualsiasi trasformazione monotona di una particolare scala termometrica scelta preserverebbe
comunque la relazione d'ordine e dunque costituirebbe un'alternativa del tutto legittima al problema di
quantificare la temperatura. Ecco perché, ad esempio, le scale termometriche di Celsius, di Kelvin e di
Fahrenheit, sono legate fra di loro da relazioni che includono costanti additive (e dunque non sono
proporzionali). L'unità base della temperatura nel Sistema Internazionale è il kelvin (simbolo: K). Un kelvin
viene formalmente definito come la frazione 1/273,16 della temperatura del punto triplo dell'acqua (il punto in
cui acqua, ghiaccio e vapore coesistono in equilibrio). Nelle applicazioni di tutti i giorni è spesso conveniente
usare la scala Celsius (scala centigrada), nella quale assume il valore di 0 °C corrisponde al punto di fusione
del ghiaccio e il valore di 100 °C corrisponde al punto di ebollizione dell'acqua a livello del mare.
In questa scala una differenza di temperatura di un grado è pari a 1 K; quindi la scala è essenzialmente la
stessa della scala kelvin, ma con uno scostamento alla temperatura a cui l'acqua congela di (273,15 K).
Un'altra scala usata spesso nei paesi anglosassoni è la scala Fahrenheit. Su questa scala il punto di
congelamento dell'acqua corrisponde a 32 °F e quello di ebollizione a 212 °F. La seguente formula può
essere usata per convertire i gradi Fahrenheit in gradi Celsius:
In fisica, in particolare in termodinamica, il calore è il trasferimento di energia termica tra un sistema e il suo
ambiente in virtù di una differenza di temperatura o di un cambiamento di fase. Quando il calore è associato
ad una variazione di temperatura prende il nome di calore sensibile, quando invece determina un
cambiamento di fase prende il nome di calore latente.
Il trasferimento (o scambio o propagazione) del calore tra sistemi può avvenire:
•
per conduzione: in uno stesso corpo o fra corpi a contatto si ha una trasmissione, per urti, di energia
cinetica tra le molecole appartenenti a zone limitrofe del materiale. Nella conduzione viene trasferita
energia attraverso la materia, ma senza movimento macroscopico di quest'ultima;
•
per convezione: in un fluido in movimento, porzioni del fluido possono scaldarsi o raffreddarsi per
conduzione venendo a contatto con superfici esterne e poi, nel corso del loro moto (spesso a
carattere turbolento), trasferire (sempre per conduzione) l'energia acquistata ad altre superfici,
dando così luogo ad un trasferimento di calore per avvezione. In un campo gravitazionale quale
quello terrestre (associato alla forza peso), tale modalità di trasferimento di calore, detta convezione
87
libera, è dovuta al naturale prodursi di correnti avvettive, calde verso l'alto e fredde verso il basso,
dovute a diversità di temperatura e quindi di densità delle regioni di fluido coinvolte nel fenomeno,
rispetto a quelle del fluido circostante;
•
per irraggiamento: tra due sistemi la trasmissione di calore può avvenire a distanza (anche nel
vuoto), per emissione, propagazione e assorbimento di onde elettromagnetiche: anche in questo
[5]
caso il corpo a temperatura inferiore si riscalda e quello a temperatura superiore si raffredda. Il
meccanismo dell'irraggiamento non richiede il contatto termico tra i corpi coinvolti nel processo.
In quanto energia, il calore si misura nel sistema Internazionale in joule. Nella pratica viene tuttavia ancora
spesso usata come unità di misura la caloria, che è definita come la quantità di calore necessaria a portare
la temperatura di un grammo di acqua distillata, sottoposta alla pressione di 1 atm, da 14,5 °C a 15,5 °C. A
volte si utilizzano anche unità a carattere meramente tecnico, quali kW h o BTU.
La pressione è una grandezza fisica, definita, come il rapporto tra il modulo della forza agente
[1]
ortogonalmente su una superficie e la superficie stessa. Il suo opposto (una pressione con verso opposto)
è la tensione meccanica.
La pressione è una grandezza intensiva e quindi si intende sempre riferita all'unità di superficie.I fluidi
risentono della pressione, mentre i solidi risentono della tensione. Pressione e tensione, nel caso in cui siano
interne ad un corpo, possono essere generalizzate nel concetto di sforzo meccanico. Il volume o capacità è
la misura dello spazio occupato da un corpo. Viene valutato ricorrendo a molte diverse unità di misura.
3
L'unità adottata dal Sistema Internazionale è il metro cubo, simbolo m . Il volume di un oggetto solido è un
valore numerico utilizzato per descrivere a 3 dimensioni quanto spazio occupa il corpo. Ad oggetti ad una
dimensione (come una linea) o a 2 dimensioni (come un quadrato) si assegna per convenzione volume 0 in
uno spazio tridimensionale. Matematicamente i volumi sono definiti mediante l'applicazione di calcolo
integrale, come se il corpo fosse formato dalla somma di una grandissima quantità di piccoli cubi. La
generalizzazione di volume, arbitrariamente esteso a più dimensioni, viene chiamato contenuto.
T RASFORMAZIONI TERMODINAMICHE
Quando un sistema passa da uno stato di equilibrio ad un altro, si dice che avviene una trasformazione
termodinamica: si distingue tra trasformazioni reversibili, ovvero quelle trasformazioni che consentono di
essere ripercorse in senso inverso (si ritorna precisamente al punto di partenza, ripercorrendo all'indietro gli
stessi passi dell'andata), e trasformazioni irreversibili, ovvero quelle trasformazioni che, se ripercorse
all'indietro, non faranno ritornare al punto iniziale, ma ad uno diverso. Perché una trasformazione sia
reversibile è necessario che essa avvenga abbastanza lentamente da permettere al sistema di termalizzare
(il sistema deve passare attraverso infiniti stati di equilibrio termodinamico). Le trasformazioni
termodinamiche possono essere anche dei seguenti tipi:
•
•
•
•
•
Isobare: se la pressione si mantiene costante;
Isocore, se il volume si mantiene costante (e il lavoro scambiato tra sistema ed esterno è dunque
nullo);
Isoterme, se la temperatura si mantiene costante;
Adiabatiche, se il calore totale scambiato è nullo;
Isoentropiche, o adiabatiche reversibili, se la variazione di entropia è nulla
PRINCIPI DELLA TERMODINAMICA
I principi della termodinamica regolano le trasformazioni termodinamiche, il loro procedere, i loro limiti. Sono
dei veri e propri assiomi, non dimostrati e indimostrabili, fondati sull'esperienza, sui quali si fonda tutta la
teoria che riguarda la termodinamica.
Si possono distinguere tre principi di base
88
PRIMO PRINCIPIO: Quando un corpo viene posto a contatto con un altro corpo relativamente più freddo,
avviene una trasformazione che porta a uno stato di equilibrio, in cui sono uguali le temperature dei due
corpi. Per spiegare questo fenomeno, gli scienziati del XVIII secolo supposero che una sostanza, presente in
maggior quantità nel corpo più caldo, passasse nel corpo più freddo. Questa sostanza ipotetica, detta
calorico, era pensata come un fluido capace di muoversi attraverso la materia. Il primo principio della
termodinamica invece identifica il calore come una forma di energia che può essere convertita in lavoro
meccanico ed essere immagazzinata, ma che non è una sostanza materiale. È stato dimostrato
sperimentalmente che il calore, misurato originariamente in calorie, e il lavoro o l'energia, misurati in joule,
sono assolutamente equivalenti. Ogni caloria equivale a 4,186 joule. Il primo principio è dunque un principio
di conservazione dell'energia. In ogni macchina termica una certa quantità di energia viene trasformata in
lavoro: non può esistere nessuna macchina che produca lavoro senza consumare energia. Una simile
macchina, se esistesse, produrrebbe infatti il cosiddetto moto perpetuo di prima specie. Il primo principio
viene tradizionalmente enunciato come "In un sistema chiuso si ha che:
∆U = Q - L
dove U è l'energia interna del sistema. Per energia interna si intende la somma delle energie cinetiche e di
interazione delle diverse particelle di un sistema. Q è il calore scambiato tra ambiente e sistema (positivo se
fornito al sistema, negativo se invece ceduto dal sistema) e L il lavoro compiuto (positivo se compiuto dal
sistema sull'ambiente, negativo invece se compiuto dall'ambiente sul sistema). La convenzione dei segni
risente del legame con lo studio dei motori termici, nei quali il calore viene trasformato (parzialmente) in
lavoro.
SECONDO PRINCIPIO: Esistono diversi enunciati del secondo principio, tutti equivalenti, e ciascuna delle
formulazioni ne mette in risalto un particolare aspetto. Esso afferma che « è impossibile realizzare una
macchina ciclica che abbia come unico risultato il trasferimento di calore da un corpo freddo a uno caldo»
(enunciato di Clausius) o, equivalentemente, che « è impossibile realizzare una trasformazione il cui risultato
sia solamente quello di convertire in lavoro meccanico il calore prelevato da un'unica sorgente» (enunciato di
Kelvin). Quest'ultima limitazione nega la possibilità di realizzare il cosiddetto moto perpetuo di seconda
specie. L'entropia totale di un sistema isolato rimane invariata quando si svolge una trasformazione
reversibile ed aumenta quando si svolge una trasformazione irreversibile.
TERZO PRICIPIO: È strettamente legato al secondo, e in alcuni casi è considerato come una
conseguenza di quest'ultimo. Può essere enunciato dicendo che « è impossibile raggiungere lo zero
assoluto con un numero finito di trasformazioni» e fornisce una precisa definizione della grandezza
chiamata entropia. Esso afferma inoltre che l'entropia per un solido perfettamente cristallino, alla
temperatura di 0 kelvin è pari a 0. È facile spiegare questo enunciato tramite la termodinamica
molecolare: un solido perfettamente cristallino è composto da un solo complessioma (sono tutti i modi
di disporre le molecole, se le molecole sono tutte uguali indipendentemente da come sono disposte,
macroscopicamente il cristallo è sempre uguale) e, trovandosi a 0 kelvin, l'energia vibrazionale,
traslazionale e rotazionale delle particelle che lo compongono è nulla, per cui, dalla legge di Boltzmann
S = k ln(1) = 0 dove 1 sono i complessiomi (in questo caso uno solo).
I PASSAGGI DI STATO
Ogni sostanza può esistere in ognuno di questi stati e quindi può passare da uno stato ad un altro; questi
passaggi si chiamano appunto passaggi di stato.
I passaggi di stato hanno i seguenti nomi:
FUSIONE: PASSAGGIO DA SOLIDO A LIQUIDO
Vaporizzazione: passaggio da liquido ad aeriforme
Liquefazione: passaggio da aeriforme a liquido
Solidificazione: passaggio da liquido a solido
89
Sublimazione: passaggio diretto da solido ad aeriforme e viceversa (il passaggio inverso viene anche
chiamato brinamento).
I passaggi di stato sono fenomeni fisici, perché non danno luogo a cambiamenti nella composizione delle
sostanze interessate.
LEGGE DI ARCHIMEDE
Un corpo immerso (totalmente o parzialmente) in un fluido riceve una spinta (detta forza di galleggiamento)
verticale (dal basso verso l'alto) di intensità pari al peso di una massa di fluido di forma e volume uguale a
quella della parte immersa del corpo. Il punto di applicazione della forza di Archimede, detto centro di spinta,
si trova sulla stessa linea di gradiente della pressione su cui sarebbe il centro di massa della porzione di
fluido che si troverebbe ad occupare lo spazio in realtà occupato dalla parte immersa del corpo. Tale forza è
detta forza di Archimede o spinta di Archimede o ancora spinta idrostatica (nonostante non riguardi solo i
corpi immersi in acqua, ma in qualunque altro fluido – liquido o gas). La spinta si applica al baricentro della
massa di fluido spostata e non al baricentro della parte del corpo immersa nel fluido ed è diretta, secondo
l'equazione fondamentale dell'idrostatica, verso il piano dei carichi idrostatici (o piano a pressione relativa
nulla), che nella maggioranza dei casi coincide con il pelo libero del fluido, ed è quindi diretta verso l'alto.
CINEMATICA
Parte della Meccanica che studia il moto dei corpi senza tener conto delle cause che lo producono.
La velocità
È definita come spazio percorso nell'unità di tempo.
È una grandezza derivata
È una grandezza vettoriale
In un moto qualsiasi si può individuare una velocità media ed una velocità istantanea
La velocità istantanea è quella indicata dal tachimetro.
90
[m/s]
[m/s]
L'accelerazione
È definita come variazione di velocità nell'unità di tempo.
È una grandezza derivata
È una grandezza vettoriale
In un moto qualsiasi si può individuare un'accelerazione media ed un'accelerazione istantanea
2
[m/s ]
2
[m/s ]
MOTI RETTILINEI
Moto vario
È il caso più generale di moto.
La velocità varia ma può non esserci alcuna relazione spazio - tempo
In mancanza di una legge matematica si può solo calcolare la velocità media in un intervallo di tempo o di
spazio
Moto rettilineo uniforme
Si ottiene quando la velocità è rappresentata da un vettore costante.
v = cost
Se si pone s = 0 quando t = 0, cioè si pone la coordinata dello spazio a zero nel momento in cui si comincia
a contare i tempi, si possono scrivere le seguenti formule semplificate:
s = vt
v = s/t
t = s/v
Moto rettilineo uniformemente accelerato
Si ottiene quando un oggetto è sottoposto ad un vettore accelerazione costante e la sua velocità non ha
componenti perpendicolari all'accelerazione stessa
a = cost
Conviene distinguere due casi:
1) moto accelerato con partenza da fermo
Ponendo all'istante iniziale t = 0, v = 0 e, per semplicità, anche s = 0, otteniamo le seguenti relazioni scalari:
v = at
a = v/t
t = v/a
Velocità e accelerazione hanno sempre lo stesso verso.
91
2) moto accelerato con velocità iniziale
Nell'istante in cui si comincia a contare il tempo, t = 0, l'oggetto possiede una velocità v = v0, per semplicità,
in questo istante, considereremo ancora s = 0.
Espressione della velocità:
v = v0 + at
Moto circolare uniforme
Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in
modulo, intensità) costante si dice moto circolare uniforme. Si noti che ad essere costante, in questo moto,
è l'intensità della velocità, cioè il numero che ne rappresenta il valore. Questa precisazione è doverosa,
perché in questo moto la direzione della velocità cambia continuamente. La velocità, come ben sappiamo, è
un vettore per cui è caratterizzata da intensità, direzione e verso. La velocità, come ben sappiamo, è un
vettore per cui è caratterizzata da intensità, direzione e verso.
Definiamo (o ridefiniamo più esattamente) ora alcune grandezze relative al moto circolare uniforme :
Periodo Il periodo è il tempo impiegato a fare un giro completo. Esso si misura nel S.I. (Sistema
Internazionale) in secondi. Esso viene di solito indicato dalla lettera maiuscola T .
Frequenza La frequenza indica il numero di giri completi effettuati nell'unità di tempo. Nel S.I.
la frequenza si misura in hertz (Hz) ed indica il numero di giri al secondo. Essa di solito indicata con la
lettera minuscola f o la lettera greca ν ("ni"). La frequenza caratterizza in generale un fenomeno periodico
qualunque. Fra il periodo e la frequenza sussiste una relazione matematica importantissima :
f = 1 / T che esprime il fatto che la frequenza è l'inverso del periodo.
Velocità scalare
La velocità scalare del moto circolare uniforme è, come per tutte le velocità, misurata dal rapporto spazio /
tempo . Se il raggio della circonferenza è R , considerando che l'intera circonferenza misura 2 π R e che il
tempo complessivo per percorrerla è il periodo T , si avrà allora :
v=s/t=2πR/T
Questa è la formula della velocità scalare del moto rettilineo uniforme.
Accelerazione centripeta
Il moto rettilineo uniforme è un moto dotato di accelerazione perché la direzione della sua velocità cambia
punto per punto. Vediamo ora come si calcola questa accelerazione e le sue caratteristiche.
Moto oscillatorio armonico
Il moto oscillatorio armonico e un moto periodico, determinato dalla proiezione P1, sul diametro della
circonferenza, di un punto P che si muove di moto circolare uniforme.
92
DINAMICA
La dinamica è il ramo della meccanica che si occupa dello studio del moto dei corpi e delle sue cause o, in
termini più concreti, delle circostanze che lo determinano e lo modificano. Lo studio completo della
meccanica comprende anche la statica e la cinematica: la dinamica si differenzia dalla prima che studia le
configurazioni di equilibrio meccanico, dalla seconda che studia, in astratto, tutti i moti concepibili ma non si
occupa di determinare quali moti possono avvenire in un determinato contesto sperimentale.
Primo principio
Questa legge è nota anche con il nome di principio di inerzia Oggi il principio viene così formulato: Se un
corpo è soggetto ad un sistema di forze a risultante zero, allora rimane in quiete o in moto rettilineo
uniforme. Tale corpo si dirà in equilibrio
Secondo principio o legge di Newton
L'accelerazione di un corpo è proporzionale alla forza risultante esercitata sul corpo e usando una
simbologia moderna, questa legge può essere espressa dall'equazione:
essendo p = m v la quantità di moto di un corpo di massa m che si muove con velocità v rispetto
all'osservatore e ∆ p la sua variazione, mentre Fm è la forza media che agisce nell' intervallo di tempo ∆ t.
Terzo principio
Ad ogni azione corrisponde una reazione uguale e contraria. Questa legge è anche nota con il nome di
principio di azione e reazione. Essa riconosce in primo luogo il fatto che le forze nascono sempre dall'
interazione tra due corpi. Se su un sistema formato da due corpi non agiscono forze esterne, risulta
Altre forze
Si definisce forza quella grandezza fisica derivata, espressa da un vettore, caratterizzata quindi da una
direzione, un verso e un'intensità, capace di modificare lo stato di un corpo.
Il peso, ad esempio, è la forza che agisce su un corpo a causa della sua massa in un campo gravitazionale
(come ad esempio l’atmosfera terrestre).
Tra le forze va considerata anche la forza di attrito Fa. Trascinando un corpo su un piano, non è mai stato
considerato l’attrito che sussiste tra corpo e piano, attrito che invece esiste e che si modellizza come una
forza applicata in direzione opposta allo spostamento, con modulo pari al prodotto della componente della
forza perpendicolare al piano e il coefficiente K di attrito, specifico per ogni materiale (tale coefficiente e una
grandezza adimensionale e si distingue per ogni materiale in coefficiente di attrito statico Ks e dinamico Kd,
per i quali vale sempre Ks> Kd; e intuitivo che Fas > Fad, infatti e necessario applicare una forza maggiore
per mettere in moto un corpo fermo, piuttosto che mantenerlo in moto).
93
LA LEGGE DI GRAVITAZIONE UNIVERSALE (O LEGGE DI NEWTON)
La legge di gravitazione universale afferma che due punti materiali si attraggono con una forza di intensità
direttamente proporzionale al prodotto delle masse ed inversamente proporzionale al quadrato della
distanza che li separa. Questa legge, espressa vettorialmente, diventa:
dove
è la forza con cui l'oggetto 1 è attratto dall'oggetto 2, G è la costante di gravitazione universale,
-11
-2
che vale circa 6,67 × 10 Nm²kg , m1 e m2 sono le masse dei due corpi, e
, dove gli indici si
riferiscono alle due masse.
STATICA
La statica si occupa dell’equilibrio dei corpi: un corpo e in equilibrio quando il suo stato di moto si mantiene
costante nel tempo.
Punto materiale
E` un corpo di dimensioni nulle, ma di massa definita, posizionato in un preciso punto dello spazio.
Condizione necessaria e sufficiente affinché il corpo permanga nel suo stato di quiete (condizione di
equilibrio) e che la risultante delle forze ad esso applicate sia nulla.
Corpo esteso
Per descriverne la condizione di equilibrio di un corpo esteso e necessario, oltre a garantire le precedenti
condizioni, introdurre una nuova grandezza vettoriale: il momento. L’equilibrio sarà quindi dato da:
n
n
∑ Fi = 0
∑ Fi = 0
i=1
e
Queste formule rappresentano le due equazioni fondamentali della statica
Momento di una forza rispetto a un punto e la coppia di forze
- Il momento di una forza rispetto ad un punto corrisponde alla capacità di una forza di generare una
rotazione rispetto al punto chiamato polo. Il modulo del momento si calcola come il prodotto tra la forza e la
distanza tra la direzione della forza ed il punto di rotazione (tale distanza e chiamata braccio: b).
M = F ·b
La direzione del momento e perpendicolare al piano formato dal braccio e dalla forza e il verso si trova con
la regola della mano destra.
94
- Il momento di una coppia di forze (un sistema composto da due forze parallele, di modulo e direzione
uguale, ma di verso opposto) e dato dalla formula:
M = F ·b
essendo F uguale a una delle due forze e b la distanza tra le due forze (detto braccio della coppia).
Baricentro Ogni sistema di forze e uguale, dal punto di vista statico, ad un sistema composto dalla forza
risultante di tutte le forze e da un opportuno momento. Il punto di applicazione della risultante di tutte le forze
prende il nome di baricentro. Considerando, quindi, un corpo di massa M, diviso in tante piccole parti di
massa m, ciascuna delle quali soggetta alla forza peso, il baricentro corrisponderà al centro di gravità. Il
baricentro e dunque il punto in cui si può immaginare concentrato tutto il peso del corpo o di un sistema
formato da più corpi.
Leva La leva e una macchina costituita da un’asta rigida che può ruotare intorno ad un asse ad essa
perpendicolare. Il punto di incontro fra asse e leva e detto fulcro. La condizione di equilibrio delle leve si
ricava dalle equazioni fondamentali della statica:
F1 · b1 = F2 · b2
In base alla posizione reciproca del fulcro e delle forze le leve si distinguono in:
•
leve di primo genere: il fulcro si trova tra le due forze (interfulcrate); possono essere vantaggiose,
svantaggiose o indifferenti;
•
leve di secondo genere: la forza resistente si trova tra fulcro e forza applicata (o
potenza)(interresistente); sono sempre vantaggiose;
•
leve di terzo genere: la forza applicata (potenza) si trova tra fulcro e forza resistente (interpotente);
sono sempre svantaggiose.
95
MATEMATICA
NUMERI
NUMERI NATURALI
Vi sono differenti tipi di numeri. Quelli maggiormente conosciuti sono i numeri naturali
usati per contare, il cui insieme è indicato con N. La presenza dello zero fra i numeri naturali dipende dalla
convenzione scelta. Lo zero è comunque previsto dagli assiomi di Peano.
NUMERI INTERI RELATIVI
Se si introducono la differenza di segno e lo zero, distinguendo tra numeri positivi e numeri negativi, si
ottengono i numeri interi relativi (o semplicemente interi), il cui insieme è indicato con Z:
NUMERI RAZIONALI
Se i numeri interi vengono utilizzati per definire un rapporto, si ottengono i numeri razionali, cioè esprimibili
tramite una frazione (ratio in latino). Ad esempio:
L'insieme di tutti i numeri razionali è definito col simbolo Q.
NUMERI ALGEBRICI
I numeri algebrici sono tutti i numeri ottenibili come radici di equazioni algebriche a coefficienti interi. I numeri
razionali sono tutti algebrici, ma molti numeri algebrici non sono razionali. Ad esempio:
sono numeri algebrici che non possono essere descritti tramite una frazione.
Un numero non algebrico è detto trascendente. Ad esempio, π (pi greco) ed e sono trascendenti: non è
possibile ottenere π come radice di un polinomio a coefficienti interi.
NUMERI REALI
L'insieme dei numeri reali comprende tutti i numeri esprimibili, con o senza la virgola, tramite il sistema
numerico decimale. I numeri reali comprendono tutti i numeri elencati precedentemente. In particolare i
numeri reali si dividono in razionali e irrazionali, oppure in algebrici e trascendenti.
L'insieme dei numeri reali è simboleggiato con R.
96
NUMERI COMPUTABILI
Sono i numeri reali esprimibili con una notazione posizionale in una qualche base e sono costituiti da una
sequenza finita di cifre o da una successione illimitata di cifre che può essere generata da una procedura
ben definita in grado operare illimitatamente.
NUMERI COMPLESSI
L'insieme dei numeri reali non è sufficiente a fornire tutte le soluzioni delle equazioni algebriche. Per
esempio, l'equazione
non ha soluzioni nel campo dei numeri reali, perché in questo insieme il quadrato di un numero è sempre
positivo. Per risolvere questo problema, è stata introdotta l'unità immaginaria i, tale che
Tale numero non appartiene all'insieme dei numeri reali, bensì all'insieme dei numeri complessi. Più in
generale, un numero complesso è una espressione del tipo
dove i è l'unità immaginaria e a,b sono numeri reali. L'insieme dei numeri complessi è indicato con C.
OPERAZIONI ARITMETICHE
Le operazioni aritmetiche tradizionali sono addizione, sottrazione, moltiplicazione e divisione, sebbene
vengano a volte incluse nella materia anche operazioni più avanzate come l'elevamento a potenza,
l'estrazione di radice, i logaritmi e l'uso delle percentuali.
Addizione
Per l'addizione sono valide le seguenti proprietà:
•
la proprietà commutativa, la quale afferma che cambiando l'ordine degli addendi il risultato non
cambia:
a+b=b+a
•
la proprietà associativa, la quale afferma che sostituendo due addendi con la loro somma il risultato
non cambia:
a + b + c = (a + b) + c = a + (b + c)
PROPRIETÀ INVARIANTIVA DELLA SOTTRAZIONE
Aggiungendo uno stesso termine al minuendo e al sottraendo la differenza non cambia:
A-B=C
(A + D) - (B + D) = C
97
Moltiplicazione
Proprietà commutativa
Non ha importanza l'ordine con cui vengono moltiplicati due numeri. Infatti, per ogni coppia di numeri
x e y,
È importante sottolineare che questa proprietà vale solo per i numeri (interi, razionali, reali,
complessi), ma non vale sempre, ad esempio non vale quando si moltiplicano tra loro matrici e
quaternioni.
Proprietà associativa
Per ogni terna di numeri x, y e z,
cioè non è importanza l'ordine con cui vengono eseguite le operazioni se queste coinvolgono solo le
moltiplicazioni.
Proprietà distributiva rispetto all'addizione
Si può "distribuire" la moltiplicazione ai vari addendi di una somma:
Divisione
Invariantiva: a : b- (a: c) : (b: c) – (a : c) : (b – c) se c ≠ 0
Distributiva rispetto alla somma e alla sottrazione: (a+b) : c - a : c + b : c
MCD (Massimo Comune Divisore):
e il più grande fra tutti i numeri interi positivi che dividono tutti i numeri dati. Come si calcola: si scompongono
i numeri dati in fattori primi, quindi si moltiplicano i fattori comuni con il minimo esponente.
Es. MCD (24; 144; 60) = 12
24 = 23 ・ 3
144 = 24 ・ 32
60 = 22 ・ 3 ・ 5
MCD = 22 ・ 3 = 12
mcm (Minimo Comune Multiplo):
e il più piccolo multiplo di tutti i numeri dati tra i numeri interi positivi. Come si calcola: si scompongono i
numeri dati in fattori primi, quindi si moltiplicano i fattori comuni e non comuni con massimo esponente.
Es. mcm (24; 144; 60) = 720
98
24 = 23 ・ 3
144 = 24 ・ 32
60 = 22 ・ 3 ・ 5
OPERAZIONI FRA FRAZIONI
MOLTIPLICAZIONE E DIVISIONE
Le operazioni più semplici da compiere con le frazioni sono la moltiplicazione e la divisione. Ecco come
vengono effettuate tali operazioni. Se abbiamo tre persone che ottengono ciascuna un quarto di torta finiamo
col distribuirne tre quarti. Numericamente, possiamo scrivere:
Facendo un altro esempio, supponiamo che cinque persone lavorino tre ore al giorno su un progetto, e la
loro giornata lavorativa sia di sette ore. In totale, avranno lavorato per 15 ore, cioè 15 settimi di giorno. Dato
che 7 settimi di giorno sono un giorno intero, in totale avranno lavorato per 2 giorni e un settimo:
numericamente,
Riprendendo la nostra torta, se ne abbiamo preso un quarto e di questa vogliamo prenderne un terzo, ne
otterremo un dodicesimo. Infatti facciamo tre parti uguali della nostra fetta e ne prendiamo una: ma se
avessimo diviso in tre parti tutte e quattro le fette iniziali saremmo arrivati a quattro volte tre fette, cioè 12
fette. In altre parole, un terzo di un quarto (o "un terzo di volte un quarto") è un dodicesimo. Numericamente
abbiamo :
Come secondo esempio, supponiamo che i nostri cinque tizi abbiano fatto un lavoro che in totale equivale a
tre ore di una giornata lavorativa di sette ore. Ciascuno di loro - ammesso che abbiano lavorato con la
stessa lena! - ha fatto un quinto del totale, quindi hanno lavorato per un quinto di tre settimi di una giornata.
Numericamente,
In pratica, si può notare come per moltiplicare due frazioni possiamo semplicemente moltiplicare i due
numeratori tra loro, e i due denominatori tra loro, e usare i risultati come rispettivamente numeratore e
denominatore del prodotto. Ad esempio:
È possibile che il numeratore di una frazione e il denominatore dell'altra abbiano un fattore comune: in
questo caso è possibile (prima o dopo avere eseguito i due prodotti) semplificare il risultato, dividendo
entrambi i valori per il loro massimo comun divisore e riducendo così la frazione "ai minimi termini". Ad
esempio,
99
Se una o entrambe le frazioni da moltiplicare sono improprie, è più agevole convertire la frazione impropria
in una propria. Per esempio:
Il sistema più semplice di dividere due frazioni tra di loro è moltiplicare la prima frazione per l'inverso della
seconda. Nel caso più semplice di divisione di una frazione per un intero, avremmo così
ADDIZIONE E SOTTRAZIONE
La regola per l'addizione (o per la sottrazione) di due frazioni è più complicata; anche qua può essere utile
tornare all'esempio della torta per ricavare la regola generale. Se due torte uguali sono tagliate
rispettivamente in quattro e cinque parti e io prendo una fetta di ciascuna, quanta parte di torta ho?
Immaginiamo di dividere ciascuna fetta della prima torta in altre cinque parti uguali, e ciascuna fetta della
seconda torta in quattro parti uguali. A questo punto ho diviso entrambe le torte in
parti; di
queste ne ho cinque dalla prima torta e quattro dalla seconda, per un totale di nove fettine. Numericamente,
.
La formula generale per sommare due frazioni è data da
Se il massimo comun divisore M tra b e d è maggiore di 1, è possibile semplificare l'operazione. Posto
e
, abbiamo infatti che
;
si noti che il denominatore Mb'd' è il minimo comune multiplo dei denominatori b e d. Un esempio numerico è
.
COMMUTATIVITÀ
È importante ricordare che la moltiplicazione gode della proprietà commutativa, il che significa
semplicemente che l'ordine dei fattori non conta, e tre volte un quarto è uguale a un quarto di tre;
numericamente:
PROPORZIONI TRA GRANDEZZE OMOGENEE
Si dicono omogenee due grandezze appartenenti allo stesso insieme per le quali e possibile stabilire un
criterio di uguaglianza e disuguaglianza. Tra queste grandezze sono definite le operazioni di addizione e di
sottrazione, con le consuete proprietà formali.
100
PROPRIETA` DELLE PROPORZIONI
Se quattro numeri sono in proporzione, il prodotto del primo con il quarto è uguale al prodotto del secondo
con il terzo. In altre parole: in ogni quaterna proporzionale il prodotto dei medi è uguale al prodotto degli
estremi. In formula
Da questa proprietà ne derivano altre:
1. Regola del quarto proporzionale
Noti tre numeri a,b,c, il quarto proporzionale, d, tale che
, è dato da
Similmente si hanno le formule
2. Proprietà dell’invertire
Data una quaterna proporzionale, se ne ottiene un’altra scambiando tra loro ogni antecedente con il proprio
conseguente:
3. Proprietà del permutare
Data una quaterna proporzionale se ne ottiene un’altra scambiando tra loro o i medi o gli estremi:
4. Proprietà del comporre
In ogni quaterna proporzionale la somma degli antecedenti sta alla somma dei conseguenti come ogni
antecedente sta al proprio conseguente:
5. Proprietà dello scomporre
In ogni quaterna proporzionale la differenza degli antecedenti sta alla differenza dei conseguenti come ogni
antecedente sta al proprio conseguente:
Quando i due medi di una quaterna proporzionale coincidono, cioè quando
101
il loro comune valore è la media geometrica dei due estremi. Il numero 'b' è la parte media proporzionale fra i
numeri 'a' e 'd' . Proporzioni di questo tipo sono dette continue.
POTENZE
In matematica la potenza è un'operazione che associa ad una coppia di numeri a e n - detti rispettivamente
base ed esponente - il numero dato dal prodotto di n fattori uguali ad a:
in questo contesto a può essere un numero intero, razionale o reale mentre n è un numero intero positivo,
cioè appartiene a (numeri naturali).
Le seguenti proprietà sono di immediata verifica nel caso in cui gli esponenti siano numeri interi positivi:
•
Il prodotto di due, o più potenze aventi la stessa base, è una potenza che ha per base la stessa
base e come esponente la somma degli esponenti.
•
Il quoziente di potenze che hanno la stessa base è una potenza che ha per base la stessa base e
come esponente la differenza tra l'esponente del dividendo e l'esponente del divisore
•
La potenza di una potenza è una potenza in cui la base rimane la stessa e l'esponente è dato dal
prodotto degli esponenti:
•
il prodotto di potenze con lo stesso esponente è una potenza che ha per esponente lo stesso
esponente e per base il prodotto delle basi:
•
Il quoziente di potenze con lo stesso esponente è una potenza che ha per esponente lo stesso
esponente e per base il quoziente delle basi:
Notiamo che la definizione a0 = 1 risulta ora più comprensibile poiché è consistente con le proprietà appena
viste, infatti:
E lo stesso vale per la definizione di a − k, infatti:
102
RADICALI
Il radicale algebrico n a e ogni numero reale la cui potenza n-esima e uguale al numero reale a , dove a e il
radicando e n l’indice della radice appartenente ad N.
Prodotto Es. √3 · √2 = √6
Quoziente Es. ³√15 =³
√ 15 = ³√5
³√3
Potenza Es. (√8)³
Radice Es.
3
=
√3√ 64 =
√(8)³ =√ 512
6√
64 = 2
Attenzione: E possibile sommare solo radicali simili ovvero radicali che hanno uguali il radicando e l’indice
della radice. La loro somma algebrica e un radicale, ad essi simile, avente per coefficiente la somma
algebrica dei coefficienti.
Es. ³√ 5 + ³√5 = 2√5
ELEVAMENTO A POTENZA DI UN RADICALE
Per elevare a potenza una radice n-esima alla m, bisogno elevare il radicale alla m, dunque svolgere la
radice n-esima del numero trovato.
CASI PARTICOLARI
•
La radice n-esima di zero è uguale a zero, perché zero, elevato ad n, è uguale a zero
RAZIONALIZZAZIONE
Nelle elaborazioni di espressioni e formule algebriche, è spesso utile manipolare i radicali usando le relazioni
scritte sopra, senza tentare di calcolare il valore di ogni singolo elemento. Ad esempio, se a e b sono due
numeri positivi distinti:
,
L'ultima relazione può servire per razionalizzare il denominatore di un'espressione o di un'equazione
LOGARITMI
Si dice logaritmo in base a di un numero x l'esponente da dare ad a per ottenere x (x viene chiamato
argomento del logaritmo). In altre parole, se
103
segue che:
(si legge: y è il logaritmo in base a di x).
4
Per esempio, log3 81 = 4 perché 3 = 81.
PROPRIETÀ DEI LOGARITMI
•
Il logaritmo in base a di a è 1:
•
Il logaritmo di 1 è, in qualsiasi base, 0:
•
Vale l' identità:
•
Il logaritmo del prodotto di due numeri è uguale alla somma dei logaritmi dei due numeri:
•
Il logaritmo di un quoziente è uguale alla differenza tra i logaritmi del dividendo e del divisore:
•
Il logaritmo dell'inverso di a è l'opposto del logaritmo di a:
•
Il logaritmo di un numero elevato all'esponente k è uguale al prodotto dell'esponente per il logaritmo
del numero:
•
Il logaritmo della radice k di x è uguale al quoziente tra il logaritmo e k:
LOGARITMI DECIMALI E LOGARITMI NATURALI
I logaritmi decimali hanno come base il numero 10 e si indicano con la scrittura:
Logx che equivale a log10 x
104
I logaritmi naturali o Neperiani hanno come base un numero irrazionale, detto numero di Nepero (o Eulero),
indicato con la lettera e, il cui valore approssimato e: e = 2,71828…
I logaritmi naturali si indicano con la scrittura:
lnx che equivale a loge x
Le tavole dei logaritmi in base 10 (simbolo Log o log10 ) e in base e (simbolo ln) sono memorizzate in
qualsiasi calcolatrice scientifica.
MONOMI E POLINOMI
Si chiama monomio un’espressione algebrica, numerico-letterale, nella quale figurano solo operazioni di
moltiplicazione, di divisione e di elevamento a potenza. Un monomio si dice ridotto a forma normale quando
e un prodotto di un (solo) fattore numerico, detto coefficiente, e di potenze a basi letterali diverse. Due
monomi si dicono simili quando hanno uguale parte letterale; in tal caso la loro somma e un monomio ad
essi simile, avente per coefficiente la somma algebrica dei coefficienti. L’esponente di ogni variabile e il
grado del monomio relativo a quella variabile, mentre il grado complessivo di un monomio e la somma degli
esponenti che in esso compaiono.
Es. 2 · a3 ·b6
2 è il coefficiente numerico
a3 · b6 è la parte letterale
grado del polinomio = 3 + 6
Si chiama polinomio una somma algebrica di monomi. Un polinomio si dice ridotto a forma normale quando
i suoi termini sono ridotti a forma normale e fra essi non vi sono monomi simili. Si definisce grado
complessivo di un polinomio il massimo grado complessivo dei suoi termini. La somma algebrica di due o più
polinomi e il polinomio ottenuto dalla somma algebrica dei suoi termini. Il prodotto di due polinomi e il
polinomio ottenuto mediante l’applicazione della proprietà distributiva della moltiplicazione rispetto alla
somma, ovvero il polinomio ottenuto moltiplicando ciascun termine dell’uno per tutti i termini dell’altro.
Proprietà fondamentale: principio di identità dei polinomi
Due polinomi in una variabile, entrambi di grado n , che assumono gli stessi valori per n +1 valori della
variabile, sono identici.
IDENTITA` ED EQUAZIONI
Siano A(x) e B(x) , due espressioni algebriche nella indeterminata x .
L’uguaglianza:
A(x) = B(x)
si chiama identità quando essa e verificata per qualsiasi valore attribuito alla x (esclusi gli eventuali valori
per cui le espressioni perdono significato), mentre si chiama equazione quando essa e verificata soltanto
per particolari valori attribuiti alla x .
I valori che verificano l’equazione (o, come si usa anche dire, che “soddisfano l’equazione”) si chiamano
soluzioni (o radici, o zeri) dell’equazione.
Si chiama grado di un’equazione il più alto fra i gradi dei suoi termini.
Es. 4x6 + 3x2y5 – xy + 5x3 è di grado 6
105
Per il teorema fondamentale dell’algebra: un’equazione di grado n ha sempre n soluzioni, non
necessariamente reali, non necessariamente distinte. Risolvere un’equazione significa trovarne tutte le
soluzioni. L’indeterminata si chiama incognita dell’equazione.
Principi di equivalenza
A=B
A + C = B + C detto anche principio del trasporto, perche permette di trasportare termini da una
parte all’altra dell’uguale cambiando loro di segno
A=B
A · C = B · C dove C ≠ 0 (Attenzione!)
Attenzione: una questione essenziale, relativa alla risoluzione delle equazioni, consiste nello stabilire a quale
insieme numerico debbano appartenere le soluzioni dell’equazione da risolvere. Ad esempio, se il problema
e di natura geometrica e la soluzione e la misura di un segmento, o un perimetro, o un’area, la soluzione
andrà cercata nell’insieme dei numeri non negativi, se invece il problema e d’ordine goniometrico, e la
soluzione riguarda il possibile valore del seno di un angolo, la soluzione dovrà cadere nell’intervallo [-1,1], …
EQUAZIONI DI PRIMO GRADO (O LINEARI)
Una equazione lineare, o equazione di primo grado, è un'equazione algebrica di primo grado, dove cioè il
grado massimo delle incognite è uno.
RISOLUZIONE
Quelle ad una sola incognita sono riconducibili (tramite le usuali regole dell'algebra elementare) alla
cosiddetta forma normale:
ax + b = 0
dove a e b sono numeri reali o complessi.
Se
allora trasportando b a secondo membro e dividendo per a si ottiene:
L'equazione di primo grado ammette dunque una e una sola soluzione, pari a
.
Se invece a = 0 allora l'equazione può essere impossibile o indeterminata.
Se infatti b = 0 allora
, divisione di risultato indeterminato. Per questo anche l'equazione è detta
indeterminata e il suo insieme delle soluzioni coincide con il dominio.
Ma se fosse
risulterebbe
, il che è impossibile. L'equazione è quindi detta impossibile perché non
ha soluzioni: il suo insieme delle soluzioni è infatti vuoto.
EQUAZIONI DI 2° GRADO (O QUADRATICHE)
In matematica, un'equazione di secondo grado o quadratica è un'equazione algebrica ad una sola
incognita x che compare con grado pari a 2, e la cui formula è riconducibile alla forma:
con
.
Le soluzioni delle equazioni di secondo grado, per il teorema fondamentale dell'algebra, sono sempre 2
eventualmente coincidenti, nel campo complesso. Nel campo reale invece l'equazione quadratica ammette 2
soluzioni, eventualmente coincidenti, oppure nessuna soluzione.
106
Sono poi particolarmente semplici da risolvere le cosiddette equazioni incomplete, dove alcuni coefficienti
sono pari a zero. Il grafico della funzione
nel piano cartesiano è una parabola.
EQUAZIONI QUADRATICHE INCOMPLETE
EQUAZIONE SPURIA
Si dice spuria un'equazione quadratica che manca del termine noto, ossia avente la forma:
Un'equazione di questo tipo si risolve facilmente tramite scomposizione:
Per la legge di annullamento del prodotto quest'equazione è equivalente alle due:
e
E in definitiva le sue soluzioni sono
e
EQUAZIONE PURA
Si dice equazione quadratica pura un'equazione polinomiale di secondo grado che manca del termine di
primo grado, cioè che è della forma:
Portando c al secondo membro e dividendo per a si ottiene:
Se
, l'equazione non ammette soluzioni reali (ma due soluzioni immaginarie); viceversa, se
l'equazione è risolta da:
,
EQUAZIONI COMPLETE
Un'equazione polinomiale di secondo grado viene detta equazione quadratica completa quando tutti i suoi
coefficienti sono diversi da 0. Essa viene risolta con il cosiddetto metodo del completamento del quadrato,
così chiamato perché si modifica l'equazione fino ad ottenere al suo primo membro il quadrato di un binomio
nella forma
. Anzitutto portiamo c al secondo membro:
Moltiplichiamo per 4a entrambi i membri, ottenendo:
107
Notiamo che
e
quadrato di binomio, aggiungiamo
: dunque per fare in modo che al primo membro si abbia un
ad ambo i membri:
ovvero:
Il secondo membro di quest'equazione è detto discriminante e in genere viene indicato con la lettera greca ∆
(Delta). Se
evidentemente non ci sono soluzioni reali, dal momento che il primo membro è
sempre maggiore o uguale a 0. In caso contrario, possiamo scrivere:
che con semplici passaggi possiamo riscrivere come:
Quest'ultima è nota come formula risolutiva delle equazioni di secondo grado.
EQUAZIONI TRINOMIE, in particolare BIQUADRATICHE
Le equazioni trinomie sono quelle riconducibili alla forma:
dove n è un intero positivo, a, b e c sono numeri reali (oppure complessi) e
. Posto:
possiamo riscrivere l'equazione in termini di y:
Risolvendo quest’equazione quadratica (detta equazione risolvente) e sostituendo nella relazione
precedente possiamo facilmente trovare le soluzioni cercate.
EQUAZIONI BINOMIE
Le equazioni binomie sono equazioni algebriche riconducibili alla forma:
axn + b = 0
dove n è un intero positivo, a e b sono numeri reali (o complessi e
dividendo per si ottiene:
. Portando
a secondo membro e
108
Nel caso di numeri reali, l'equazione può avere nessuna, una o due soluzioni. Se n è dispari, l'equazione
ammette l'unica soluzione
. Se n è pari, allora l'equazione è impossibile se
negativo; ammette le soluzioni
l'unica soluzione è x = 0
e
è un numero
in caso contrario. In particolare, se
,
EQUAZIONI DI GRADO SUPERIORE AL 2°
Per risolverle e necessario scomporle in fattori (applicando le regole della scomposizione dei polinomi) e
ricondursi al caso di equazioni di primo o secondo grado applicando la legge di annullamento del prodotto.
SISTEMI DI EQUAZIONI
Sono insiemi di due o più equazioni che devono essere soddisfatte dagli stessi valori attribuiti alle incognite.
La soluzione di un sistema e ogni soluzione comune a tutte le equazioni. I metodi di risoluzione più usati
sono: sostituzione, riduzione, confronto.
METODO DI SOSTITUZIONE
Si esplicita un'incognita esprimendola in funzione delle altre (per esempio y − 2x = − 3 diventa y = 2x − 3) in
una delle equazioni del sistema e si elimina l'espressione così ottenuta nelle altre equazioni in luogo
dell'incognita corrispondente. In questo modo l sparisce da tutte le equazioni eccetto la prima. Si applica
iterativamente il metodo fino a giungere ad una equazione con una sola incognita; si calcola il valore di
quest'ultima e si risale fino alla prima esplicitando via via i valori delle incognite calcolate.
Esempio:
Esplicitiamo z nella prima equazione e sostituiamolo dove compare nelle altre:
Ora calcoliamo x nella seconda in funzione di y:
In questo modo la terza equazione adesso contiene solo y: risolvendola viene
Quindi ora calcolando la x nella seconda viene la soluzione
109
METODO DI CONFRONTO
Si esplicita, in due delle equazioni, una delle variabili (o in generale, una stessa quantità), ottenendo così di
poter eguagliare i secondi membri (che risulteranno indipendenti dalla variabile esplicitata) per la proprietà
transitiva dell'uguaglianza. L'equazione così composta potrà essere riscritta al posto di una delle due
precedenti, ottenendo un sistema equivalente.
Esempio:
Isoliamo la variabile z nella prima e seconda equazione:
Confrontiamo le due espressioni risultanti:
Da cui risulta:
E risolvendo per sostituzione tra le prime due equazioni:
Dunque:
M ETODO DI RIDUZIONE
Si sostituisce una delle equazioni del sistema con una opportuna combinazione lineare di due equazioni del
sistema stesso, ottenendo un sistema equivalente a quello dato. Più precisamente, se due righe sono
espresse come prodotto tra opportune sottomatrici dei coefficienti ed il vettore x delle soluzioni, ovvero
110
allora è possibile sostituire una delle due con l'equazione
.
dove m e n sono due numeri scalari qualsiasi, entrambi diversi da zero.
Questo metodo è consigliato quando permette di trasformare il sistema dato in un altro più semplice, in cui
almeno una delle equazioni ha perso la dipendenza da qualche incognita.
Esempio:
Al posto della prima equazione scriviamo una combinazione lineare della prima e della seconda,
esattamente A + B, così da semplificare la variabile z:
Ora al posto della seconda equazione sostituiamo la combinazione lineare della prima e della seconda 3A −
4B, eliminando così la variabile y:
Così facendo abbiamo calcolato la x. Ora per semplice sostituzione completiamo la risoluzione del problema:
DISEQUAZIONI
una disequazione è una relazione di disuguaglianza tra due espressioni che contengono delle incognite. In
altri termini, dette
disequazione nelle variabili
,
, ...,
e
due funzioni definite in un insieme A, una
è un'espressione della forma:
oppure
111
Risolvere una disequazione significa trovare quell'insieme di valori che, attribuiti alle incognite, la rendono
una disuguaglianza effettivamente verificata. Solitamente, le soluzioni di una disequazione sono costituite da
uno o più intervalli di valori.
PRINCIPI DI EQUIVALENZA
Due disequazioni si dicono equivalenti se i rispettivi insiemi delle soluzioni coincidono. Vi sono due principi
che consentono di manipolare le disequazioni per trovare l'insieme delle soluzioni; essi sono una
conseguenza diretta delle proprietà delle disuguaglianze:
1. Principio di addizione: aggiungendo o sottraendo ai due membri di una disequazione una stessa
espressione, si ottiene una disequazione equivalente. Ciò implica che si può eliminare da entrambi i
membri uno stesso termine oppure spostarlo da un membro all'altro cambiandolo di segno (che
equivale ad aggiungere il suo opposto).
2. Principio di moltiplicazione: moltiplicando o dividendo i due membri di una disequazione per una
stessa espressione che sia sempre positiva si ottiene una disequazione equivalente alla data;
moltiplicando o dividendo per un'espressione negativa, la disequazione sarà controversa alla data.
Ciò implica che si può cambiare il segno a tutti i termini di entrambi i membri, purché si cambi anche
il verso della disequazione (in effetti, ciò equivale a moltiplicare per
).
una disequazione nelle incognite
grado quando è riconducibile alla forma:
(in generale numeri reali) si dice lineare o di primo
oppure
dove i coefficienti
possono essere interi, razionali o in generale reali.
DISEQUAZIONE LINEARE AD UN' UNICA INCOGNITA
È detta disequazione in un’incognita una disuguaglianza tra espressioni letterali verificata solo per particolari
valori attribuiti all’incognita. È detta soluzione di una disequazione ogni numero che, sostituito all’incognita,
verifica la disuguaglianza. Due disequazioni, nelle stesse incognite e aventi lo stesso dominio, sono dette
equivalenti quando tutte le soluzioni dell’una sono soluzioni dell’altra, e viceversa. Una disequazione lineare
ad una incognita si può sempre ricondurre ad una delle seguenti forme:
oppure
dove e sono numeri reali, con positivo. Ciò non costituisce una limitazione perché, se fosse negativo,
basterebbe cambiare il segno di entrambi i membri ed il verso della disequazione per ricondursi ad uno dei
due casi precedenti. Sottraendo ad entrambi i membri e dividendo per si vede facilmente che le due
disequazioni sono risolte, rispettivamente, da:
e
Una disequazione si dice quadratica se in essa, una volta ridotta in una delle forme seguenti, compaiono
termini quadratici, cioè potenze di ordine massimo uguale a 2.
Tutte le disequazioni quadratiche sono riconducibili, tramite le consuete semplificazioni a una forma del tipo:
112
•
•
•
•
con
. Se
si cambiano tutti i segni e il verso della disequazione.
Non è sufficiente che in una disequazione compaia un termine di secondo grado per affermare che essa è
quadratica: infatti la disequazione
termine di secondo grado si elide.
non è quadratica, in quanto il
A seconda che una disequazione abbia come segno il minore, maggiore, minore o uguale, maggiore o
uguale, ha un diverso metodo di risoluzione, che dipende anche dal discriminante dell'equazione associata.
L'equazione associata a una disequazione di 2º grado ha la stessa forma della disequazione, soltanto che
anziché il termine di disuguaglianza (
) compare il segno di uguaglianza.
Esempio: l'equazione associata alla disequazione
non è altro che l'equazione
.
Avendo introdotto l'equazione associata, è possibile calcolare il Delta (discriminante) dell'equazione (pari a
, ove è il coefficiente del termine di primo grado,
è il termine noto).
il coefficiente dell'incognita di secondo grado e
La risoluzione della disequazione passa attraverso lo studio del discriminante dell'equazione associata: ci
sono differenti metodi di risoluzione a seconda che esso sia positivo, negativo o nullo.
Se il discriminante è nullo, significa che l'equazione associata è riconducibile al quadrato di un binomio, in
quanto le soluzioni della equazione associata sono due e coincidenti:
riconduce quindi in una delle seguenti forme:
. La disequazione si
•
•
•
•
con
, quindi trascurabile. Per ognuno dei seguenti casi è sufficiente fare un piccolo ragionamento.
•
Primo caso:
. La disequazione è evidentemente impossibile, perché un quadrato (nel
caso in esame
•
Secondo caso:
), non può mai essere negativo, ma è sempre positivo o nullo.
. Un quadrato non può mai essere negativo, tuttavia può essere
nullo quando la base del quadrato si annulla. La base del quadrato si annulla se
se
, cioè
. Tutte le disequazioni con il segno minore o uguale hanno allora come risultato
, con
i coefficienti della x di secondo e primo grado nell'equazione associata.
113
•
Terzo caso:
. Un quadrato è sempre positivo, tranne quando la sua base si annulla.
Per far sì che la disequazione sia verificata, bisogna quindi escludere i valori per cui la base si
annulla: le soluzioni sono quindi tutte le
•
Quarto caso:
.
.
Un quadrato è sempre positivo o nullo, quindi la disequazione è verificata per ogni
.
ELEMENTI DI GEOMETRIA PIANA
ANGOLI
Si definisce angolo ciascuna delle due parti di piano individuate da due semirette uscenti dallo stesso punto.
Due angoli si dicono supplementari se la loro unione e un angolo piatto. Due angoli si dicono
complementari se la loro unione è un angolo retto.
ELEMENTI DI GEOMETRIA EUCLIDEA
TRIANGOLI
Si dice triangolo scaleno un triangolo con tre lati e tre angoli diversi tra loro.
Si dice triangolo isoscele un triangolo con due lati e due angoli uguali.
Si dice triangolo equilatero un triangolo con tre lati e tre angoli uguali.
Si dice triangolo rettangolo un triangolo con un angolo di 90°.
CRITERIO GENERALE DI UGUAGLIANZA TRA DUE TRIANGOLI RETTANGOLI
Se due triangoli rettangoli hanno ordinatamente uguali due elementi (che non siano i due angoli acuti), allora
essi sono uguali.
TEOREMA DEL TRIANGOLO ISOSCELE
In un triangolo isoscele l’altezza, la mediana, e la bisettrice relative alla base coincidono.
PUNTI NOTEVOLI DI UN TRIANGOLO
L’ortocentro e il punto d’intersezione delle altezze, esso può essere interno o esterno al triangolo, oppure
coincidente con uno dei suoi vertici.
Il baricentro e il punto d’intersezione delle mediane, esso e sempre interno al triangolo.
Il circocentro e il punto di intersezione degli assi dei lati del triangolo, esso e anche il centro della
circonferenza circoscritta al triangolo e può essere interno al triangolo, esterno o giacente su uno dei suoi
lati.
L’incentro e il punto d’intersezione delle bisettrici degli angoli del triangolo, esso e anche il centro della
circonferenza inscritta nel triangolo, ed e sempre interno al triangolo.
CRITERI DI CONGRUENZA DEI TRIANGOLI
Due triangoli sono congruenti tra loro se hanno congruenti due lati e l’angolo compreso.
Due triangoli sono congruenti se hanno congruenti due angoli e il lato ad essi comune.
114
Due triangoli sono congruenti se hanno congruenti due angoli e il lato opposto a uno di essi.
Due triangoli sono congruenti se hanno i tre lati rispettivamente congruenti.
10.5 PERIMETRO E AREA
Il perimetro di un triangolo e dato dalla somma dei suoi tre lati.
L’area del triangolo e data dal semiprodotto di base ed altezza del triangolo.
POLIGONI REGOLARI
Un poligono regolare ha tutti i lati e tutti gli angoli uguali, ed e inscrivibile e circoscrivibile in/ad una
circonferenza. Queste due circonferenze hanno lo stesso centro che viene definito centro del poligono.
Numero di
lati,
angoli e
vertici
Poligono
3
4
Angolo
interno
Perimetro
Triangolo
equilatero
60°
P= 3·b
Quadrato
90°
Disegno
Area
Gli angoli opposti sono congruenti, vale a
dire hanno uguale ampiezza: quindi
4
Rombo
.
Due angoli consecutivi sono supplementari,
con somma quindi pari a 180°:
α + β = 180°
4
Rettangolo
90°
P= 2·b+2·a
α + δ = 180°
4
Parallelogrammo
Trapezio
β + γ = 180°
P=a+b+c+d
115
CIRCONFERENZA E CERCHIO
La circonferenza e il luogo geometrico dei punti equidistanti da un punto fisso detto centro.
d = 2r
P = 2πr
A =πr2
Angoli alla circonferenza
Angoli alla circonferenza che insistono sullo stesso arco o su archi congruenti sono congruenti.
Angoli alla circonferenza che insistono su una semicirconferenza sono retti.
GEOMETRIA ANALITICA
COORDINATE SULLA RETTA
Definiamo ascissa di un punto P , su una retta orientata, sulla quale sia fissato un punto O come origine, la
misura del segmento OP , rispetto ad un’unita di misura (u ) precedentemente fissata.
DISTANZA TRA DUE PUNTI
La distanza orientata tra due punti di una retta, sulla quale e fissato un sistema di ascisse, e uguale alla
differenza tra l’ascissa del secondo punto e quella del primo.
PUNTO MEDIO DI UN SEGMENTO
L’ascissa del punto medio di un segmento e uguale alla semisomma delle ascisse degli estremi del
segmento stesso.
COORDINATE DEL PIANO
Fissati nel piano due assi mutuamente ortogonali, detti assi cartesiani, intersecantisi in O (origine), e scelti
come unita di misura due segmenti sovrapponibili per i due assi, è sempre possibile stabilire una
corrispondenza biunivoca e completa tra i punti P del piano e le coppie ordinate x (ascissa) e y (ordinata) di
due numeri reali. Si dice ascissa di P la misura del segmento che esprime la distanza di P dall’asse delle
ordinate; definiamo ordinata di P la misura del segmento che esprime la distanza di P dall’asse delle
ascisse.
DISTANZA TRA DUE PUNTI
La distanza assoluta tra due punti in un piano, nel quale e fissato un sistema di coordinate cartesiane
ortogonali, e uguale alla radice quadrata della somma dei quadrati delle differenze tra le coordinate
omonime dei due punti stessi.
PUNTO MEDIO
Le coordinate del punto medio di un segmento sono uguali alle semisomme delle coordinate omologhe degli
estremi del segmento stesso.
116
FUNZIONI
Due quantità variabili, che chiameremo genericamente x e y, sono l’una univocamente dipendente dall’altra,
quando ad ogni valore assegnato alla prima corrisponde uno ed un solo valore della seconda. La legge che
permette di passare da ogni x€X al corrispondente valore y€Y si dice anche funzione e si scrive:
y = f(x) (si legge “y è funzione di x”)
CAMPO DI ESISTENZA O DOMINIO DI UNA FUNZIONE
Il campo di esistenza (C.E.) o dominio della funzione e l’insieme X dei valori reali che si possono attribuire
alla variabile x , detta variabile indipendente, affinché esista il corrispondente valore reale delle y.
TIPI DI FUNZIONI
Suriettiva: ogni elemento b di B ha almeno una contro immagine a in A
Iniettiva: se ad elementi diversi dell’insieme A corrispondono immagini diverse in B
FUNZIONI DI PRIMO GRADO: LA RETTA
Definizione:
La retta è il luogo geometrico dei punti del piano le cui coordinate soddisfano un’equazione lineare in x e y
dalla forma: ax +by + c = 0 (equazione implicita della retta). Se b ≠ 0 ricaviamo l’equazione esplicita y = mx
+ q , dove m e il coefficiente angolare, ed indica l’inclinazione della retta rispetto all’asse delle x ; q e il
termine noto, e rappresenta l’ordinata del punto di intersezione della retta con l’asse y
Retta parallela all’asse delle x E` il luogo di punti aventi tutti la medesima ordinata:
y=K
Retta parallela all’asse delle y E` il luogo dei punti aventi tutti la stessa ascissa:
x=K
Retta passante per l’origine degli assi E` il luogo dei punti del piano per i quali e costante il rapporto tra
ordinata e ascissa.
Coordinate del punto d’intersezione tra due rette
Ricercare il punto d’intersezione di due rette, di equazioni rispettivamente ax +by + c = 0 e a' x + b' y + c'= 0 ,
significa trovare il punto le cui coordinate soddisfano entrambe le equazioni. La determinazione di tali
coordinate verrà quindi effettuata mediante la risoluzione del sistema:
a' x +b' y+ c'= 0
ax+ by+ c = 0 .
FUNZIONI QUADRATICHE: LA CIRCONFERENZA
La circonferenza è il luogo geometrico [ insieme di tutti e soli i punti che godono di una stessa proprietà]
dei punti del piano equidistanti da un punto fisso, detto centro.
Detto P(x,y) un generico punto del piano e `C(alpha,beta)` il centro della circonferenza di raggio r, in base
alla definizione data deve aversi:
117
`(x- alpha )^2+(y- beta)^2=r^2`
da cui, sviluppando i quadrati, si ottiene:
`x^2+y^2-2 alpha x-2 beta y+alpha^2+beta^2 - r^2=0`
Ponendo
`-2
alpha=a
`x^2+y^2+ax+by+c=0`(2)
-2beta=b
alpha^2+beta^2-r^2=c`,
l'equazione
assume
la
forma
che è l'equazione canonica o normale della circonferenza e che rappresenta un'equazione algebrica di
secondo grado nelle variabili x ed y.
FUNZIONI QUADRATICHE: LA PARABOLA
Parabola come luogo: dati una retta d ed un punto F, luogo dei punti P che hanno ugual distanza da F e da
d. Se scelgo bene il sistema di riferimento mi viene proprio (provare, è facile!) l’equazione della funzione di
secondo grado, con a = 1/2p, essendo p la distanza di F da d, oppure la forma canonica per i testi di
geometria y2= 2 p x. Dalla definizione geometrica si ricava:
la simmetria della curva rispetto alla perpendicolare per F a d (asse della parabola) (non è conseguenza
della scelta del riferimento…)
si può costruire la curva per punti: per ogni punto H su d, trovo un punto del luogo facendo l’intersezione
della perpendicolare a d in H con l’asse del segmento FH
sull’asse del segmento FH non ci sono altri punti della parabola oltre al punto P che sta sulla
perpendicolare a d: se P’ appartiene all’asse, P’F = P’H; se K è la proiezione ortogonale di P’ su d, la misura
di P’K è la distanza di P’ da d, ma essendo P’H l’ipotenusa di un triangolo rettangolo, è P’H = PF > P’K e
quindi P’ non appartiene alla parabola.
Definiamo punti interni alla parabola i punti del piano per cui la distanza dal fuoco è minore di quella dalla
direttrice, esterni i punti per cui la distanza dal fuoco è maggiore di quella dalla direttrice; il ragionamento
precedente mostra che per ogni punto H della direttrice, l’asse del segmento FH ha un solo punto comune
con la parabola e tutti gli altri esterni ad essa: chiamiamolo tangente alla parabola
Ne segue un modo di costruire con la piegatura della carta la parabola come inviluppo delle tangenti
(provare! Si segna un punto su un foglio di carta e si piega il foglio in modo di far passare un lato del foglio,
meglio il più lungo, per il punto, ripetendo varie volte la piegatura).
Ne segue anche la “proprietà focale” su cui si basano gli specchi e i fari parabolici: un raggio di luce
parallelo all’asse viene riflesso dallo specchio parabolico in un raggio che passa per il fuoco
118
(nel punto in cui il raggio incide lo specchio, questo è approssimato dalla retta tangente)
Tornando alla forma “comoda”
y = a x2 osserviamo: poiché a = 1/2p, il segno di a indica se la parabola sta nell’uno o nell’altro dei semipiani
individuati dall’asse delle x.
Se spostiamo l’origine degli assi, prendendo come nuova origine il punto (x0,y0), in modo che sia x’ = x − x0,
y’ = y − y0, dall’equazione “comoda” otteniamo la y '+ y0 = a(x '+ x0 )² .
Nel nuovo riferimento non sono cambiate le direzioni dell’asse della parabola e della sua direttrice; ne
deduciamo che una parabola con asse parallelo all’asse delle y (grafico di una funzione di secondo grado)
ha una equazione del tipo y = Ax² + Bx +C .
Possiamo confrontare le due ultime equazioni per ricavare le coordinate del vertice della parabola
determinata da y = Ax² + Bx +C .
Usiamo la tecnica del “completamento dei quadrati” per riscriverla nella forma
Y= A (x + B )² - B²+ C
2A
4A
ed ottenere che il vertice ha coordinate
−(B , - B²+4AC)
(2A
4A
)
La ricerca dei punti comuni alla parabola e all’asse delle ascisse coincide con la soluzione
dell’equazione di secondo grado Ax² + Bx +C = 0 .
Se A > 0 e 4AC − B2 > 0 (ovvero B2− 4 AC < 0) il vertice sta sopra l’asse delle x, quindi non ci sono
intersezioni….
Poiché le intersezioni l’asse della parabola è asse di simmetria, le intersezioni con una retta perpendicolare
all’asse di simmetria, in particolare le intersezioni con l’asse delle x, sono tali che il loro punto medio sta
sull’asse di simmetria, quindi le loro ascisse hanno come semisomma l’ascissa del vertice: in altre parole, se
α, β sono le radici dell’equazione Ax2 + Bx +C = 0 , allora α +β = −B/A.
Risolvere una disequazione di secondo grado Ax2 + Bx +C > 0 equivale a individuare i punti di ordinata
positiva della parabola di equazione y = Ax² + Bx +C ; ad esempio, se A < 0, ci sono punti a ordinata positiva
se e solo se il vertice ha ordinata positiva, etc….
119
FUNZIONI QUADRATICHE: L’ELLISSE E L’IPERBOLE
Ellisse:
Si dice ellisse il luogo di punti del piano per i quali e costante la somma delle distanze da due punti fissi, detti
fuochi. ’equazione canonica (o normale) dell’ellisse, cioè quella riferita a due assi di riferimento che
corrispondono ai suoi assi di simmetria, è la seguente:
x² + y² = 1
a²
b²
I punti in cui l’ellisse interseca gli assi di riferimento, detti vertici, sono V1 (a;0), V2 (a;0), V3 (0;b), V4 (0;-b)
Iperbole:
L’iperbole e il luogo dei punti del piano per i quali e costante, e diversa da zero, il valore assoluto della
differenza delle distanze da due punti fissi detti fuochi (F1 e F2 ). L’equazione dell’iperbole rispetto ad un
sistema di riferimento cartesiano ortogonale i cui assi x e y siano rispettivamente la retta dei fuochi e la retta
ad essa perpendicolare nel punto medio del segmento F1F2 e la seguente:
x² + y² = 1
a²
b²
L’iperbole interseca l’asse delle x in due punti, chiamati vertici reali dell’iperbole, le cui coordinate sono
V1(a;0) e V2 (a;0) . Gli asintoti hanno rispettivamente equazioni
y=b x ey=-bx
a
a
ESPONENZIALI E LOGARITMI
Esponenziali:
Se a e un numero positivo diverso da 1 ed x una variabile reale, posto y = ax si ottiene una funzione detta
esponenziale. Questa funzione assume valori positivi per qualunque valore attribuito all’esponente e non si
annulla mai; passa sempre per il punto P(0;1); per a > 1 la funzione e crescente, mentre per 0 < a <1 la
funzione e decrescente.
Logaritmi:
Se a e un numero positivo diverso da 1 l’espressione loga x (con x > 0 ) varia al variare di x ; posto y = loga x
si ottiene una funzione che viene detta logaritmica.
Per a > 1 la funzione logaritmica è: crescente
positiva per x >1
negativa per 0 < x <1;
Per 0 < a <1 la funzione e: decrescente
positiva per 0 < x <1
negativa per x> 1
120
TRIGONOMETRIA
Il piccolo diagramma sotto mostra una circonferenza con raggio pari a 1, chiamata circonferenza
trigonometrica. La linea grigia rappresenta un angolo a (inizia alla destra della linea rossa e gira in senso
orario). I valori della funzione seno (sin(a)) sono letti dalla linea verde (proiezione del punto di intersezione tra
la linea grigia e il cerchio trigonometrico). I valori della funzione coseno (cos(a)) sono letti dalla linea rossa (lo
stesso tipo di proiezione della funzione seno). I valori della funzione tangente (tan(a)) sono letti dalla linea blu
(punto d’intersezione tra il prolungamento della linea grigia e la linea blu.
TRIGONOMETRIA
SENI, COSENI, TANGENTI E COTANGENTI DI ANGOLI NOTI
La trigonometria (dal greco trígonon (τρίγωνον, triangolo) e métron (µέτρον, misura): risoluzione del
triangolo) è la parte della matematica che studia i triangoli a partire dai loro angoli. Il compito principale della
trigonometria, così come rivela l'etimologia del nome, consiste nel calcolare le misure che caratterizzano gli
elementi di un triangolo (lati, angoli, mediane, etc.) partendo da altre misure già note (almeno tre, di cui
almeno una lunghezza), per mezzo di speciali funzioni. Tale compito è indicato come risoluzione del
triangolo. Tra i possibili sistemi di misura degli angoli e degli archi, quelli più usati sono il sessagesimale,
che utilizza come unita il grado (novantesima parte dell’angolo retto), e quello in radianti, la cui unita di
misura e il radiante (secondo tale sistema l’angolo al centro in una circonferenza e dato dal rapporto tra
l’arco sotteso ed il raggio).
Le misure di uno stesso angolo nei due sistemi sono collegate dalla relazione di conversione:
α°: α r = 180° :π
RELAZIONI TRA LE FUNZIONI TRIGONOMETRICHE DI UNO STESSO ANGOLO
Dall’applicazione del teorema di Pitagora: (senx)² + (cos x)² =1
tgx= senx
cos x
FORMULE DI ADDIZIONE E SOTTRAZIONE
In trigonometria, le formule di addizione e sottrazione permettono di trasformare le funzioni
trigonometriche della somma o differenza di due angoli in un'espressione composta da funzioni
trigonometriche dei due angoli.
FORMULE DI ADDIZIONE[MODIFICA]
•
•
121
•
•
FORMULE DI SOTTRAZIONE[MODIFICA]
•
•
•
•
ANGOLI NOTI
Gradi
Radianti
sen α
cos α
tan α
tg α
0°
0
0
1
0
30°
Π
1
√3
√3
6
2
2
3
Π
√2
√2
1
1
4
2
2
Π
√3
1
√3
√3
3
2
2
3
Π
1
0
0
2π
√3
-1
3
2
2
3π
√2
- √2
4
2
2
180°
π
0
-1
270°
3π
-1
0
0
1
45°
60°
90°
√3
2
120°
135°
-√3
- √3
3
-1
-1
0
2
360°
2π
0
122
FORMULE PARAMETRICHE
Queste formule saranno tra quelle più usate: serviranno soprattutto per risolvere equazioni trigonometriche
di primo grado
Servono ad esprimere le funzioni seno e coseno mediante la tangente dell'angolo metà [siccome tang(x/2)
sarà di solito indicata con t verranno indicate come formule parametriche (t parametro) ]
2t
sen α =
---------1+t
2
2
1-t
cos α =
---------1+t
2
2t
tang α =
---------2
1-t
RISOLUZIONE DEI TRIANGOLI
Detti A,B,C i lati di un triangolo generico e gli angoli opposti a ognuno di essi, si può scrivere:
RISOLUZIONE DI UN TRIANGOLO RETTANGOLO ( C = ipotenusa):
B = C senβ
B = A tgβ
RISOLUZIONE DI UN TRIANGOLO QUALSIASI:
Teorema del coseno: A2 =B2 + C2 - 2BC cosα
Teorema dei seni: A = B = C
Senα senβ senγ
AREA DI UN TRIANGOLO:
Noti due lati, ad esempio B e C , e l’angolo compreso α :
S = 1 · B · C · sen α
S = superficie
2
Area di un triangolo isoscele essendo noti L (uno dei due lati uguali) e l’angolo al vertice α:
S= L2 ·sen (α) · cos(α)
(2)
(2)
EQUAZIONI E DISEQUAZIONI TRIGONOMETRICHE
EQUAZIONI TRIGONOMETRICHE ELEMENTARI
Un'equazione trigonometrica o goniometrica è un'equazione in cui l'incognita compare come argomento
di una o più funzioni trigonometriche, quali seno, coseno e tangente.
Ad esempio, un'equazione trigonometrica è:
123
o anche:
Invece, un'equazione del tipo:
non è un'equazione trigonometrica, poiché l'incognita x non compare come argomento di alcuna funzione
trigonometrica. Le equazioni trigonometriche più semplici sono quelle riconducibili alle forme seguenti:
Le equazioni (1) e (2) sono evidentemente impossibili se | a | > 1.
EQUAZIONE IN CUI COMPARE SOLO UNA FUNZIONE TRIGONOMETRICA
Le equazioni in cui figura una sola funzione trigonometrica (dello stesso argomento) si possono ricondurre
immediatamente alle equazioni elementari, prendendo tale funzione come incognita ausiliaria. Ad esempio:
Posto sinx = y, si ottiene l'equazione algebrica nell'incognita y:
che ha le soluzioni y = 1 e y = 1 / 2. È quindi sufficiente risolvere le equazioni elementari sinx = 1 e sinx = 1 / 2,
le cui soluzioni sono rispettivamente da
e
.
EQUAZIONE IN CUI COMPAIONO PIU FUNZIONI TRIGONOMETRICHE
Qualora compaiano più funzioni trigonometriche (dello stesso argomento), si possono in generale esprimere
tutte le funzioni trigonometriche per mezzo di una sola tramite le note identità trigonometriche, per poi
proseguire come nell'esempio precedente:
In questo caso è conveniente usare sostituire sin2x = 1 − cos2x, ottenendo, dopo pochi calcoli, l'equazione:
EQUAZIONI LINEARI IN SENO E COSENO
Sono equazioni del tipo asinx + bcosx = c , con a, b, c numeri reali assegnati, che supporremo diversi da
zero (infatti nel caso in cui a o b fossero uguali a zero si avrebbe di nuovo un'equazione elementare, il caso
in cui c sia uguale a zero verrà esaminato più avanti).Per risolvere questo tipo di equazioni conviene
124
sostituire sinx e cosx con le loro corrispondenti espressioni razionali in funzione di tg(x/2) valide, come si è
visto in precedenza per x p + 2kp, si avrà quindi:
svolgendo i calcoli si otterrà l'equazione di secondo grado in tg(x/2):
2
(b + c)(tg(x/2)) - 2atg(x/2) + c - b = 0
se questa avrà due soluzioni reali, le chiameremo r1 e r2 , si avranno le seguenti equazioni elementari, di cui
si conosce la soluzione: tg(x/2) = r1
tg(x/2) = r2
Per l'equazione lineare data potrebbero essere però soluzioni anche i valori del tipo x = p + 2kp, che non si
possono avere col metodo descritto a causa delle restrizioni imposte dalle formule usate; se però si verifica il
caso in cui b + c = 0 , si ha un'equazione di primo grado intera intg(x/2) al posto della (1) di cui x = p + 2kp
sono soluzioni.
DISEQUAZIONI TRIGONOMETRICHE
Molte disequazioni trigonometriche si possono risolvere per via grafica, cioè analizzando o i grafici delle
funzioni trigonometriche, o il cerchio goniometrico.
Es. senx>½ π < x < 5 π
6
6
STATISTICA E CALCOLO DELLE PROBABILITA`
CALCOLO COMBINATORIO
Serve a determinare il numero dei diversi tipi di raggruppamenti (a gruppi di k elementi) che si possono
formare con n elementi.
DISPOSIZIONI SEMPLICI
Con disposizioni di n oggetti a k a k (Dn,k) si definisce numero di modi in cui e possibile disporre n oggetti
presi k alla volta (a k a k), ove ciascuna disposizione differisce dalle altre o per gli oggetti o per il loro
ordine.
PERMUTAZIONI
Una permutazione di un insieme di oggetti è una presentazione ordinata, cioè una sequenza, dei suoi
elementi nella quale ogni oggetto viene presentato una ed una sola volta. Per contare quante siano le
permutazioni di un insieme con n oggetti, si osservi che il primo elemento della configurazione può essere
scelto in n modi diversi, il secondo in (n-1), il terzo in (n-2) e così via sino all'ultimo che potrà essere preso in
un solo modo essendo l'ultimo rimasto. Dunque, indicando con Pn il numero delle possibili permutazioni di un
insieme di n elementi, si ottiene che esse sono esattamente n! (n fattoriale):
125
Ad esempio le permutazioni degli elementi dell'insieme {a,b,c} sono 3! = 6: abc, bac ,bca, cab, cba, acb. Un
altro esempio può essere il seguente: In quanti modi possibili possiamo anagrammare la parola -ATRIO-,
contando anche le parole prive di significato: ATRIO n=5; P5= 5 * 4 * 3 * 2 * 1 = 120 modi di anagrammare la
parola ATRIO. N.B: nella parola ATRIO nessuna lettera si ripete.
Per completare meglio la definizione di fattoriale fissiamo anche i valori seguenti:
1! = 1 e 0! = 1.
COMBINAZIONI
Si chiama combinazione semplice una presentazione di elementi di un insieme nella quale non ha
importanza l'ordine dei componenti e non si può ripetere lo stesso elemento più volte. La collezione delle
combinazioni di k elementi estratti da un insieme S di n oggetti distinti si può considerare ottenuta dalla
collezione delle disposizioni semplici di lunghezza k degli elementi di S ripartendo tali sequenze nelle classi
delle sequenze che presentano lo stesso sottoinsieme di S e scegliendo una sola sequenza da ciascuna di
queste classi. Ciascuna delle suddette classi di sequenza di lunghezza k contiene k! sequenze, in quanto
accanto a una sequenza σ si hanno tutte e sole quelle ottenibili permutando i componenti della σ. Quindi il
numero delle combinazioni semplici di n elementi di lunghezza k si ottiene dividendo per k! il numero delle
disposizioni semplici di n elementi di lunghezza k:
Di solito tra le diverse disposizioni semplici di una classe si sceglie come combinazione rappresentativa la
sequenza nella quale i componenti compaiono in ordine crescente (tutti gli insiemi finiti possono avere gli
elementi ordinati totalmente, ovvero associati biunivocamente ai primi interi positivi).
CALCOLO DELLE PROBABILITA`
Si chiama probabilità P di un evento aleatorio E, previsto da una determinata prova, il quoziente fra il
numero dei risultati favorevoli e il numero dei risultati possibili della prova, nell’ipotesi che siano tutti
egualmente possibili.
P (E) = casi favorevoli
casi possibili
Proprietà
la probabilità e quindi un numero sempre compreso tra 0 e 1 (perche il numeratore è sempre minore o al
massimo uguale al denominatore)
quando P(E) = 0 l’evento E è impossibile
quando P(E) = 1 l’evento E è certo
due eventi E ed F si dicono opposti quando il non verificarsi di E implica il verificarsi di F; l’evento opposto
di E viene anche detto complementare e si indica E
Siano E ed F due eventi incompatibili; la probabilità che si verifichi E oppure F e uguale alla somma delle
probabilità dei singoli eventi
Attenzione: due eventi si dicono incompatibili quando non possono accadere contemporaneamente
Siano E ed F due eventi indipendenti; la probabilità che si verifichino contemporaneamente e data dal
prodotto delle probabilità dei singoli eventi
126
Attenzione: due eventi si dicono indipendenti se il realizzarsi di uno non implica il realizzarsi del secondo
MEDIA ARITMETICA
La media aritmetica è il tipo di media impiegato più comunemente e quello al quale, con il termine "media", si
fa in genere riferimento nel parlare comune. Viene usata per riassumere con un solo numero un insieme di
dati su un fenomeno misurabile (per esempio, l'altezza media di una popolazione). Viene calcolata
sommando i diversi valori a disposizione, i quali vengono divisi per il loro numero complessivo.
La formula della media aritmetica semplice per n elementi è:
MEDIA PONDERATA
La media aritmetica ponderata (o media pesata) è una combinazione lineare convessa dei dati in analisi.
Ciascun valore è moltiplicato per il proprio peso. La formula generale è:
dove f rappresenta il peso di ciascun termine.
127
Le informazioni contenute nel presente volume sono state estrapolate da:
Wikipedia
Disegno dell’Architettura - Prof. Arch. Alessandro Merlo
www.sapere.it
Lezioni di fisica, meccanica e termodinamica del Prof. Tullio Papa
Politest “Comprensione verbale”
“Teoritest” Hoepli “
“Dispensa corso di preparazione architettura” Lista aperta
“English” Test Alphatest
www.testdilogica.it (Pierpaolo Caserta)
Scultura contemporanea (Articolo di Laura Panarese)
AA. VV., L’Universale Architettura, Garzanti Libri, Milano 2004
AA. VV., Storia dell’Arte, Istituto Geografico De Agostini, Novara 1976
ADORNO P., L’arte italiana, Volume primo Tomo primo, Edizioni G. D’Anna, Firenze 1994
BOSSAGLIA R., Dizionario di terminologia di storia dell’arte, Edizioni Bignami, Milano 1995
DE FUSCO R., Il codice dell’architettura, Liguori Editore, Napoli 2003
DIDEROT, D’ALAMBERT, L’Encyclopédie, Volume Architettura, Libritalia, 2000
LUCIE-SMITH E., Dizionario dei termini d’arte, Franco Muzio Editore, Padova 1988
MORASSO E., Manuale di disegno, Electa Mondadori, Milano 1991
MOROLLI G., Le membra degli ornamenti, Alinea Editrice, Firenze 1986
L’assonometria Marco Cardini
128












