Mario Gilli
LEZIONE 12
Massimizzazione dei profitti in concorrenza perfetta
Massimizzazione dei profitti in generale
1
2
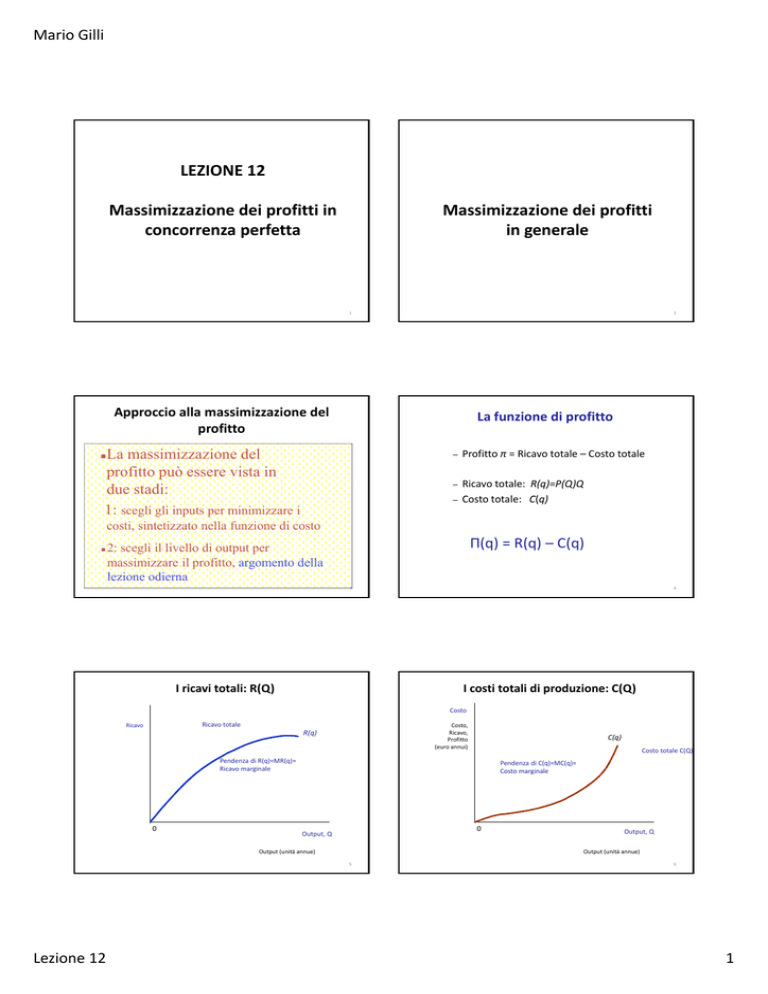
Approccio alla massimizzazione del profitto
La funzione di profitto
La massimizzazione del
profitto può essere vista in
due stadi:
1: scegli gli inputs per minimizzare i
–
Profitto π = Ricavo totale – Costo totale
–
Ricavo totale: R(q)=P(Q)Q
C t t t l C( )
Costo totale: C(q)
–
costi, sintetizzato nella funzione di costo
Π(q) = R(q) – C(q)
2: scegli il livello di output per
massimizzare il profitto, argomento della
lezione odierna
3
I ricavi totali: R(Q)
4
I costi totali di produzione: C(Q)
Costo
Ricavo totale
Ricavo
Costo,
Ricavo,
Profitto
(euro annui)
R(q)
C(q)
Costo totale C(Q)
Pendenza di R(q)=MR(q)= Ricavo marginale
0
Pendenza di C(q)=MC(q)= Costo marginale
0
Output, Q
Output (unità annue)
Output (unità annue)
5
Lezione 12
Output, Q
6
1
Mario Gilli
La massimizzazione del profitto
Il grafico della funzione di profitto
•Per massimizzare il profitto:
Costo,
Ricavo,
Profitto
(euro annui)
• occorre trovare il livello di produzione che rende massima la differenza fra ricavi e costi
i i
ti
R(Q)
• Confrontando R(q) e C(q), il massimo profitto si ha quando
Q=50
R(q)
A
7500
C(Q)
•Il grafico della funzione di profitto è tracciato come differenza tra la curva di R(Q) e C(Q).
Costo,
Ricavo,
Profitto
(euro annui)
R(Q)
5000
5000
2500
R(q)
A
7500
C(Q)
5000
2500
0
q0
π (q )
0
Q
50
q0
50
Q
Slide 7
Slide 8
Ricavo marginale, costo marginale e massimizzazione del profitto
Il ricavo marginale e il prezzo
• Un aumento della quantità venduta (ΔQ) modifica il ricavo dell’impresa in due modi:
• L’impresa vende ΔQ unità addizionali di output, ognuna delle quali ad un prezzo pari a P(Q) • effetto di espansione del prodotto
• Per poter vendere le unità aggiuntive, l
Per poter vendere le unità aggiuntive l’impresa
impresa deve deve
abbassare il prezzo praticato: il ricavo si riduce sulle (Q‐ ΔQ) unità originarie
• effetto di riduzione del prezzo
• Le imprese price‐taker fronteggiano una curva di domanda perfettamente orizzontale, per cui non sono soggette all’effetto di riduzione del prezzo
• Il ricavo marginale è il reddito addizionale
che deriva dalla produzione di una unità
aggiuntiva di output.
MR =
ΔR
R (Q ) − R (Q − Δ Q )
=
ΔQ
ΔQ
• Il costo marginale è il costo aggiuntivo
derivante dalla produzione di una unità
addizionale di output.
MC =
ΔC (Q ) C (Q ) − C (Q − ΔQ )
=
ΔQ
ΔQ
9
10
Ricavo marginale, costo marginale e massimizzazione del profitto
Il ricavo marginale e il prezzo
Curva discendente della domanda
Curva orizzontale domanda (Impresa taker)
•
della Price‐
• Confrontando R(q) e C(q)
•R(q) > C(q)
•R’ > C’
•
Effetto di Espansione del Effetto
di Espansione del
prodotto
P
Effetto di riduzione del prezzo D
P(Q−ΔQ)
Effetto di Espansione del prodotto
ΔP < 0
P
•Indica p
profitti p
più
(Q )
alti p
per Costo,
Ricavo,
Profitto
R(q)
output maggiori
•Il profitto è crescente
C
C(q)R(q)
A
B
D
π (q )
Q − ΔQ
ΔQ > 0
Lezione 12
Q
0
Q − ΔQ
Q
ΔQ > 0
Output 11
π (q )
0
q*
q0
Output 12
2
Mario Gilli
Ricavo marginale, costo marginale e massimizzazione del profitto
Ricavo marginale, costo marginale e massimizzazione del profitto
•
• Confrontando R(q) e C(q)
–Livelli di output oltre q*: •R(q)> C(q)
•C’ > R’
Costo,
Ricavo,
Profitto
A
R(q)
•Il profitto è decrescente
C
C(q)R(q)
•Il profitto è massimo
quando:
Costo,
Ricavo,
Profitto
R(q)
•R’(Q)=C’(Q)
B
C
C(q)R(q)
A
B
π (q )
0
q*
q0
Output π (q )
0
q*
q0
13
14
Ricavo marginale, costo marginale e massimizzazione del profitto
Ricavo marginale, costo marginale e massimizzazione del profitto
Π = R ‐ C
Output C’ = ΔC/Δq
Il profitto è massimo quando
Π’ = R’ – C’ = 0, cioè il costo marginale
è uguale al ricavo marginale:
R’ = ΔR/Δq
Π’ = ΔΠ/Δq = R’ – C’
= ΔR/Δq ‐ ΔC/Δq
R’(q) = C’ (q)
15
16
Il volume di vendite che massimizza il profitto
• Per individuare la quantità di vendite che massimizza Π:
• Passaggio 1: Regola della quantità (Condizione di ottimo)
• Calcolare il livello di Q tale che
• MR MR = MC
MC
• Se vi sono più livelli di Q che soddisfano tale condizione, scegliere il livello di Q associato al Π più alto
• Passaggio 2: Regola di chiusura (Condizione di break even)
• Verificare se i Π associati alla Q calcolata nel passaggio 1 sono maggiori ai Π associati a Q=0
17
Lezione 12
LA CONCORRENZA
PERFETTA
&
Le imprese price‐takers
18
3
Mario Gilli
• Offerta ottimale per un'impresa in concorrenza perfetta (1)
• Un’impresa produce un unico bene con costo totale CT(x).
• Questo bene è una commodity. Esiste pertanto un prezzo di mercato per il bene: • qualsiasi produttore o venditore cerchi di vendere a un prezzo superiore rimane senza clienti, mentre qualsiasi impresa venda a un prezzo pari o anche leggermente d
h l
inferiore ottiene tutti i clienti che desidera. • Indichiamo con p il prezzo di mercato del bene. • Ipotizziamo che l’impresa consideri il prezzo p come dato; nella terminologia economica un’impresa di questo tipo è price taker ossia concorrenziale
• Offerta ottimale per un'impresa in concorrenza perfetta (2)
• La condizione di accettare il prezzo come dato è un’astrazione effettuata nei modelli e non una verità assoluta. Tale condizione è approssimativamente soddisfatta in alcune situazioni, per le quali speriamo e, sulla base dei dati empirici ci aspettiamo che i modelli
sulla base dei dati empirici, ci aspettiamo che i modelli teorici forniscano informazioni e previsioni utili. • Esistono settori che, anche in termini approssimativi, soddisfano le ipotesi della concorrenza perfetta? – I prodotti agricoli
– le risorse naturali
– lo spazio per uffici nel centro di una grande area metropolitana
19
Le imprese price‐takers
L’IMPRESA CHE NON FA IL PREZZO
• Un’impresa si dice price‐taker quando:
• può vendere una qualsiasi quantità al prezzo P • non vende nulla per prezzi maggiori di P • LL’impresa
impresa price taker
price taker fronteggia una curva di fronteggia una curva di
domanda perfettamente orizzontale
• L’impresa price taker ha un potere di mercato nullo
21
Le decisioni di offerta
delle imprese price takers
• Le imprese price takers scelgono la quantità Q di output che massimizza il profitto secondo due regole:
• PASSAGGIO 1
• Regola della quantità (Condizione di ottimo)
• Nel caso generale:
g
• MR=MC
• Per l’impresa price‐taker: • MR = P
• La regola della quantità diventa:
• P=MC
23
Lezione 12
20
Un’impresa che non fa il prezzo decide come agire con la
consapevolezza di non poter influire sui prezzi dei prodotti che
vende o dei fattori che acquista.
La curva di domanda della singola impresa indica la quantità
del prodotto dell’impresa che viene domandata per ogni prezzo
praticato da q
p
quell’impresa.
p
p
D( p )
p
x
NB: Un’impresa che non
fa il prezzo si trova di
fronte a una curva di
domanda che è
infinitamente elastica in
corrispondenza del prezzo
di mercato
22
• La funzione di offerta di un’impresa price taker, parte prima:
• la funzione di offerta “è” (all’incirca) la funzione del costo marginale
• Se l’impresa considera p come dato, quale quantità produce o offre al mercato come funzione di p? • Questa quantità, considerata come funzione o(p) del prezzo p, è la funzione di offerta dell’impresa.
• Iniziamo con un’impresa che non sostiene costi fissi, ossia CT(0) = 0, ed è soggetta a un costo marginale crescente:
• o(p) è definito da CMa[o(p)] = p
24
4
Mario Gilli
ANALISI GEOMETRICA (1)
• Per qualsiasi prezzo p sull’asse verticale, la quantità che l’impresa fornisce è il livello x cui corrisponde questo costo marginale
• CMa(x) e o(p) non sono affatto la stessa funzione. • CMa fornisce un valore in termini monetari come CM f i
l
i t
i i
t i
funzione della quantità, mentre
• la funzione di offerta fornisce il valore della quantità del bene come funzione del prezzo • Una funzione è l’inverso dell’altra. Decisione di offerta di un’impresa price taker: la regola della quantità
Prezzo
($ per
unità)
MC
Regola della quantità
P
MR=P (=Funzione
di Domanda inversa)
Output
Q*
25
26
Costi marginali
Costi
Curva d’offerta
MC(x)
P
x
o(p)
x
27
ANALISI GEOMETRICA (2)
• Perché prima abbiamo scritto che la funzione di offerta “è” (all’incirca) la funzione del costo marginale? • Perché il segmento lungo l’asse verticale costituisce parte della funzione di offerta mentre
costituisce parte della funzione di offerta, mentre non appartiene alla funzione del costo marginale: – per prezzi inferiori al costo marginale minimo, l’uguaglianza p = CMa(x) non può essere risolta e l’impresa non offre alcuna quantità
29
Lezione 12
28
• La funzione di offerta di un’impresa price taker, parte seconda: (1)
• un costo marginale crescente e un costo fisso positivo
• Ipotizziamo che queste condizioni portino alla funzione di costo medio usuale a forma di U
• Non cambia nulla per i prezzi inferiori al costo p
p
marginale minimo (l’impresa offre una quantità nulla) • né per i prezzi superiori al costo medio minimo, dove l’offerta dell’impresa scorre lungo la funzione del costo marginale
30
5
Mario Gilli
Le decisioni di offerta delle imprese price takers
• La funzione di offerta di un’impresa price taker, parte seconda: (2)
• Ma, indicando con p** il costo marginale minimo e con p* il costo medio minimo, questo caso è più complesso per i prezzi compresi tra p* e p**.
• Questa complessità dipende dall’eventuale capacità dell’impresa
dell
impresa di evitare il costo fisso producendo una di evitare il costo fisso producendo una
quantità nulla.
• Se il costo fisso non è evitabile, allora è irrilevante per le decisioni di offerta dell’impresa. L’offerta dell’impresa è quindi esattamente come prima
• Se, invece, l’impresa evita il costo fisso producendo una quantità nulla, allora, per i prezzi inferiori a p* l’impresa non produce
• PASSAGGIO 2
• Regola di chiusura:
• Confrontare il Π quando l’impresa produce q
p
p
Q* e quando produce zero.
• Scegliere il livello di produzione associato ai Π più alti
• Che cosa significa questa regola?
31
La regola di chiusura in assenza di costi non recuperabili
32
Decisione di offerta di un’impresa price taker: la regola della quantità+ la regola di chiusura
Prezzo
($ per
unità)
• In assenza di costi non recuperabili:
• Π=0 se Q=0
• Quindi
• Π(Q*)=PQ‐C(Q*)>0 • Se
• P > C(Q*)/Q* = AC(Q*)
• Il prezzo è maggiore del costo medio in corrispondenza di Q*
MC
Profitto
AC
P
MR=P (=Funzione
di Domanda inversa)
AC(Q*)
ACmin
Qe
Q*
33
Cosa succede se il prezzo è basso...
P
MC
Cosa succede alla quantità ottima quando il Per un dato P troviamo il Q ottimo
Facciamo diminuire i prezzi... prezzo diminuisce...
MC
AC
P
P
P
P
P
PP
P
x
prezzo <
Costo medio
x
35
Lezione 12
34
AC
P
x* = 0
Output
x x xxx
36
6
Mario Gilli
La regola di chiusura in assenza di costi non recuperabili
Curva di offerta
Dall’analisi del grafico:
• Acmin è il costo medio associato alla scala efficiente di produzione (quando AC=MC)
• La regola di chiusura si semplifica e diventa:
• se P > Acmin: Π è massimo in corrispondenza di una quantità pari a Q*
• se P < Acmin: Π è massimo in corrispondenza di una quantità pari a Q=0
• se P = Acmin: l’impresa è indifferente fra chiudere e produrre la quantità ottima (Π = 0 in ogni caso)
x=o(p)
Output multiplo
a questo prezzo
P
_
x
Per nessun prezzo si produce in questo spazio
37
38
La funzione di offerta di un’impresa price‐taker
La funzione di offerta di un’impresa price‐taker
• La funzione di offerta individuale di un’impresa mostra la quantità che l’impresa ritiene ottimale produrre per ogni possibile livello del prezzo: • Qs = S(P)
( )
• Per derivare la funzione di offerta di un’impresa, occorre applicare:
9 la regola di quantità (condizione di ottimo)
9la regola di chiusura
• Per P>ACmin, la quantità di vendite che massimizza il profitto per l’impresa è positiva e soddisfa la regola di quantità (condizione di ottimo)
– Qs soddisfa P = MC
• Per P=ACmin, l’impresa è indifferente fra l’ipotesi di chiudere la produzione e quella di produrre secondo la sua scala di produzione efficiente
• Per P<ACmin, l’impresa non produce:
– Qs=0
39
La curva di offerta di un’impresa price‐taker
40
• COSTI MARGINALI COSTANTI
Costi
MC
AC
P’
AC
P’
CMa
ACmin
ACmin
x
Qe=0
Lezione 12
S(P’)
Qe S(P’)
41
42
7
Mario Gilli
• La funzione di offerta di un’impresa price taker, parte terza: (2)
La funzione di offerta con CMa costante
p
Se il prezzo è superiore al CMa costante, l’offerta è infinita
• Il comportamento estremo che descrive questa funzione d’offerta è il risultato di un’applicazione troppo rigorosa del modello: Se il prezzo è uguale al CMa costante, ll’offerta
offerta è pari a qualsiasi quantità, perché è pari a qualsiasi quantità perché
il profitto è sempre zero
– il costo marginale non può essere costante per il
i l
ò
sempre e, anche se lo fosse, l’impresa capirebbe che alla fine, per qualche scala di produzione, i prezzi si ridurrebbero
CMa
Se il prezzo è inferiore al CMa costante, l’offerta è nulla, altrimenti il profitto è negativo
x
43
44
Variazioni nel prezzo degli input sulla funzione di offerta
La legge dell’offerta
Legge dell’offerta
se P aumenta L’output ottimale (che max Π) di un’impresa price‐taker è non‐
i f i
inferiore al livello l li ll
ottimale di output prima dell’aumento di prezzo
La curva di offerta individuale è non‐
decrescente
• Come si modifica la funzione di offerta di un’impresa quanto cambia il prezzo di un input?
• Un incremento di prezzo di un input comporta un aumento del costo unitario di produzione
Ricavo, costo
9 Le curve AC e MC si spostano verso l’alto
C
R=P°Q
9 La curva di offerta si trasla anch’essa verso l’alto
• Un incremento nei costi fissi:
9 Fa spostare verso l’alto la curva AC verso l’alto
Q* Output
9 Lascia invariate la curva MC
46
46
Variazioni nel prezzo degli input sulla funzione di offerta Variazioni nel prezzo degli input sulla funzione di offerta •Aumento del costo variabile
•Aumento del costo fisso evitabile
•Aumento del costo variabile
MC2
MC2
MC1
MC1
10
5
Qe
Qe
47
Lezione 12
48
8
Mario Gilli
Offerta di lungo periodo e di breve periodo
La regola di quantità
• AC e MC di un’impresa possono essere diversi nel breve e nel lungo periodo. • Equilibrio di breve e di lungo periodo non coincidono
• Se il prezzo dell’output aumenta improvvisamente: S il
d ll’ t t
t i
i
t
cosa succede all’equilibrio?
• Usare le regole di quantità e di chiusura per analizzare gli effetti di breve e di lungo periodo di un incremento di prezzo sull’output dell’impresa
Supponiamo un aumento del prezzo da P° a P^
La quantità ottima di vendite per l’impresa è:
MCBP
MCLP
–Q*BP nel breve periodo
–Q
Q*LP nel lungo periodo
nel lungo periodo
Nel lungo periodo, la quantità ottima
aumenta
P^
P°
Q* QBP* QLP*
51
49
Il surplus del produttore
La regola di chiusura
P^ è superiore al costo medio evitabile di breve periodo in corrispondenza di Q*BP ed è superiore a quello P^
di lungo periodo in corrispondenza di Q*LR
CMBP
CMLP
ACBP
ACLP
P°
Le imprese decideranno di produrre •nel breve periodo
•nel lungo periodo • L’impresa guadagna una rendita su tutte le unità vendute, tranne l’ultima
• La rendita o surplus del produttore è la somma, su tutte le unità prodotte, della
differenza tra prezzo e costo
e costo marginale.
• Profitto = Rendita del produttore ‐ Costi non recuperabili
Q* Q*BP Q*LP
52
52
Rendita del produttore
Prezzo
($ per
unità di
output)
In q* C’ = R’.
Tra 0 e q* , R’ > C’ per tutte le unità.
Rendita del
produttore
C’
CMV
B
A
D
0
P
C
q*
Alternativamente, il costo
variabile complessivo è la
area del rettangolo ODCq* .
Il ricavo è l’area OABq*.
Il surplus del produttore è
l’area di ABCD.
Output
53
Lezione 12
Le funzioni di domanda e offerta aggregata 54
9
Mario Gilli
• Le funzioni di domanda e offerta aggregata
• Abbiamo bisogno di aggregare le funzioni di domanda e di offerta perché tutta la nostra analisi di comportamento è a livello individuale ma i mercati operano a livello aggregato
ma i mercati operano a livello aggregato
• Aggregare significa semplicemente sommare. • Ricordiamo in primo luogo come si aggregano le curve di domanda
• La funzione di domanda aggregata (1)
• Tutta la domanda proviene da consumatori in concorrenza perfetta • La curva di domanda del mercato è data da:
D( p ) = d1 ( p ) + ... + d M ( p )
• Se tracciate il grafico della domanda totale, ricordate che il prezzo è Se t acc ate g a co de a do a da tota e, co date c e p e o è
posto sull’asse verticale, pertanto dovete sommare le funzioni in senso orizzontale
• Supponete che vi vengano date le funzioni di domanda inverse per tre individui
• Per trovare la domanda inversa totale, dovete sommate queste tre funzioni? No!
• Per trovare la domanda inversa aggregata dovete invertire le funzioni di domanda inversa. 55
• La forma della curva di domanda aggregata può essere differente dalla forma delle curve di domanda individuali: in questo esempio le curve di domanda individuali sono lineari, mentre la curva di domanda aggregata è lineare a tratti.
56
• La funzione di offerta aggregata (1)
• Ora, analogamente a quanto fatto per le curve di domanda, vediamo come passare dalle funzioni di offerta delle singole imprese a l
f i i di ff
funzioni di offerta aggregata. • Come è possibile aggregare le offerte delle singole imprese?
p
lezione 19
x
57
58
Costruiamo la curva di offerta del A P' l’impresa 1 entra nel mercato
Per prezzi minori di P' nessuna impresa Per prezzi maggiori di P" entrambe le Con prezzi compresi tra P' e
P" solo La curva di offerta dell’impresa 1 ...
A P" l’impresa
2 entra nel mercato
mercato...
imprese offrono
opera nel mercato
l’impresa 1 produce
P E la curva di offerta dell’impresa 2 ...
P
P
• La funzione di offerta aggregata (2)
• Tutta l’offerta proviene da imprese concorrenziali. • La curva di offerta di tutto il settore è data da:
O( p) = o1 ( p) + ... + oN ( p )
• L’offerta totale per ogni prezzo è esattamente la somma orizzontale delle offerte delle singole imprese per tale prezzo. • Perché orizzontale? • Perché poniamo sempre il prezzo sull’asse verticale, perciò – come nel caso delle domande – fissiamo il prezzo e sommiamo le quantità orizzontalmente 60
Lezione 12
P"
P'
x1
Impresa a
costi bassi
P"
x2
P'
Impresa a
costi alti
x1 +x2
Entrambe le
imprese
La curva di offerta aggregata
è la somma orizzontale delle
curve di offerta delle singole
60
imprese
10
Mario Gilli
• La funzione di offerta aggregata (4)
• Notate che la forma della curva di offerta aggregata può essere differente dalla forma delle curve di offerta individuali: • in questo esempio le curve individuali erano lineari ma la curva di offerta aggregata è lineare a tratti
61
Lezione 12
11












