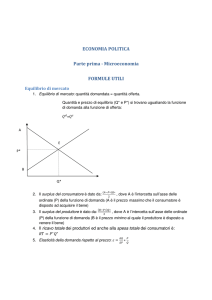
Principi di Economia - Microeconomia
Esercitazione 5
Monopolio
Soluzioni
Daria Vigani
Novembre 2014
1. Dite se le seguenti affermazioni sono vere o false e spiegate perché.
• In un settore caratterizzato da concorrenza perfetta la curva di domanda è orizzontale, mentre in monopolio è inclinata negativamente.
FALSO. In entrambi i casi, la curva di domanda ha pendenza negativa. Se consideriamo la singola impresa perfettamente concorrenziale,
la sua curva di domanda è orizzontale. Poiché la singola impresa è
troppo piccola per influenzare il mercato (price taker ), potrà vendere
qualunque unità desideri a quel prezzo.
• Le imprese perfettamente concorrenziali non sono in grado di controllare il prezzo di vendita del proprio prodotto. VERO. Se impongono
un prezzo più alto usciranno dal mercato; se impongono un prezzo
più basso, non massimizzeranno il profitto.
2. Se un monopolista potesse applicare la discriminazione di prezzo perfetta:
(a) la curva del ricavo marginale e la curva di domanda coinciderebbero;
(b) la curva del ricavo marginale e la curva del costo marginale coinciderebbero;
(c) ciascun consumatore pagherebbe un prezzo diverso;
(d) il ricavo marginale diventerebbe negativo ad un determinato livello
di output;
(e) il tipo di transazione che ne deriva continuerebbe ad essere socialmente inefficiente.
La risposta corretta è la A: il monopolista venderebbe ciascuna unità addizionale di prodotto esattamente al prezzo di riserva, generando quindi
un ricavo pari al prezzo di riserva. Domanda e ricavo marginale, dunque,
coincidono.
1
La risposta B è palesemente errata, cosı̀ come la risposta C, poichè è possibile che due o più consumatori abbiano lo stesso prezzo di riserva.
La risposta E è errata, dal momento che l’ultima unità di prodotto è venduta ad un prezzo che eguaglia il costo marginale (come in concorrenza
perfetta), l’esito sarebbe quindi socialmente efficiente.
3. Considerate un monopolista operante nel mercato di un particolare videogioco.
La curva di domanda di mercato è p(q) = 80 − 2q , la curva di costo
marginale è M C = q, e i costi fissi ammontano a 400 euro.
(a) Rappresentate graficamente la curva di domanda, la curva di costo
marginale e, dopo averla ricavata analiticamente, la curva del ricavo
marginale.
La funzione dei ricavi nel nostro caso sarà:
R(q) = p(q) · q = (80 − q/2) · q = 80q −
q2
2
La funzione di ricavo marginale non è altro che la derivata, rispetto
a q, della funzione dei ricavi. Quindi:
M R(q) = 80 − q
.
Grafico
p
MC
80
MR
D
q
160
(b) Calcolate e indicate nel grafico il prezzo e la quantità di equilibrio in
monopolio.
In monopolio, la condizione per la massimizzazione del profitto è che
2
i costi marginali siano uguali ai ricavi marginali. Dalla condizione
M R = M C ricaviamo la quantità di equilibrio in monopolio:
MR = MC
80 − q = q ⇒ 2q = 80 ⇒ q M = 40
A questo punto, sostituiamo la quantità di equilibrio nella funzione
di domanda, per ottenere il prezzo di monopolio:
pM = 80 −
qM
= 80 − 20 = 60
2
p
MC
pM = 60
40
D
q
M
q
= 40
(c) Qual è il profitto del monopolista?
Il profitto realizzato sarà pari al totale dei ricavi meno il totale dei
costi. Dal momento che nei nostri dati non ci sono informazioni
riguardo la funzione dei costi, per calcolare il profitto del monopolista
possiamo utilizzare la seguente formula:
π = (pM − M C) · q M − F C
dove tutte le variabili saranno calcolate nel punto di equilibrio e F C
sono i costi fissi.
Dunque avremo
π = (60 − 40) · 40 − 400 = 400
(d) Qual è il surplus dei consumatori?
Il surplus del consumatore è identificato dall’area sottostante la curva di domanda, al di sopra del prezzo di equilibrio, e rappresenta la
differenza tra il prezzo che i consumatori sono disposti a pagare per
un determinato bene e il prezzo di mercato.
3
p
MC
pM = 60
40
D
q
M
q
= 40
Nel nostro caso il surplus sarà dato dall’area gialla nel grafico
CS = (40 · 20)/2 = 400
(e) Quali sarebbero il prezzo e la quantità di equilibrio se ci trovassimo in
un mercato perfettamente concorrenziale? In concorrenza perfetta,
gli imprenditori sono costretti a vendere al costo marginale: abbiamo
cioè p = M C. Mettendo questa condizione a sistema con la domanda,
otteniamo
160
80 − q/2 = q =⇒ q ∗ =
≈ 53, 3
| {z } |{z}
3
p(q)
MC
e quindi p∗ = 80 − q/2 ≈ 53, 3.
Quindi,
• il prezzo si abbassa (pM = 60 > p∗ = 53),
• la quantità venduta aumenta (q M = 40 < q ∗ = 53),
4