Il concetto di limite in Matematica - TED

Limite infinito
Si parla di limite infinito di una funzione nei casi in cui il valore di una funzione
cresce sempre di più, tendendo quindi a più infinito.
Esempio:
1
lim
 
x  3  x  32
il limite per x che tende a 3
si legge
di
1
x  32
è uguale a  
Il significato dell’affermazione è che quanto più il valore di x si approssima a 3,
tanto più il valore della funzione aumenta, tendendo quindi a + infinito.
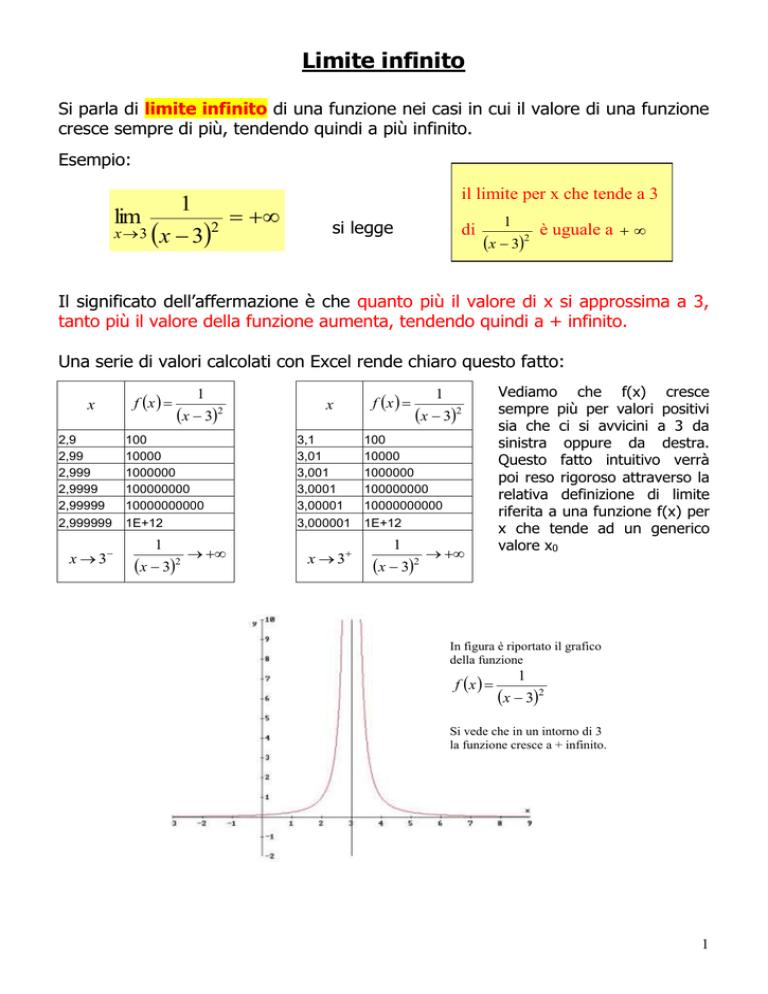
Una serie di valori calcolati con Excel rende chiaro questo fatto:
x
2,9
2,99
2,999
2,9999
2,99999
2,999999
x  3
f x  
1
x  3
2
100
10000
1000000
100000000
10000000000
1E+12
1
x  3
2
 
x
3,1
3,01
3,001
3,0001
3,00001
3,000001
x  3
f x  
1
x  3
2
100
10000
1000000
100000000
10000000000
1E+12
1
x  32
 
Vediamo che f(x) cresce
sempre più per valori positivi
sia che ci si avvicini a 3 da
sinistra oppure da destra.
Questo fatto intuitivo verrà
poi reso rigoroso attraverso la
relativa definizione di limite
riferita a una funzione f(x) per
x che tende ad un generico
valore x0
In figura è riportato il grafico
della funzione
f x  
1
x  32
Si vede che in un intorno di 3
la funzione cresce a + infinito.
1
DEFINIZIONE DI LIMITE + INFINITO
lim f  x   
Si dice che x  x
0
quando:
M  0  I x0  : x  I x0   x  x0

f x   M
traduzione:
Per ogni M > 0 (grande a piacere) esiste un intorno I di x 0 tale che “x
appartenente a tale intorno e x diverso da x0” implica che f(x) sia maggiore di M


Per quanto grande si possa scegliere Mnoi potremo sempre trovare un intorno di x0 che ha
questa proprietà: se x appartiene a quell’intorno allora f(x) è maggiore di M, non importa
quanto grande M sia.
Se sceglieremo M più grande allora gli intorni di x0 diventeranno più piccoli, ma esisteranno
sempre e per i valori x in tali intorni i valori f(x) della funzione saranno maggiori di qualsiasi M.
Il grafico nella pagina successiva chiarisce meglio questa argomentazione.
2
y

f(x)
 
y = f(x)
M
x0  1  x0
x x0   2
x
Nella figura è disegnato il grafico di una funzione per la quale
lim f  x   
x  x0
Il grafico si disegna coi seguenti criteri:
 Disegniamo, in rosso e un po’ a caso, una parte del grafico della funzione
 Dopo aver scelto M (grande a piacere) fissiamo sull’asse y il suo valore.
 Tracciamo una linea orizzontali fino a incontrare il grafico della funzione
 Dai punti di incontro tracciamo delle linee verticali fino a incontrare l’asse x
 I valori sull’asse x corrispondenti ci danno gli estremi
l’intorno I  x 0  cercato (in figura è disegnato in blu).
x 0   1 e x 0   2 che definiscono
 Prendiamo una x qualsiasi in quell’intorno e vediamo dal grafico che il valore f(x)
corrispondente è maggiore di M

Questo vale per ogni x appartenente all’intorno.
Se scegliessimo un altro M più grande potremmo ripetere lo stesso procedimento
grafico e troveremmo sull’asse x un intorno più piccolo, ma lo troveremmo sempre.
Abbiamo così rispettato il significato della definizione di limite e tale significato
comprende e completa in modo rigoroso la definizione “intuitiva” .
Armati della definizione rigorosa di limite proviamo ora a DIMOSTRARE che il limite
dell’esempio specifico fatto all’inizio ha proprio quel valore. Lo facciamo come esercizio nella
pagina successiva.
3
1
 
x  3  x  32
lim
Dimostrare, usando la definizione di limite, che
M  0  I x0  : x  I x0   x  x0

f x   M
 In questo caso partiremo dalla disequazione f x   M e la risolveremo cercando un intorno
di x0 in cui sia soddisfatta questa disequazione
Visto che x tende a 3 nel nostro caso cercheremo un intorno I(3)
 partiamo quindi da:
f x   M

1
x  32
M

1
x  32

M x  32
x  32
 Possiamo semplificare il denominatore, visto che è un quadrato e quindi positivo, mettendo
come condizione di esistenza x  3 e ottenendo:
1  M x  32
 1  Mx 2  6Mx  9M
 Mx 2  6Mx  9M  1  0
La disequazione è di 2° grado. Calcoliamo x1,2 usando la formula ridotta:
x1,2 
 3M  9 M 2  9 M 2  M  3M  M
M

 3 
M
M
M
Col metodo grafico della parabola troviamo come soluzione:
3
M
M
 x 3
M
M
Questo ci fornisce l’intorno:

M
M
 che è l’intorno di 3 che cercavamo.
I 3   3 
,3

M
M


Abbiamo quindi dimostrato che
M  0  I 3 : x  I 3  x  3 
ovverossia che
1
M
2
x  3
1
 
x  3  x  32
lim
Nella pagina a seguito diamo la definizione per il caso in cui il limite sia   . In tal caso la
funzione decresce per valori sempre più grandi tendendo a   quando x tende a x0.
La definizione è molto simile a quella che abbiamo visto poco fa, basta sostituire alla
condizione f x   M la condizione corrispondente f x    M
4
DEFINIZIONE DI LIMITE - INFINITO
lim f  x   
Si dice che x  x
0
quando:
M  0  I x0  : x  I x0   x  x0

f x    M
traduzione:
Per ogni M > 0 (grande a piacere) esiste un intorno I di x 0 tale che “x
appartenente a tale intorno e x diverso da x0” implica che f(x) sia minore di -M


Per quanto grande si possa scegliere Mnoi potremo sempre trovare un intorno di x0 che ha
questa proprietà: se x appartiene a quell’intorno allora f(x) è minore di -M, non importa
quanto grande M sia.
Se sceglieremo M più grande allora gli intorni di x0 diventeranno più piccoli, ma esisteranno
sempre e per i valori x in tali intorni i valori f(x) della funzione saranno maggiori di qualsiasi M.
In figura è riportato il grafico
della funzione
f x   
1
x  32
Si vede che in un intorno di 3 la
funzione decresce a - infinito.
Nei relativi esercizi di dimostrazione partiremo dalla disequazione f x   M e la risolveremo
cercando un intorno di x0 in cui sia soddisfatta questa disequazione.
5