1.3
L’effetto tunnel (trattazione semplificata)
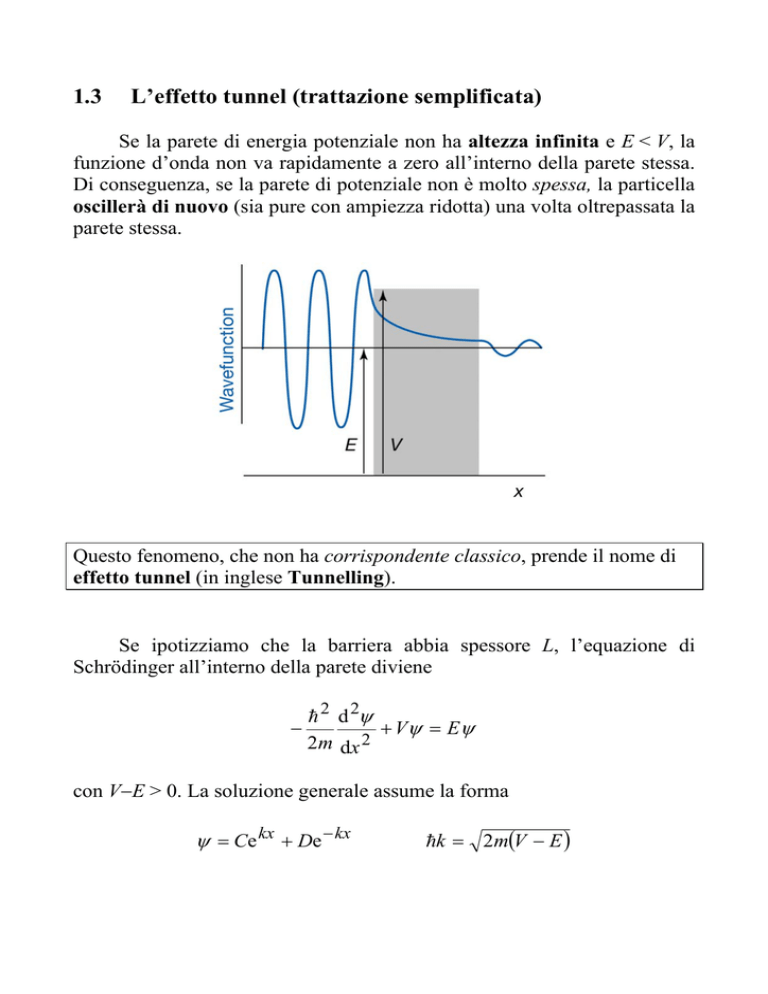
Se la parete di energia potenziale non ha altezza infinita e E < V, la
funzione d’onda non va rapidamente a zero all’interno della parete stessa.
Di conseguenza, se la parete di potenziale non è molto spessa, la particella
oscillerà di nuovo (sia pure con ampiezza ridotta) una volta oltrepassata la
parete stessa.
Questo fenomeno, che non ha corrispondente classico, prende il nome di
effetto tunnel (in inglese Tunnelling).
Se ipotizziamo che la barriera abbia spessore L, l’equazione di
Schrödinger all’interno della parete diviene
h 2 d 2ψ
−
+ Vψ = Eψ
2 m dx 2
con V−E > 0. La soluzione generale assume la forma
ψ = Ce kx + De − kx
hk = 2m(V − E )
Dal momento che l’ampiezza della funzione d’onda deve andare a
zero all’interno della parete di potenziale, deve essere C = 0. La funzione
d’onda decresce quindi esponenzialmente all’interno della parete.
La funzione d’onda complessiva consiste quindi 1) di un’onda
incidente, 2) di un’onda riflessa, 3) di un’ampiezza che decresce
esponenzialmente, 4) di un’onda che si propaga dopo la barriera:
La probabilità di trasmissione attraverso la barriera, T, è data dalla
relazione (non dimostrata)
−1
kL
− kL 2
e −e
con ε = E
T = 1 +
16ε (1 - ε )
V
(
L(2mV )1 / 2 / h
)
(1)
Per barriere di potenziale alte e larghe (kL >> 1), la relazione (1) si
riduce a
T = 16ε (1 − ε )e − 2kL
La probabilità di trasmissione decresce quindi esponenzialmente
(come atteso) con lo spessore della barriera e con m1/2.
2.
Il moto vibrazionale
Si dice che una particella esperimenta un moto armonico se è
sottoposta ad una forza del tipo F = − kx , dove k prende il nome di
costante di forza. Poiché F = −dV / dx , il potenziale corrispondente
assume la forma
V =
1 2
kx
2
(energia potenziale di tipo parabolico)
In questo caso, l’equazione di Schrödinger monodimensionale si scrive:
(− h2 / 2m)d 2ψ / dx 2 + 12 kx 2ψ = Eψ
(1)
Anche in questo caso la particella è costretta entro una buca di
potenziale simmetrica (=energia quantizzata). Differenze rispetto alla
buca di potenziale quadrata:
1. per spostamenti ampi l’ampiezza della funzione d’onda va a zero più
lentamente;
2. l’energia cinetica della particella dipende dallo spostamento in
maniera più complessa, poiché V=V(x).
2.1 La soluzione formale dell’equazione (cenni)
Con i cambi di variabile y = x/α e ε = E/(½ћω), dove α = ћ/(mk)½ e
ω = (k/m) ½, l’equazione (1) si semplifica nel seguente modo:
(
)
d 2ψ / dx 2 + ε − y 2 ψ = 0
(2)
Il passo successivo consiste nello studio dell’equazione per spostamenti
molto ampi. Si ha
d 2ψ / dx 2 − y 2ψ = 0
(3)
che presenta come soluzioni approssimate exp(y2/2) e exp(−y2/2). La
prima funzione è inaccettabile, in quanto tende all’infinito. La seconda,
invece, va a zero per x crescente ed è quindi compatibile con l’esistenza di
una parete di potenziale.
Possiamo quindi supporre che la funzione d’onda esatta sia della
forma ψ = f exp − y 2 / 2 , dove f simboleggia una funzione che non
aumenta più velocemente con x di quanto exp(−y2) diminuisca.
Introducendo questa soluzione di prova nell’equazione (2) si ha:
(
)
f "−2 yf '+ (ε − 1) f = 0
(4)
che prende il nome di equazione differenziale di Hermite (molto ben
studiata dai matematici). Le soluzioni accettabili della equazione (4)
esistono solo per ε = 2ν + 1, con ν = 0, 1, 2,…, n.
2.2 I livelli energetici
Ricordando che si era posto ε = E/(½ћω), si ottengono i livelli
energetici dell’oscillatore armonico
Eν = (ν + ½) ћω
con ν = 0, 1, 2,…, n
e
ω = (k/m) ½
Caratteristiche:
• l’intervallo tra i livelli vale ∆E = Eν +1 − Eν = ћω;
• esiste una energia di punto zero che vale E0 = ½ћω. La ragione
fisica di ciò risiede nel fatto che la particella è vincolata nella sua
buca di potenziale, perciò la sua posizione non è del tutto incerta e
per il principio di indeterminazione il suo momento non può essere
nullo.
• La particella oscilla attorno alla sua posizione di equilibrio.
Quanto vale ћω per un oggetto di dimensioni microscopiche? Si supponga
un legame chimico abbia costante di forza k = 500 Nm-1.
2.3 Le funzioni d’onda
Le funzioni d’onda sono determinate dalle soluzioni della equazione
di Hermite (polinomi di Hermite)
( )dyν exp(− y 2 )
dν
Hν ( y ) = (− 1)ν exp y
la funzione d’onda complessiva è data da
( )
ψν = Nν Hν ( y ) exp − y 2
con Nν2 =
1
απ
1/ 2 ν
fattore di normalizzazione e ν = 0, 1, 2, …, n.
2 ν!
I polinomi di Hermite in funzione di ν valgono:
ν
0
1
2
3
...
Hν(y)
1
2y
4y2−2
8y3−12y
...
Distribuzioni di probabilità per alcuni stati dell’oscillatore armonico. Per
valori crescenti di ν le regioni di massima probabilità si muovono verso i
punti di inversione (minima velocità per l’oscillatore classico).
3.
Il moto rotazionale
Data una particella puntiforme di massa m in moto su una
circonferenza di raggio r, si definisce momento di inerzia, I, la quantità
I = mr2
Il moto rotazionale è descritto dal momento angolare, J, che è
l’equivalente del momento lineare nel moto traslazionale
J = Iω
3.1 Il moto in due dimensioni: la particella su un anello
Consideriamo una particella vincolata a muoversi sulla circonferenza
di raggio r nel piano x,y. Il suo momento angolare lungo l’asse z, Jz, vale
in modulo |Jz |= |pr |= |mvr|. L’energia vale
J z2
J z2
p2
E=
=
=
2m 2mr 2 2 I
3.1.1 Discussione qualitativa della quantizzazione del momento angolare
Considerando che Jz = ±pr, dalla relazione di de Broglie otteniamo
Jz = ±
hr
λ
dove i segni opposti corrispondono a opposti versi di rotazione.
Supponiamo che λ possa assumere valori arbitrari: in questo caso,
la funzione d’onda sarà in generale polidroma. Questo è incompatibile
con le richieste fatte sulla forma delle soluzioni delle equazioni agli
autovalori. Soluzioni accettabili esistono solo per certi valori di λ e, di
conseguenza, per determinati valori del momento angolare e
dell’energia.
L’energia della particella è quantizzata.
In particolare, le sole lunghezze d’onda ammesse (tali da rendere la
funzione monodroma) sono:
λ=
2πr
ml
dove ml, chiamato numero quantico di momento angolare, è un intero
≥ 0. Il momento angolare è allora limitato ai valori
Jz = ±
hr
λ
=
ml hr ml h
=
= ml h
2πr
2π
con ml = 0, ±1, ±2, …
Valori positivi e negativi di ml corrispondono a rotazioni in senso orario e
antiorario, rispettivamente.
L’energia del moto rotazionale è limitata ai
valori
2 2
J z2 ml h
E=
=
2I
2I
e le corrispondenti funzioni
normalizzate assumono la forma
ψ ml (φ ) =
d’onda
e iml φ
(2π )1 / 2
N.B. Questi risultati sono stati raggiunti con considerazioni di tipo
“classico” e usando solo la relazione di de Broglie. Devono essere
controllati risolvendo esplicitamente l’equazione di Schrödinger.
L’energia è funzione del quadrato di ml, quindi è indipendente
(come atteso) dal senso di rotazione. Gli stati sono doppiamente degeneri
(tranne quello con ml = 0).
Valori crescenti del momento angolare corrispondono a un
crescente numero di nodi della funzione d’onda.
Proviamo a localizzare la particella attraverso la densità di probabilità
e iml φ
*
ψ ml ψ ml =
(2π )1 / 2
*
e iml φ e − iml φ e iml φ 1
=
=
(2π )1 / 2 (2π )1 / 2 (2π )1 / 2 2π
che è indipendente da φ. Quindi la posizione della particella è
completamente indefinita.
Angolo e momento angolare sono osservabili complementari.
3.1.2 Costruzione dell’operatore quantistico momento angolare
Classicamente il vettore momento angolare è dato dal prodotto vettoriale
i
L = r× p = x
px
j
y
py
k
z = i yp z − zp y + j ( zp x − xp z ) + k xp y − yp x
p z
(
)
(
)
per cui la componente z vale
(
l z = xp y − yp x
)
Con le regole viste al capitolo precedente, otteniamo per l’operatore
quantistico in coordinate cartesiane l’espressione
lz =
h ∂
∂
x − y
i ∂y
∂x
che in coordinate polari diviene (notare l’indipendenza da r)
lz =
h ∂
i ∂φ
Con l’operatore così costruito possiamo verificare la correttezza
della funzione d’onda proposta (a meno della costante di normalizzazione)
l zψ ml =
h ∂ψ ml
h
= iml e iml φ = ml hψ ml
i ∂φ
i
ψ ml è una autofunzione di lz e ammette come autovalore il momento
angolare ml h .
3.2 Il moto in tre dimensioni: la particella su una sfera
Consideriamo una particella di massa m libera di muoversi sulla
superficie di una sfera (caso importante per lo studio degli elettroni
nell’atomo e delle molecole rotanti).
Abbiamo bisogno di una coordinata aggiuntiva: la particella deve
soddisfare a due condizioni al contorno
⇓
Il momento angolare è caratterizzato da due numeri quantici
L’angolo θ prende il nome di colatitudine, mentre φ è l’angolo azimutale.
3.2.1 L’equazione di Schrödinger (cenni)
Poiché la particella è vincolata a muoversi su di una superficie, la
coordinata r è costante e si ha V=0 (superficie equipotenziale).
L’equazione da risolvere è allora
h2 2
−
∇ ψ (θ , ϕ ) = Eψ (θ ,ϕ )
2m
La soluzione di questa equazione mostra che le funzioni d’onda accettabili
sono specificate da sue numeri quantici
(numero quantico di momento angolare orbitale)
(numero quantico magnetico, 2l + 1 valori)
l = 0, 1, 2, …
ml = l, l−1,…, −l
Le funzioni d’onda si indicano con Yl , ml (θ ,φ ) e prendono il nome di
armoniche sferiche.
l
ml
Yl , ml (θ ,φ )
1/ 2
0
0
1
4π
1/ 2
1
0
3
4π
1/ 2
1
±1
…
…
3
8π
cosθ
e ± iφ sin θ
…
L’energia delle particelle è ristretta ai valori
h2
E = l (l + 1)
2I
ed è indipendente da ml. Di conseguenza, uno stato caratterizzato da
numero quantico l è (2l + 1) volte degenere.
Rappresentazione grafica delle funzioni d’onda
3.2.2 Il momento angolare e la quantizzazione spaziale
Nella visione classica, l’energia di una particella è legata al
momento angolare dalla relazione E = J 2 / 2 I . Confrontando questa
espressione con la relazione ottenuta risolvendo l’equazione di
Schrödinger si osserva che
L = [l (l + 1)]1 / 2 h
l = 0, 1, 2, …
l z = ml h
ml = l, l−1,…, −l
Se il momento angolare è rappresentato da un vettore di lunghezza
[l (l + 1)]1 / 2 in unità h , per rappresentare correttamente il valore della
componente z il vettore deve essere orientato in modo tale che la sua
proiezione sull’asse z valga ml.
L’orientazione di un corpo rotante rispetto all’asse di un campo
elettromagnetico esterno è quantizzata.
La quantizzazione spaziale fu mostrata per la prima volta da Stern e
Gerlach nel 1921 (prima ancora della formulazione della meccanica
quantistica), facendo passare un fascio di atomi di argento in un campo
magnetico fortemente disomogeneo.
(risultato classico)
(risultato quantistico)
Poiché l’operatore lˆz commuta con L̂ ma non con lˆx e lˆy , il modo
più corretto di rappresentare la quantizzazione spaziale è dato dal
cosiddetto modello vettore
4.
Lo spin (cenni)
Stern e Gerlach osservarono solo due bande nel loro esperimento.
Questo sembrava in conflitto con i risultati quantistici che prevedevano
l’osservazione di 2l + 1 orientazioni per ogni valore di l, che è uguale a 2
solo per l = ½.
Il conflitto fu risolto suggerendo che il momento angolare da essi
osservato non fosse dovuto al moto orbitale dell’elettrone attorno al
nucleo, ma al moto dell’elettrone attorno al suo asse. Questo momento
angolare intrinseco è chiamato spin.
E’ quindi necessario introdurre altri due numeri quantici (Dirac,
seconda quantizzazione) che prendono il nome di numero quantico di
spin, s, e numero quantico magnetico di spin, ms.
S = [s(s + 1)]1 / 2 h
s z = ms h
ms = s, s−1,…, −s
Per l’elettrone si ha s=1/2