probabilità che il lettore n. 1 non venga utilizzato sarebbe dunque

34
Capitolo 2 Modelli discreti
probabilità che il lettore n. 1 non venga utilizzato sarebbe dunque stata
(^Vl-l^OJS?.
\0)\0 /
I due risultati sono molto vicini. Era forse da prevedere?
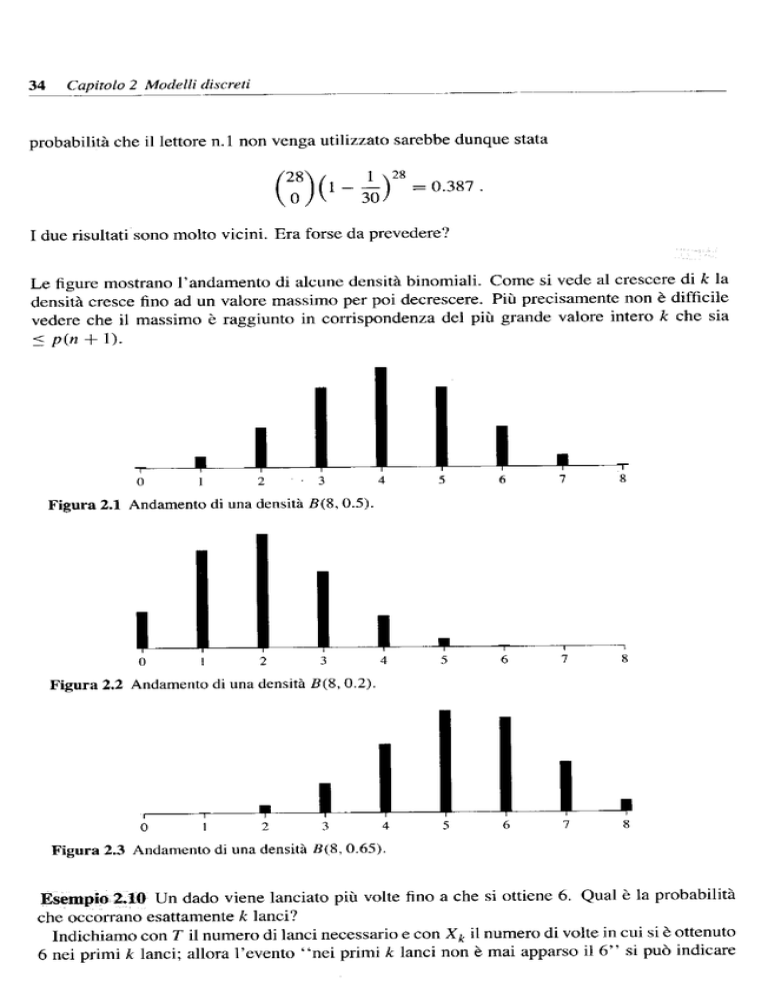
Le figure mostrano l'andamento di alcune densità binomiali. Come si vede al crescere di k la
densità cresce fino ad un valore massimo per poi decrescere. Più precisamente non è difficile
vedere che il massimo è raggiunto in corrispondenza del più grande valore intero k che sia
< p(n + 1).
O
1
2
• • 3
I
4
Figura 2.1 Andamento di una densità B(8,0.5).
I
0
1
2
3
4
Figura 2.2 Andamento di una densità B(8, 0.2).
0
1
2
3
4
5
6
7
8
Figura 2.3 Andamento di una densità S(8, 0.65).
Esempio 2.10 Un dado viene lanciato più volte fino a che si ottiene 6. Qual è la probabilità
che occorrano esattamente k lanci?
Indichiamo con T il numero di lanci necessario e con Xk il numero di volte in cui si è ottenuto
6 nei primi k lanci; allora l'evento "nei primi k lanci non è mai apparso il 6" si può indicare
2.2 Variabili aleatorie discrete e loro distribuzioni
35
Somme geometriche
I calcoli di quantità relative alla distribuzione geometrica richiedono una certa dimestichezza
con le somme geometriche, di cui è opportuno richiamare alcune proprietà. La relazione
chiave è, per x / 1 ,
-xn+l
1 —x
1 + x + . . . + xn =
(2.7)
Questa si verifica immediatamente moltiplicando il denominatore di destra per il termine di
sinistra e osservando che tutti i termini si elidono, tranne il primo e l'ultimo. Dalla (2.7) si
ricava subito, per \ \ 1 , il valore della somma della serie
,2.8,
f>' _
Da queste relazioni se ne possono ricavare altre per derivazione: poiché la (2.8) vale per
ogni x | < 1, derivando a destra ed a sinistra rispetto a x e ricordando (o dando per scontato)
che in una serie di potenze si può derivare termine a termine all'interno dell'intervallo di
convergenza, si ottiene
oo
T—\
co
oo
n=0
n=\é
T—\
x—^
oo
„
T—\
.
cc
1
oo
1
> (n + l)x" =^>» A
nx" T
+^
> Ax" = ^n
> nx"
^«-TI,A
A +
T-j—^
n=0
n=0
n=0
n=0
Quindi troviamo la relazione
oo
(2.9)
Ynx
(I-*) 2
1-*
O-*) 2
indifferentemente con {T > k] oppure con {A^ — 0}; poiché sappiamo che Xk segue una legge
B(k, p) con p = g, abbiamo
P(T > k) = P(Xk = 0) =
Ma chiaramente si ha {T = k} U {T > k} = {T > k — 1} e l'unione è disgiunta. Dunque
= /t) =P(7 > J t - l ) - P ( r > fc)e,perit= 1,2, . . . ,
(2.10)
P(T =k) = (l- p ) k ~ ] - (1 - P)k = p(\
36
Capitolo 2 Modelli discreti
Definizione 2.11 Si chiama densità geometrica di parametro p (O < p < I) la densità
(2.11)
O
altrimenti .
Si chiama geometrica modificata di parametro p la densità definita da
(2-12)
_
P)*"1 k = ì,2,...
altrimenti.
= IP
„
IO
I calcoli dell'Esempio 2.10 indicano che il tempo di primo successo della successione di lanci
in uno schema successo-insuccesso segue una legge geometrica modificata.
La (2.3) è facilmente verificata per la densità geometrica ricordando il valore della somma di
una serie geometrica
^(1
k__
1
_ I
E facile anche vedere che, se una v.a. Z segue una legge geometrica modificata, allora Z — 1
segue una legge geometrica. Infatti, per k = O, 1 , . . . ,
P(Z - 1 = k) = P(Z = k + 1) = p(\ p)k.
Osservazione 2.12 Nell'Esempio 2.10 siamo stati un po' sbrigativi: abbiamo definito una v.a.
7 e ne abbiamo calcolato la legge senza nemmeno preoccuparci di dire su quale spazio di
probabilità la presunta v.a. 7 fosse definita. È inoltre chiaro che lo spazio di probabilità dello
schema successo-insuccesso dell'Esempio 1.22 non è adatto, perché esso descrive un numero
prefissato n di prove successive, mentre per studiare l'istante di primo successo T occorre poter
considerare un numero arbitrariamente grande di prove.
Non è però un problema grave. Si può infatti dimostrare che, data una distribuzione discreta
p, è sempre possibile costruire uno spazio di probabilità (fi, sì, P) ed una v.a. X su di esso, tali
che X abbia p come densità.
Ad esempio se x}, x2 • • • sono i numeri per cui p(x) > O, si può scegliere
fi = [xì, x2, - -.},
si = insieme delle parti di fi
e definire la legge di probabilità P({jc,-}) = p ( x t ) ; se su (fi, si, P) definiamola v.a. X : £2 -*• M
mediante X(x{) = xit X così definita ha p come densità perché P(X = xf) — p(x;).
Per questo motivo nel seguito saremo sempre meno espliciti nella descrizione dello spazio di
probabilità e ci accontenteremo di supporre che ne esiste uno sul quale certe v.a. sono definite.
La nozione più importante d'ora in avanti sarà quella di distribuzione di una v.a. Abbiamo
appena visto del resto che, data una distribuzione di probabilità discreta p, esistono sempre
uno spazio (£2, M, P) ed una v.a. X ivi definita che ha p come distribuzione; nei calcoli poco
importerà sapere come siano fatti esplicitamente (£2, si, P) e X.
2.2 Variabili aleatorie discrete e loro distribuzioni
37
Se X ha legge geometrica di parametro p, una formula utile è la seguente:
co
Da questa relazione si ricava facilmente una classica proprietà della distribuzione geometrica:
se m > O
P(X = k + m, X > k)
P(X = k + m\X > k) = —
(2,3)
P(X>k)
(\-p)k
La (2.13) è detta la proprietà di mancanza di memoria della distribuzione geometrica. La
ragione di questo nome è illustrata dall'esempio seguente.
Esempio 2.13 In uno schema successo-insuccesso supponiamo di non avere ottenuto alcun
successo nelle prime k prove. Qual è la probabilità di dover attendere ancora m prove per avere
il primo successo?
Se indichiamo con T l'istante di primo successo, allora con un attimo di riflessione si vede
che la probabilità richiesta non è altro che la probabilità condizionale P(T = k + m \ > k).
Poiché T - 1 è una v.a. geometrica, grazie alla (2.13) abbiamo
P(T = k + m\T > k)=P(T -I =k + m-\ - I > k) =
= P(T - 1 = m - 1) = P(T = m)'.
Dunque la probabilità di dover attendere per il primo successo ancora m prove è la stessa che
si avrebbe se le prime k prove senza successi non avessero avuto luogo.
Questa proprietà è del resto ovvia se si pensa che in uno schema a prove ripetute indipendenti
i risultati delle prime prove non danno informazioni sui risultati delle successive; dunque, se
le prime k prove non hanno dato successo, non si vede perché la probabilità di avere successo
nelle prove successive debba essere modificata.
La proprietà di mancanza di memoria è in realtà una caratteristica della distribuzione geometrica:
si può dimostrare che se una v.a. gode di questa proprietà ed è a valori interi > O, allora si tratta
necessariamente di una v.a. di legge geometrica (in esercizio, per chi volesse, non è diffìcile).
Osservazione 2,14 Spesso in un gioco che consiste in prove ripetute indipendenti (lotto,
roulette,... ) i giocatori usano la tecnica di giocare sugli eventi in ritardo. Cioè, ad esempio, di puntare sistematicamente su un numero al lotto che non esca da molte settimane. Se le
prove ripetute sono indipendenti, è chiaro che questa tecnica non ha fondamento, a causa della
proprietà di mancanza di memoria della legge geometrica, per la quale la probabilità di dover attendere un certo numero di estrazioni l'uscita di un numero non dipende dal ritardo del numero.
I giocatori che usano questa tecnica sostengono però che se, ad esempio, un numero al lotto ha