Torino 2013_Lezione Marco

Le interazioni di spin a stato solido:
chemical shift e interazione dipolare
Marco Geppi
Dipartimento di Chimica e Chimica Industriale
Università di Pisa
[email protected]
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
NMR in soluzione vs. NMR di solidi
Soluzione
Larghezza di riga < 1 Hz
2 kHz
Solidi
Larghezza di riga ≈ 50 kHz
125 kHz
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
NMR a stato solido: timeline
“Scoperta” dell’NMR:
primo esperimento
realizzato su una
paraffina solida
1946
MAS
FT
CP
1958
1966
1972
Bassa Risoluzione
Combinazione CP-MAS-HPD
(nascita effettiva dell’NMR a
stato solido in alta risoluzione)
1976
Alta Risoluzione
Analisi di FID 1H
Cristalli singoli
Tecniche speciali che
richiedono
strumentazione dedicata
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
2011
L’equazione di Schrödinger
Il modello “vettoriale”, basato sulla fisica classica, è utile per comprendere molti aspetti
dell’NMR. In molti casi, tuttavia, esso si rivela inadeguato. Per questo, e per comprendere
meglio a cosa corrisponde il fenomeno NMR in termini di energia degli stati di spin, è
necessario far ricorso al modello quanto-meccanico.
Occorre partire dalla descrizione dell’Hamiltoniano del sistema. Questo può sempre essere
fattorizzato in una parte che dipende solo dalle coordinate spaziali e una solo dalle
coordinate di spin. Solo la seconda è rilevante ai fini dell’NMR.
In assenza di interazioni dipendenti dal tempo, gli autostati e le energie di un sistema di spin
possono dunque essere trovati risolvendo l’equazione di Schrödinger indipendente dal
tempo:
Ĥ è l’Hamiltoniano di spin del sistema,
Ĥψ = Eψ
E sono le energie degli stati (autovalori)
ψ sono le funzioni d’onda degli stati (autovettori)
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Hamiltoniano Zeeman
Hamiltoniano Zeeman: descrive l’interazione tra
lo spin nucleare e il campo magnetico esterno
(
Iˆ = Iˆx , Iˆy , Iˆz
)


ˆ
Ĥ 0 = − µ̂ ⋅ B0 = −γ I ⋅ B0 = −γ B0 Iˆz
→ operatore momento angolare di spin

B0 = ( 0, 0, B0 ) → campo magnetico esterno, diretto lungo l’asse z
Soluzioni dell’equazione di Schrödinger
Em = −γ B0 m
m → numero quantico che assume 2I+1 valori,
pari a -I, -I+1,… I
I → numero quantico di spin nucleare
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
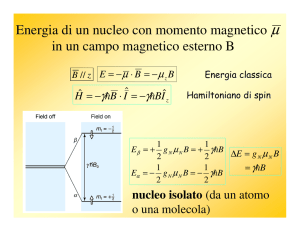
Gli stati Zeeman
Nel caso più semplice, quello di uno spin I=1/2, le
due autofunzioni che risolvono l’equazione di
Schrödinger (stati Zeeman), sono indicate con i
simboli |α> e |β>
m = -1/2
ΔEα → β = γ B0 = ω 0
ω0 = Frequenza di Larmor
m = +1/2
€
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Le interazioni “interne”
Gli spin nucleari non sono “isolati” e quindi non interagiscono solo con il campo magnetico
esterno, ma anche con “l’ambiente” che li circonda.
Queste interazioni sono dette “interne”, in quanto non coinvolgono nessun campo esterno, ed
hanno luogo tra lo spin nucleare e i campi magnetici o elettrici locali, generati ad esempio da
altri nuclei o dagli elettroni.
L’Hamiltoniano totale (trascurando l’interazione con il campo di radiofrequenza, che ha luogo
solo durante il breve periodo dell’impulso) può essere scritto come:
Ĥ = Ĥ 0 + ∑ Ĥ int
int
dove Ĥint sono i vari Hamiltoniani “interni”
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Hamiltoniani interni: espressione generale
I vari Hamiltoniani interni rappresentano
l’interazione del momento magnetico nucleare
con un campo locale ed hanno quindi la
stessa formula generica, simile a quella
dell'Hamiltoniano Zeeman
Ĥ int
dove

ˆ
= −γ I ⋅ Bloc


Bloc = A loc ⋅ T
Aloc è un tensore che descrive l’interazione

T
è un vettore che rappresenta l’origine del campo locale
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
La teoria delle perturbazioni
Generalmente il termine Zeeman è di gran lunga quello più importante. E’ quindi possibile
considerare i vari termini Ĥint come “perturbazioni” di Ĥ0.
Gli autostati dell’Hamiltoniano perturbato
sono gli stessi di Ĥ0.
Teoria delle perturbazioni
Le energie sono quelle “Zeeman” corrette
dai termini perturbativi.
Solo la parte secolare di Ĥint, cioè quella
che commuta con Ĥ0, contribuisce alla
correzione dell’energia.
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
La teoria delle perturbazioni
Ĥ 0 ψ 0 = E0 ψ 0
Eq. di Schrödinger per l'Hamiltoniano Zeeman
Ĥ ψ 0 = E ψ 0
Eq. di Schrödinger per l'Hamiltoniano totale (Zeeman + perturbazioni)
Ĥ = Ĥ 0 + ∑ Ĥ int ≅ Ĥ 0 + ∑ Ĥ intsec = Ĥ 0 + Ĥ1
int
int
⎡ Ĥ 0 , Ĥ intsec ⎤ = Ĥ 0 ⋅ Ĥ intsec − Ĥ intsec ⋅ Ĥ 0 = 0
⎣
⎦
E = E0 + E1
Ĥ1 ψ 0 = E1 ψ 0
Approssimazione secolare
Definizione dei termini secolari
(commutazione con l'Hamiltoniano Zeeman)
Energia totale (somma dell'energia Zeeman e di quella dovuta alle perturbazioni)
Eq. di Schrödinger per l'Hamiltoniano perturbativo
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Interazioni interne: schermo chimico
(chemical shift)
Interazione magnetica
indiretta tra gli spin nucleari e
il campo magnetico esterno
attraverso gli elettroni
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Interazioni interne: dipolo-dipolo
Diretta (dipolare)
Interazione magnetica diretta
tra spin nucleari
Indiretta (scalare, J-coupling)
Interazione magnetica
indiretta tra spin nucleari,
attraverso gli elettroni di
legame
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Interazioni interne: quadrupolare
Interazione elettrica tra nuclei con
spin > 1/2 (“quadrupolari”) e i
gradienti dei campi elettrici che li
circondano
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
L’Hamiltoniano di schermo chimico

ˆ
Ĥ cs = γ I ⋅ σ ⋅ B0
σ è il tensore di schermo
⎛ σ
σ xy σ xz
xx
⎜
Iˆ ⋅ σ = Iˆx , Iˆy , Iˆz ⋅ ⎜ σ yx σ yy σ yz
⎜
⎜⎝ σ zx σ zy σ zz
(
)
)
σ xy σ xz ⎞
σ yy σ yz ⎟⎟
σ zy σ zz ⎟⎠
⎞
⎟
⎟ = Iˆxσ xx + Iˆyσ yx + Iˆzσ zx , Iˆxσ xy + Iˆyσ yy + Iˆzσ zy , Iˆxσ xz + Iˆyσ yz + Iˆzσ zz
⎟
⎟⎠
(
⎛ σ
σ xy σ xz
xx
⎜

Iˆ ⋅ σ ⋅ B0 = Iˆx , Iˆy , Iˆz ⋅ ⎜ σ yx σ yy σ yz
⎜
⎜⎝ σ zx σ zy σ zz
(
⎛ σ xx
σ = ⎜⎜ σ yx
⎜⎝ σ
zx
⎞⎛
⎞
⎟⎜ 0 ⎟
⎟ ⎜ 0 ⎟ = Iˆxσ xz + Iˆyσ yz + Iˆzσ zz B0
⎟⎜ B ⎟
⎟⎠ ⎝ 0 ⎠
(
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
)
)
(
)
⎡ Iˆx , Iˆz ⎤ ≠ 0
⎣
⎦
Ĥ cs = γ  Iˆxσ xz + Iˆyσ yz + Iˆzσ zz B0
La parte secolare di questo Hamiltoniano è:
⎡ Iˆy , Iˆz ⎤ ≠ 0
⎣
⎦
Ĥ cssec = γ σ zz B0 Iˆz
Ĥ cssec = −σ zz Ĥ 0
1
Eβ = + γ B0 (1 − σ zz )
2
1
Eα = − γ B0 (1 − σ zz )
2
Zeeman
Zeeman + c.s.
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
⎡ Iˆz , Iˆz ⎤ = 0
⎣
⎦
Zeeman
ΔEα → β = γ B0
ω = ω 0 = γ B0
Zeeman +
schermo chimico
ΔEα → β = γ B0 (1 − σ zz )
ω = ω 0 (1 − σ zz )
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Il “Principal Axes Frame”
σzz è un termine del tensore di schermo definito nel sistema di riferimento di laboratorio. In
quanto tale è dipendente dall’orientazione della molecola in tale sistema di riferimento
Molecole con una diversa orientazione spaziale hanno σzz diversi e quindi valori
diversi della frequenza NMR
E’ conveniente scrivere il tensore di schermo nel “sistema di riferimento degli assi
principali” (Principal Axes Frame - PAF), cioè quello nel quale il tensore è diagonale
Gli elementi diagonali di questo tensore prendono il nome di “componenti principali”
zPAF
yPAF
B0
θ
φ
Per definire l’orientazione del PAF
rispetto al sistema di laboratorio
si usano gli angoli di Eulero (θ, φ)
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
xPAF
Voglio scrivere σzz in funzione delle componenti principali, in quanto
queste dipendono solo dalle proprietà della molecola
⎛ σ xxPAF
σ zz = ( sin θ cos φ sin θ sin φ cosθ ) ⎜ 0
⎜
⎜⎝ 0
0
σ yyPAF
0
0 ⎞ ⎛ sin θ cos φ ⎞
0 ⎟ ⎜ sin θ sin φ ⎟
⎟ ⎜
⎟
PAF ⎟
σ zz ⎠ ⎝ cosθ ⎠
(
)
ω = ω 0 (1 − σ zz ) = ω 0 ⎡⎣1 − σ xxPAF sin 2 θ cos 2 φ + σ yyPAF sin 2 θ sin 2 φ + σ zzPAF cos 2 θ ⎤⎦
Abbiamo trovato la dipendenza esplicita della frequenza NMR da θ e φ
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
La precedente equazione può essere riscritta nella seguente forma:
1
⎡
⎤
ω = ω 0 ⎢1 − σ iso − Δ ( 3cos 2 θ − 1 + η sin 2 θ cos 2φ ) ⎥
2
⎣
⎦
1
1
σ iso = Tr ( σ ) = σ xxPAF + σ yyPAF + σ zzPAF
3
3
(
)
Δ = σ zzPAF − σ iso
η=
σ xxPAF − σ yyPAF
σ zzPAF
SCHERMO ISOTROPO
(media su tutte le orientazioni:
l’unico termine che contribuisce allo
spettro di un liquido)
ANISOTROPIA DI SCHERMO
ASIMMETRIA DI SCHERMO
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Lo “spettro di polvere”
Normalmente i campioni solidi analizzati mediante NMR si trovano sotto forma di
“polveri”, in cui tutte le orientazioni molecolari sono presenti in modo
equiprobabile (solido isotropo). Di conseguenza, tutti i valori degli angoli θ e φ
sono rappresentati.
Lo spettro di ciascuna molecola (in assenza di moti molecolari) corrisponde ad
una riga centrata ad una ben precisa frequenza, che dipende da θ e φ.
Lo spettro dell’intero campione è dato dalla somma degli spettri delle singole
molecole e la forma che assume prende il nome di “spettro di polvere”.
Per predire la forma di questo spettro, che dipende dalla forma del tensore di
schermo, occorre integrare l’espressione della frequenza di schermo su θ e φ.
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
η =0 (σxx = σyy)
simmetria assiale
η≠0
(σxx ≠ σyy)
yPAF//B0
B0
B0
zPAF//B0
xPAF//B0
xPAF=yPAF//B0
zPAF//B0
≈ 200 ppm per
Le discontinuità nello spettro corrispondono all’allineamento dei
tre assi principali con il campo magnetico esterno B0
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
13C!
In un campione reale sono presenti molti nuclei
chimicamente non equivalenti. Ciascuno di essi contribuisce
allo spettro totale con la sua forma di riga.
Anche considerando la sola interazione di chemical shift lo
spettro di polvere è normalmente privo di risoluzione
spettrale.
La forma di riga totale dovuta all’interazione di chemical shift è la risultante dei contributi
indipendenti di tutte le molecole del campione di polvere che si trovano a diverse
orientazioni rispetto al campo magnetico.
E’ questo un esempio di contributo disomogeneo alla larghezza di riga.
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Lo spettro di un cristallo singolo
Nel cristallo singolo tutte le molecole hanno la stessa orientazione rispetto al campo
magnetico esterno.
Grazie alla natura disomogenea dell’interazione di schermo chimico, lo spettro risulta
estremamente semplificato:
B0
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
L’Hamiltoniano dipolare
L’interazione diretta tra i momenti magnetici degli spin nucleari prende il nome di interazione
dipolare.
Anche l’interazione scalare (J-coupling) ha luogo tra i momenti magnetici degli spin nucleari, ma
in questo caso l’interazione è indiretta, “mediata” dagli elettroni di legame.
Hamiltoniano per l’accoppiamento dipolare
tra due spin I e S in coordinate cartesiane:
nel PAF:
⎛ d
−
⎜ 2
⎜
D = ⎜ 0
⎜
⎜ 0
⎜
⎝
0
d
2
0
−
⎞
⎟
⎟
0 ⎟
⎟
d ⎟
⎟
⎠
H D = −2Iˆ ⋅ D ⋅ Ŝ
0
d=
µ0 γ I γ S 
4π r 3
r è la distanza internucleare
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
La forza dell’accoppiamento dipolare dipende dalla distanza
tra i due nuclei (in particolare da 1/r3) e dall’orientazione
relativa dei vettori I e S rispetto al campo magnetico esterno.
Quest’ultima è contenuta implicitamente nella definizione di
PAF per D.
D è un tensore a traccia nulla, per cui la sua componente
isotropa è nulla. Questo è il motivo per cui l’interazione
dipolare non contribuisce allo spettro di liquidi.
Gli accoppiamenti dipolari possono essere di due tipi:
omonucleari
eteronucleari
gli spin I e S sono della stessa specie
gli spin I e S sono diversi
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Interazione dipolare eteronucleare
Se si considera una coppia di spin eteronucleare (I e S), le autofunzioni dell’Hamiltoniano
Zeeman sono date dal prodotto degli stati Zeeman dei singoli spin:
|αα> |αβ> |βα> |ββ>
Le cui energie Zeeman sono date da
EmI mS = −B0 ( mI γ I + mSγ S )
Se si “osserva” lo spin I, si hanno due transizioni degeneri:
|αα>
|αβ>
|βα>
|ββ>
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Zeeman
se
3cos2 θ −1 > 0
Zeeman
+
Dipolare
|ββ>
|βα>
Il termine dipolare differenzia
l'energia delle due transizioni
a cui dà luogo lo spin I
|αβ>
|αα>
Il termine correttivo all’energia di questi stati in seguito a
“perturbazione” dovuta all’accoppiamento dipolare è:
(
)
ED = −mI mS 3cos 2 θ − 1 d
Eβα − Eαα = Eββ − Eαβ = γ I B0
per mI=mS
per mI≠mS
(
)
(
)
1
ED = − d 3cos2 θ −1
4
1
ED = + d 3cos2 θ −1
4
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
La frequenza corrispondente alle due transizioni è dunque data da:
1
ω DI = ω 0I ± d ( 3cos 2 θ − 1)
2
Dove i segni + e - si riferiscono rispettivamente agli stati α e β dello spin S
L'espressione della frequenza di transizione è
estremamente simile a quella che avevamo trovato per
l'interazione di schermo chimico nel caso η=0
1
⎡
⎤
ω = ω 0 ⎢1 − σ iso − Δ ( 3cos 2 θ − 1 + η sin 2 θ cos 2φ ) ⎥
2
⎣
⎦
La frequenza di risonanza dipende dunque dall’orientazione del
vettore internucleare rispetto a B0 (angolo θ). Integrando su tutte le
possibili orientazioni e sommando il contributo delle due transizioni si
ottiene il seguente spettro NMR “di polveri”
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Interazione dipolare omonucleare
Se si considera una coppia di spin omonucleare (I1 e I2), le autofunzioni dell’Hamiltoniano
Zeeman sono ancora date dal prodotto degli stati Zeeman dei singoli spin.
Quando si considera l’effetto della perturbazione dovuta all’interazione dipolare la situazione
è del tutto simile a quella del caso eteronucleare.
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
CaSO4·2H2O
gipso
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Interazione dipolare omonucleare
Quando si considerano interazioni dipolari tra più di due spin la situazione nel caso
omonucleare è molto più complessa: gli stati si mescolano continuamente a causa di
meccanismi di tipo “flip-flop” e l’effetto sulla riga NMR è un consistente allargamento della
riga (decine di kHz), nella quale tuttavia non possono più essere individuati i contributi
individuali delle varie orientazioni molecolari (interazione omogenea).
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Solidi vs. liquidi
Chemical shift e J-coupling isotropi
(uniche interazioni con tensore a
traccia non nulla)
Spettro “risolto”
Molte informazioni perse a causa dei
moti molecolari
2 kHz
Chemical shift e J-coupling isotropi e
anisotropi, interazione dipolare e
quadrupolare
Scarsa risoluzione spettrale
Tutte le informazioni presenti
125 kHz
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013
Riferimenti bibliografici
NMR Generale
Levitt, M.H. (2001) Spin Dynamics. John Wiley & Sons: Chichester, UK.
Duer, M.J. (ed.) (2002) Solid-State NMR Spectroscopy—Principles and
Applications. Blackwell Science: Oxford.
McBrierty, V.J. and Packer, K.J. (1993) Nuclear Magnetic Resonance in Solid
Polymers. Cambridge University Press: Cambridge.
NMR a
stato solido
Schmidt-Rohr, K. and Spiess, H.W. (1994) Multidimensional Solid-State NMR
and Polymers. Academic Press: London.
Saitô, H., Ando, I., and Naito, A. (2006) Solid State NMR Spectroscopy for
Biopolymers: Principles and Applications. Springer: Dordrecht, The
Netherlands.
Enciclopedie
Harris, R.K. and Wasylishen, R.E., Eds. Encyclopedia of Magnetic Resonance
[online]. John Wiley & Sons. www.mrw.interscience.wiley.com/emrw/
9780470034590/home/
Webb, G.A. (ed.) (2006) Modern Magnetic Resonance. Springer: Dordrecht,
The Netherlands.
Marco Geppi - “Le interazioni di spin a stato solido: chemical shift e interazione dipolare” - 26/09/2013