L’interazione Zeeman nucleare
1
Hamiltoniano di spin:
Lo stato di una particella (nucleo o elettrone) è di una particella è descritta da una
funzione d’onda che include le variabili spaziali (coordinate delle particelle) e di
spin.
Data la separazione delle energie e di scale dei tempi tra gli stati elettronici
(funzione delle coordinate spaziali) e gli stati di spin, si possono considerare tutte
le interazioni elettrostatiche come parametri e descrivere lo stato delle particelle
sulla base delle sole coordinate di spin utilizzando solo operatori di spin.
Un sistema di spin è definito come l’insieme di particelle (nuclei o elettroni)
interagenti tra loro
L’Hamiltoniano di spin descrive le interazioni (magnetiche e di altro tipo) del
sistema di spin sulla base dei soli operatori di spin (nucleari ed elettronici).
2
Le interazioni descritte dall’Hamiltoniano di spin possono essere di due tipi:
• Interazioni isotrope: sono indipendenti dalla orientazione nello spazio del
sistema di spin considerato
• Interazioni anisotrope: dipendono dalla orientazione nello spazio del
sistema di spin considerato
Normalmente la orientazione del sistema di spin (la molecola contenete i nuclei
o gli elettroni spaiati) è definita in un sistema di coordinate di laboratorio nel
quale il campo magnetico è preso come asse z
3
Le interazioni tra gli spin e il campo magnetico o tra coppie di spin sono in
generale anisotrope ma:
• In fase liquida (soluzioni) a causa del rapido moto molecolare, le interazioni
anisotrope vengono mediate. Il valore medio risultante può essere nullo o
diverso da zero a seconda della interazione considerata.
• In stato solido, le molecole (il sistema di spin) sono ferme o si muovono
lentamente. La mediazione delle interazioni anisotrope non è presente e le
frequenze di risonanza dipendono dalla orientazione della specie considerata
rispetto ad un sistema di riferimento di laboratorio.
4
In stato solido si possono avere
Sistemi ordinati (cristalli) nei quali esiste un elevato ordine orientazionale cioè
tutte le molecole assumo la stessa orientazione o un numero limitato di
orientazioni.
Le frequenze di risonanza
dipendono
dalla
orientazione del cristallo
(perciò delle molecole in
esso contenute) rispetto al
campo B0
5
In stato solido si possono avere
Sistemi disordinati (amorfi o policristallini). Sono ad esempio soluzioni solide,
vetri, polveri policristalline. In questi casi esiste un disordine orientazionale e le
molecole assumono tutte le orientazioni, statisticamente equiprobabili.
Le frequenze di risonanza
si disperdono in tutto
l’intervallo possibile delle
varie
orientazioni
molecolari,
che
sono
equiprobabili
"Spettri di polveri"
6
Una situazione intermedia tra lo stato solido ordinato e lo stato liquido si ottiene
in sistemi liquidi parzialmente ordinati (cristalli liquidi). In questo caso le
molecole sono dotate di moto ma esiste una orientazione statistica media (non
tutte le orientazioni sono equiprobabili). Innalzando la temperatura si passa da
una fase ordinata a una fase isotropa.
Le
possibili
orientazioni
molecolari vengono mediate in
un cristallo liquido ma le
frequenze di risonanza non
coincidono con quelle di un
liquido isotropo (senza ordine
orientazionale)
7
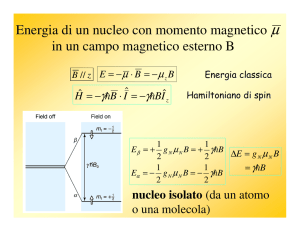
L’interazione Zeeman nucleare
L’interazione Zeeman è l’interazione tra lo spin ed il campo magnetico esterno.
L’Hamiltoniano Zeeman è:
)
)
H = −γI ⋅ B
= −γ (I x Bx + I y B y + I z Bz )
= −γI z B0
Si pone il campo magnetico
esterno B parallelo all’asse z del
sistema
di
riferimento
di
laboratorio
I nuclei sono sempre immersi nella nube
elettronica degli orbitali. Il campo
magnetico B induce una deflessione del
moto degli elettroni, che a sua volta
produce una circolazione netta delle
cariche elettroniche. Questa circolazione
induce un campo magnetico OPPOSTO a
B0.
8
Il campo totale sentito da un nucleo è quindi
B loc = B 0 + B indotto
Il campo indotto è proporzionale al campo esterno (in genere è di alcuni ordini
di grandezza inferiore) e può essere definito da:
B indotto = σ ⋅ B 0
Dove σ è in generale una matrice 3x3 detta Tensore di Chemical Shielding
(tensore di schermo chimico)
B indotto
Bxind σ xx σ xy σ xz 0
ind
= B y = σ yx σ yy σ yz ⋅ 0
B ind σ
B
σ
σ
zy
zz 0
z zx
Quindi il valore e la direzione del campo indotto in generale dipende dalla
orientazione della molecola rispetto al campo magnetico B0 (=asse z del
9
sistema di riferimento)
I tre assi principali del tensore σ rappresentano le tre direzioni particolari (indicate
spesso con X, Y, Z) che hanno questa caratteristica: se il campo B0 è diretto
lungo una di queste direzioni, il campo indotto è parallelo a B0 e il valore è pari a
B0 moltiplicato il valore principale riferito a quell’asse:
B indotto = σ xx B0
se B0 // X
= σ yy B0
se B0 // Y
= σ zz B0
se B0 // Z
Il chemical shielding isotropo è definito come la media dei valori principali del
tensore:
1
σ iso =
3
(σ
x
+σ y +σ z )
Si usa anche indicare due parametri, di Anisotropia (∆) e di Asimmetria (η) del
tensore di chemical shielding:
∆ = σ z − σ iso
(
σ
η=
x
−σ y )
σz
10
La frequenza di Larmor per il nucleo i-esimo è quindi diversa rispetto allo stesso
nucleo se fosse «isolato» e dipende dallo schermo chimico:
)
i
H i = −γI iz Bloc
= −γI iz B0 (1 − σ i )
ω0i = −γB0 (1 − σ i )
Essendo lo schermo chimico dipendente dal campo applicato, ne risulta una
dipendenza della frequenza di risonanza dalle condizioni sperimentali (cioè dal
campo magnetico dello spettrometro usato)
11
Per eliminare la dipendenza della gfrequenza di risonanza e dello schermo
chimico dal campo usato, cioè da fattori strumentali, si definisce la scala di
chemical shift δ:
ω − ωrif
δ=
⋅106
ωrif
espresso in parti per milione
(ppm)
Dove ωrif è la frequenza di risonanza di un campione standard di riferimento
(tipicamente TMS per i nuclei 1H), che per definizione risuona a 0 ppm
12
Essendo il chemical shift definito in relazione allo schermo chimico si ricva che
anche il chemical shift è anisotropo ed è descritto da un tensore di secondo
rango (anisotropia del Chemical Shift, CSA).
Il: chemical shift isotropo, osservato in soluzione, è dato dalla media dei tre
valori principali del tensore
δ iso =
1
(δ xx + δ yy + δ zz )
3
Anche per il tensore di chemical shift si definiscono il fattore di anisotropia e di
simmetria.
∆ cs = σ zz − σ iso
Due nuclei che hanno simili
chemical
shift
(cioè
simili
frequenze di Larmor) sono
separati maggiormente a campi
B0 maggiori.
η cs
(
σ
=
xx
− σ yy )
σ zz
La risoluzione spettrale aumenta
all’aumentare del campo B
13
Origine dello schermo chimico
Il tensore di schermo chimico σ deriva da diversi contributi:
σ = σ loc + σ vic + σ solv
Dove
• σloc indica il contributo derivante dalla densità elettronica sull’atomo stesso
• σvic indica il contributo da atomi e gruppi di atomi vicini
• σsolv indica il contributo del solvente
14
Il contributo locale al chemical shielding ha una parte diamagnetica
(schermatura) e una paramagnetica (deschermatura):
σ loc = σ dia + σ para
Il segno dei due
contributi locali è
opposto:
σ dia > 0
σ para < 0
Il contributo diamagnetico provoca una
schermatura del campo esterno
Il contributo paramagnetico provoca una
deschermatura del campo esterno
15
Il contributo diamagnetico locale è originato dalla distribuzione sferica di
elettroni attorno al nucleo. E’ presente in tutti gli atomi con configurazione a
guscio chiuso. Viene calcolata attraverso la Formula di Lamb:
σ dia =
µ0e 2
3me
∞
∫ rρ (r )dr
0
Dove ρ(r) è la distribuzione
radiale di densità elettronica
Per atomi isolati, con simmetria sferica, questo è l’unico contributo. E’
diamagnetico e proporzionale ala densità elettronica. Aumenta con l’aumentare
del numero atomico. Normalmente è un contributo piccolo rispetto ad altri.
16
Per il nucleo 1H, il termine locale diamagnetico è l’unico presente.
Questo spiega:
1) La piccola variazione di δ in uno spettro NMR di 1H (max 20ppm)
2) La dipendenza di δ dalla presenza di atomi elettron-attrattori nella molecola,
che causano una diminuzione di densità elettronica attorno al nucleo di
1H.(= diminuzione di schermo e aumento di chemical shift)
17
Nuclei diversi da 1H possono avere contributo locale paramagnetico,
derivante da elettroni in orbitali non di tipo s (che ha momento angolare nullo),
E’ un contributo che causa deschermatura (σ<0). Viene anche chiamato
paramagnetismo indipendente dalla temperatura (TIP), pe distinguerlo dal
paramagnetismo derivante da spin elettronici spaiati.
Il contributo paramagnetico viene calcolato come termine perturbativo al
secondo ordine dell’effetto del campo magnetico sugli stati elettronici;
)
)
)
H tot = H 0 + H ' '
• H0 è l’hamiltoniano in assenza di campo B
• H’’ è l’Hamiltoniano di interazione tra il
campo ed il sistema di particelle
Nel caso di perturbazione magnetica si considera un hamiltoniano di
perturbazione che dipende dall’interazione tra il momento magnetico orbitalico
ed il campo magnetico (modello di Ramsey) . Essendo il momento magnetico
proporzionale al momento angolare, l’Hamiltoniano perturbativo contiene
operatori di momento angolare:
)
)
H ''∝ L ⋅ B
L’Hamltoniano di perturbazione ha l’effetto di mescolare lo stato fondamentale
dell’atomo con gli stati eccitati.
18
I termini di perturbazione sulle energie orbitaliche e sulle funzioni portano a
calcolare i contributi allo schermo chimico con termini quali:
σ zzpara
)
)
)
)
2 Lz
2 Lz
0 3 n 0 Lz n
0 Lz n 0 r 3 n
r z
z
∝ ∑
+
En − E0
E n − E0
n
Dove la sommatoria si estende a tutti gli stati |n> eccitati e |0> indica lo stato
fondamentale. Dalla formula si ricavano alcune conseguenze:
• Gli stati con momento angolare nullo (L=0, orbitali tipo s) non contribuiscono
a σpara, quindi si considerano solo elettroni in orbitali p o d.
• Il contributo σpara è inversamente proporzionale a termini quali ∆E=En-E0
cioè alla differenza di energia tra lo stato eccitato e lo stato fondamentale.
Quindi è maggiore in atomi con stati eccitati a bassa energia.
Ad esempio in 1H gli stati eccitati (orbitali p o d) sono troppo ad alta energia
per contribuire. In 19F o 31P invece gli stati eccitati sono più vicini e si ha un
maggiore contributo σpara.
19
Il modello di Ramsey prevede che per un singolo elettrone il contributo σdia sia al
massimo di circa 20ppm, come si osserva in 1H (dove è l’unico contributo
significativo), ma il contributo σpara per alcuni nuclei può essere anche 10000 ppm.
ESEMPI:
13C
in alcani: la separazione ∆E tra orbitali σ e σ* è grande quindi si ha modesto
contributo σpara
13C
in chetoni: la separazione ∆E tra orbitali n e π* è piccola quindi si ha
significativo contributo σpara
Nella realtà, per i nuclei di idrogeno i due contributi locali sono spesso sovrastati
dal contributo dei gruppi vicini.
Per eteroatomi (tipicamente 13C) il contributo paramagnetico è rilevante: la
dispersione di chemical shift è di oltre 200ppm in 13C
20
Contributo dei gruppi vicini
Il contributo allo schermo chimico di gruppi di atomi prossimi al nucleo in esame
dipende dalla circolazione di elettroni indotta dal campo B sulle distribuzioni
elettroniche dei legami vicini.
Il campo magnetico B induce una circolazione di elettroni dei legami, che causa
la generazione di un dipolo magnetico. Questo dipolo magnetico indotto
produce un campo magnetico sul nucleo sommandosi o sottraendosi al campo
B esterno a seconda della orientazione dell’ nucleo rispetto al gruppo vicino.
L’effetto di schermo di legami
vicini è normalmente anisotropo
21
Si definiscono le suscettività magnetica parallela (χ//) e perpendicolare (χ⊥) al
legame considerato o all’asse di simmetria locale del gruppo di atomi vicini. Da
esse si ricava il momento di dipolo (µ
µ) indotto dal campo B0:
µ // ∝ χ // B 0
se B // asse di simmetria
µ ⊥ ∝ χ ⊥B0
se B ⊥ asse di simmetria
In generale la suscettività magnetica
dei gruppi vicini è anisotropa:
χ // ≠ χ ⊥
∆χ = χ // − χ ⊥
Il campo del dipolo indotto dipende dall’angolo tra la direzione del dipolo (direzione
del campo B0) e la distanza tra il centro del legame e il nucleo in esame:
(
1 − 3 cos θ )
σ ∝ ∆χ ⋅
2
r3
22
Il termine che dipende dall’angolo è positivo per θ> 54.7°
(
1 − 3 cos θ )
σ ∝ ∆χ ⋅
1− 3 cos 2 (ϑ )
2
r3
θ=54.7°
Lo schermo è positivo (schermaggio) o negativo (deschermaggio) a seconda del
segno del prodotto, che dipende da θ e dal segno di ∆χ.
23
Esempi: triplo legame C≡C:
χ // , χ ⊥ < 0
χ // >> χ ⊥
∆χ = χ // − χ ⊥ < 0
(
1 − 3 cos θ )
σ ∝ ∆χ ⋅
2
r3
σ > 0 (schermato)
se θ < 54.7°
Gli idrogeni alchinici sono
schermati (δ∼2)
σ < 0 (deschermato) se θ > 54.7°
24
χ // < χ ⊥
Esempi: doppio legame C=C e C=O:
χ⊥
χ⊥
∆χ = χ // − χ ⊥ > 0
(
1 − 3 cos θ )
σ ∝ ∆χ ⋅
2
r3
χ //
χ //
Gli idrogeni alchenici sono
deschermati (δ∼4-7)
Gli idrogeni aldeidici sono
deschermati (δ∼ 9-10)
25
Esempi:
Negli anelli aromatici è favorita la circolazione di elettroni nel piano dell’anello. Gli
areni presentano una forte anisotropia di suscettività magnetica e il valore
maggiore è nell’asse ortogonale al piano (χ//). Gli idrogeni periferici risento di un
aumento di campo magnetico (σ<0) cioè sono deschermati, e risuonano a
chemical shift maggiori.
Gli idrogeni aromatici sono
deschermati (δ∼6-9)
Gli idrogeni centrali, se presenti, mostrano elevato schermaggio
Idrogeni esterni: δ=9.3
Idrogeni interni: δ= -3
26
In soluzione le molecole ruotano velocemente e il valore di chemical shift è il
valore medio sulle orientazioni possibili. La presenza di forti effetti di gruppi vicini
determina il valore medio del chemical shift
27