I teorema di Euclide
Enunciato
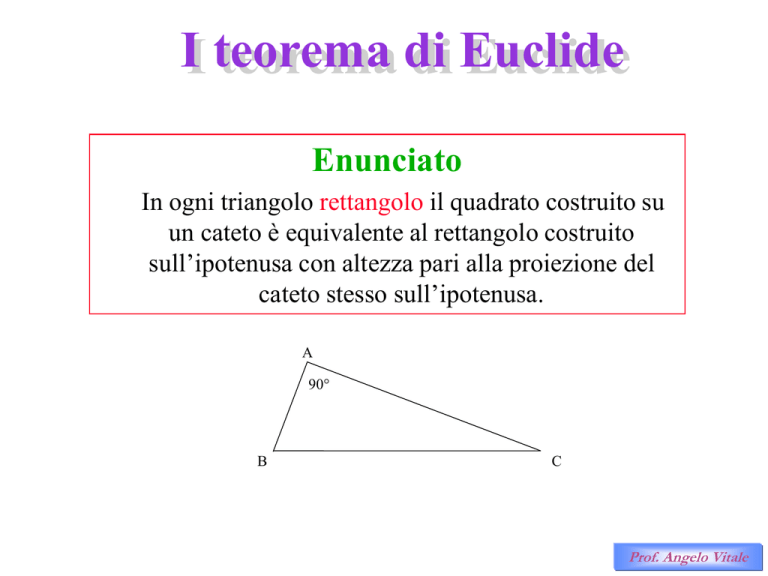
In ogni triangolo rettangolo il quadrato costruito su
un cateto è equivalente al rettangolo costruito
sull’ipotenusa con altezza pari alla proiezione del
cateto stesso sull’ipotenusa.
A
90°
B
C
Prof. Angelo Vitale
I teorema di Euclide
Enunciato
In ogni triangolo rettangolo il quadrato costruito su
un cateto è equivalente al rettangolo dell’ipotenusa e
della proiezione del cateto stesso sull’ipotenusa.
A
cateto
cateto
B
ipotenusa
C
Prof. Angelo Vitale
I teorema di Euclide
Enunciato
In ogni triangolo rettangolo il quadrato costruito su un
cateto è equivalente al rettangolo che ha per lati
l’ipotenusa e la proiezione del cateto stesso sull’ipotenusa.
BH = proiezione del cateto AB
sull’ipotenusa BC
A
cateto
cateto
B
H
C
Prof. Angelo Vitale
I teorema di Euclide
Dimostrazione
Costruiamo il quadrato sul cateto AB
A
B
H
C
Prof. Angelo Vitale
I teorema di Euclide
Dimostrazione
Costruiamo il rettangolo di lati BC e BH
A
B
H
C
H
Prof. Angelo Vitale
I teorema di Euclide
L’Enunciato afferma che:
L’area S1 e l’area S2 sono equivalenti
A
S1
H
B
S2
C
H
Prof. Angelo Vitale
I teorema di Euclide
Ribaltiamo il rettangolo S2
(la sua area non è cambiata)
A
S1
H
B
C
S2
Prof. Angelo Vitale
I teorema di Euclide
Prolunghiamo
il lato BF
D
A
S1
E
H
B
C
S2
F
G
Prof. Angelo Vitale
I teorema di Euclide
Prolunghiamo
il lato HG
D
A
S1
E
H
B
C
S2
F
G
Prof. Angelo Vitale
I teorema
di Euclide
Prolunghiamo
il lato ED
Fino ad
intercettare i
punti L e I
I
L
D
A
S1
E
H
B
C
S2
F
G
Prof. Angelo Vitale
BE = AB perché lati dello
stesso quadrato
Angolo in E = angolo in A
(retti per definizione)
Angolo EBL = angolo ABC
perché complementari
dello stesso angolo ABL
I
L
D
I due triangoli BLE e ABC sono
congruenti per il II criterio di
congruenza dei triangoli
Quindi sono uguali le
ipotenuse BL = BC
I teorema
di Euclide
A
E
S1
X
B
Ma essendo BC = BF
Per la proprietà transitiva ne
discende che:
BL = BF
X
H
C
S2
F
Prof. Angelo Vitale
Il quadrato S1 e il parallelogramma
ABLI (S3) sono equivalenti
per il II teorema di equivalenza dei
poligoni
Poiché hanno la stessa base AB e la
stessa altezza AD
I
L
Il rettangolo S2 e il parallelogramma S3
sono equivalenti per il II teorema di
equivalenza dei poligoni
Base BF=BL e altezza BH =BH
E
Quindi
S1 = S3 ma S3 = S2
Per la proprietà transitiva
S1 = S2
C.V.D.
I teorema
di Euclide
S3
D
A
S1
B
H
C
S2
CORSO DI
MATEMATICA
F
Prof. Angelo Vitale