Il primo teorema di Euclide
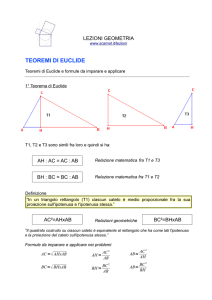
1° teorema di Euclide
In ogni triangolo rettangolo ciascun cateto è medio proporzionale tra la sua proiezione sull'ipotenusa e l'ipotenusa
dimostrazione I teor di Euclide.fig
LEGENDA
AC cateto
C
BC cateto
AB ipotenusa
A
H
AH : AC = AC : AB
B
AH proiezione del cateto AC sull'ipotenusa BH proiezione del cateto BC sull'ipotenusa
BH : BC = BC : AB
CH altezza relativa all'ipotenusa
a cura di Giovanni Marchisio
1
Il primo teorema di Euclide
dimostrazione I teor di Euclide.fig
IL quadrato costruito sul cateto AC è equivalente al rettangolo avente per dimensioni l'ipotenusa AB e la proiezione :
del cateto AC sull'ipotenusa quindi :
AC x AC = AH X AB
Supponendo che AC x AC siano i medi di una proporzione e che AH x AB gli estremi possiamo scrivere la seguente proporzione:
AH : AC = AC : AB
Lo steso procedimento si può eseguire per il cateto BC e per la sua proiezione sull'ipotenusa BH
a cura di Giovanni Marchisio
2
Il primo teorema di Euclide
Argomenti correlati
Poligoni inscritti e poligoni circoscritti
(Un triangolo iscritto in una semicirconferenza è un triangolo rettangolo)
Relazione tra angoli al centro e angoli alla
circonferenza corrispondenti
(L'angolo alla circonferenza è la metà del corrispondente angolo al centro)
Punti notevoli di un triangolo
(Baricentro, ortocentro, circocentro, incentro) (Il circocentro di un triangolo rettangolo si trova nel punto medio dell'ipotenusa.) a cura di Giovanni Marchisio
3
Allegati
I teor di Euc.fig
dimostrazione I teor di Euclide.fig