LEZIONI GEOMETRIA
www.scamat.it/lezioni
TEOREMI DI EUCLIDE
Teoremi di Euclide e formule da imparare e applicare
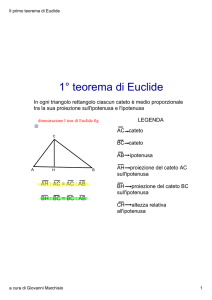
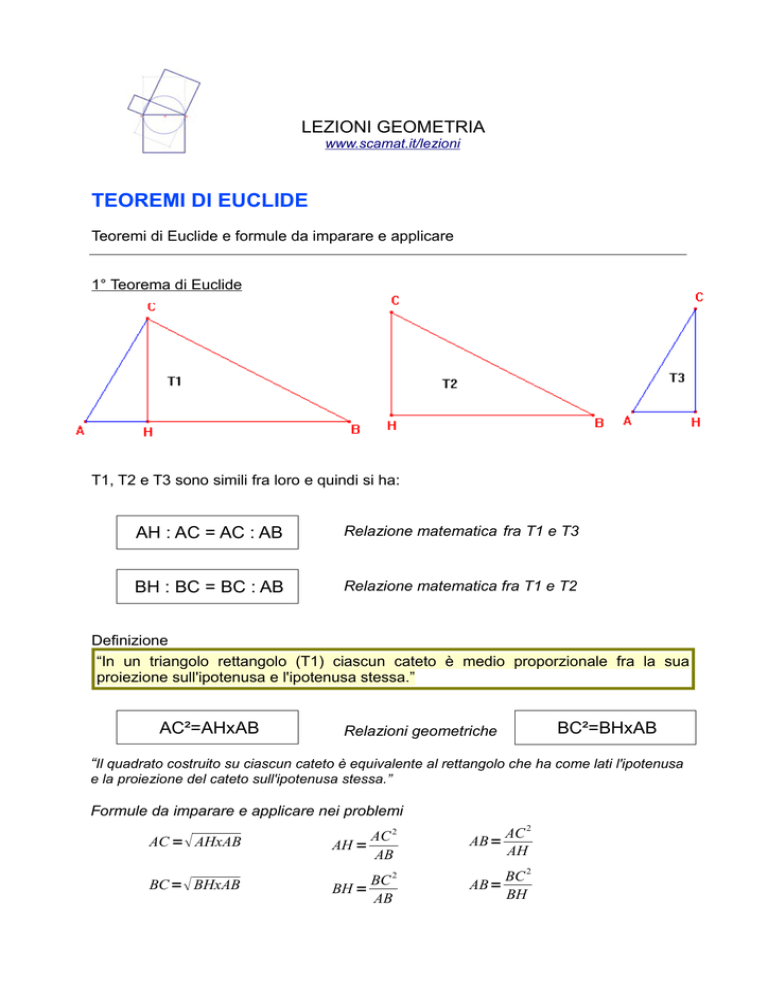
1° Teorema di Euclide
T1, T2 e T3 sono simili fra loro e quindi si ha:
AH : AC = AC : AB
Relazione matematica fra T1 e T3
BH : BC = BC : AB
Relazione matematica fra T1 e T2
Definizione
“In un triangolo rettangolo (T1) ciascun cateto è medio proporzionale fra la sua
proiezione sull'ipotenusa e l'ipotenusa stessa.”
AC²=AHxAB
BC²=BHxAB
Relazioni geometriche
“Il quadrato costruito su ciascun cateto è equivalente al rettangolo che ha come lati l'ipotenusa
e la proiezione del cateto sull'ipotenusa stessa.”
Formule da imparare e applicare nei problemi
AC = AHxAB
AC 2
AH =
AB
AB=
AC 2
AH
BC = BHxAB
BC 2
BH =
AB
AB=
BC 2
BH
LEZIONI GEOMETRIA
www.scamat.it/lezioni
2° Teorema di Euclide
T2 e T3 sono simili fra loro e quindi si ha:
AH : CH = CH : BH
Relazione matematica fra T2 e T3
Definizione
“In un triangolo rettangolo (T1) l'altezza relativa all'ipotenusa è media proporzionale fra
le proiezioni dei cateti sull'ipotenusa stessa.”
CH²=AHxBH
Relazioni geometriche
“Il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha come
lati le proiezioni dei cateti sull'ipotenusa stessa.”
Formule da imparare e applicare nei problemi
CH = AHxHB
CH 2
AH =
HB
2
HB=
CH
AH
LEZIONI GEOMETRIA
www.scamat.it/lezioni
TEOREMI DI EUCLIDE
Sintesi
1° Teorema di Euclide
Definizione
“In un triangolo rettangolo ciascun cateto è medio proporzionale fra la sua proiezione
sull'ipotenusa e l'ipotenusa stessa.”
AC²=AHxAB
BC²=BHxAB
AC = AHxAB
AC 2
AH =
AB
AC 2
AB=
AH
BC = BHxAB
BC 2
BH =
AB
AB=
BC 2
BH
2° Teorema di Euclide
Definizione
“In un triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale fra le
proiezioni dei cateti sull'ipotenusa stessa.”
CH²=AHxBH
CH = AHxHB
CH 2
AH =
HB
HB=
CH 2
AH