I problemi classici della geometria non risolubili con riga e compasso.
Pietro Romano
Liceo Scientifico Statale “Leonardo” - Giarre
Introduzione.
Uno degli argomenti più interessanti della geometria è quello delle costruzioni con riga e compasso.
La limitazione a questi oggetti risale all’antichità, sebbene gli stessi Greci facessero uso anche di
altri strumenti.
Per alcuni problemi (citiamo i più importanti: duplicazione del cubo, trisezione dell’angolo,
costruzione dell’ettagono regolare e quadratura del cerchio), malgrado gli innumerevoli tentativi,
non si riusciva però a trovare alcuna soluzione. Il protrarsi nel corso dei secoli di questi insuccessi,
cominciò a far ritenere che si trattasse di problemi senza soluzione; la ricerca si spostò allora nella
direzione di dimostrare l’impossibilità della soluzione.
In queste pagine, viene presentato un breve riassunto dei passaggi salienti che hanno permesso il
conseguimento di questo notevole risultato.
La trisezione dell’angolo col metodo di Archimede.
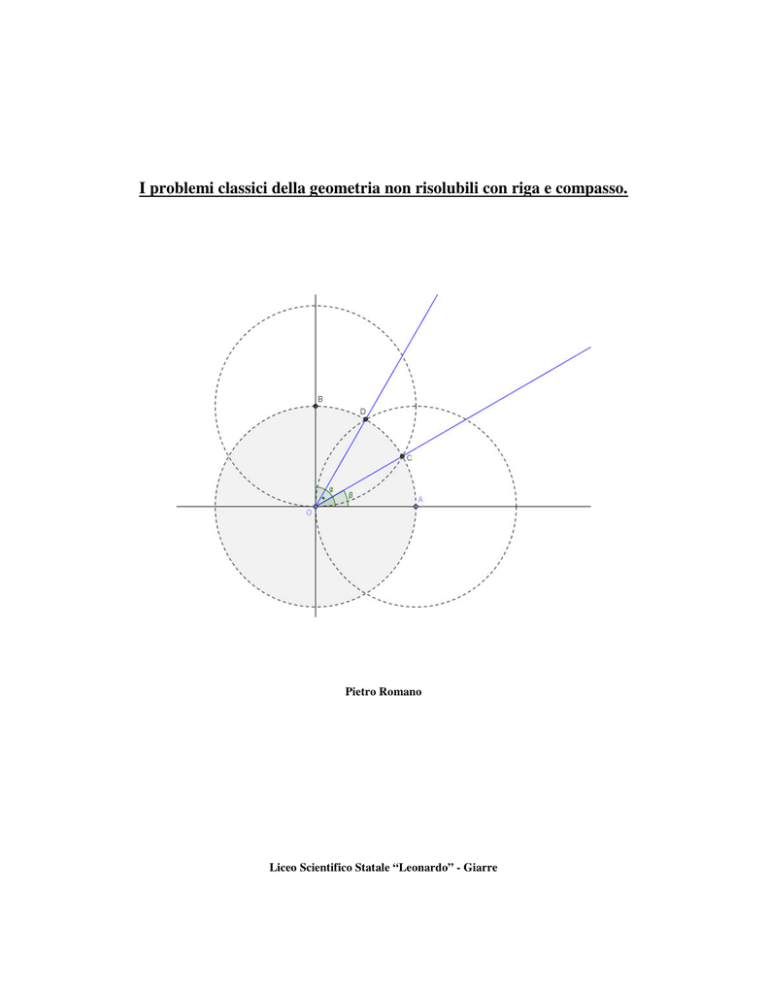
Cominciamo subito col far vedere una costruzione (fig. 1),dovuta ad Archimede, che permette di
trisecare un angolo arbitrario α . Assegnato α , si traccia una circonferenza arbitraria c con centro
in O, individuando i punti P e Q sulle due semirette di α . Si prolunghi inoltre OP dalla parte di O.
Si segna sulla riga un segmento O 'P '= OP e si traccia il segmento passante per Q tale che P 'si
mantenga su c e O ' sul prolungamento di OP . L’angolo β = OO '
P ', come si può facilmente
dimostrare, risulta pari ad α .
3
Figura 1: la trisezione dell'angolo (Archimede)
Questa costruzione sembra negare quanto affermato in premessa. Il punto è che non sono state
rispettate le regole, che impongono il solo utilizzo di riga e compasso. Staccando sulla riga un
segmento O 'P '= OP abbiamo violato le regole: la riga è infatti diventato uno strumento graduato.
Impostazione del problema.
La questione resta aperta, in quanto, se la costruzione esposta non risolve il problema, come si può
escludere il fatto che non ne esista una, rispettosa delle limitazioni tradizionalmente imposte, che
invero sia in grado di farlo?
Nel corso dei secoli si è continuato a ricercare in tal senso, ma senza alcun esito. Cominciò a farsi
strada l’idea che il problema fosse insolubile. Ma come dimostrarlo?
Il fatto di cominciare a ritenere che il problema non avesse soluzione, cominciò ad orientare la
ricerca nella direzione di cercare di caratterizzare in modo chiaro e definito ciò che può realmente
essere realizzato con riga e compasso, per poi far vedere che i problemi in questione non rientrano
in questo ambito.
2
Questa impostazione condusse effettivamente a dimostrare l’impossibilità della soluzione e
vedremo come gli elementi caratterizzanti di questo percorso saranno, tanto per cambiare, i numeri!
Campi estesi di numeri costruibili. Duplicazione del cubo.
Dati due segmenti, a e b, con costruzioni geometriche elementari siamo in grado di ottenere
segmenti la cui lunghezza è a + b , a − b , a ⋅ b , a . Se a e b sono numeri reali dati, il risultato di
b
ognuna delle operazioni indicate (dette operazioni razionali) è ancora un numero reale. In fig. 2,
riportiamo come esempio la costruzione di a :
b
Figura 2: costruzione di a
b
.
Si viene così a determinare un campo di numeri. I numeri razionali, i reali, i complessi costituiscono
campi di numeri.
Se iniziamo dal considerare un segmento di lunghezza 1, con le operazioni razionali ( +, −, ⋅,:)
siamo in grado di costruire segmenti la cui misura è espressa da un qualunque numero dell’insieme
dei numeri razionali. Ad esempio, per costruire un segmento di lunghezza 2 , è sufficiente
3
costruirne uno di lunghezza 2, uno di lunghezza 3, quindi dividerli col metodo descritto in fig. 2.
Con le sole operazioni razionali, non risulta però possibile estendere il campo dei razionali.
Indichiamo con C0 ( ≡ ) il campo numerico così costruito.
L’operazione, anch’essa costruibile con riga e compasso, e che ci permette di estendere il campo
C0 , è la radice quadrata. La figura che segue illustra la costruzione di x :
Figura 3: costruzione di
x.
3
Si dispongono consecutivamente un segmento OA = x ed un segmento AB = 1 ; si traccia quindi la
circonferenza di diametro OB (centro nel punto C) e la perpendicolare per A al diametro OB , che
incontra in D la circonferenza. Essendo il triangolo ODB rettangolo in D, il segmento DA , per il
II° teorema di Euclide, risulta appunto x . In generale, x non è in generale un numero razionale,
la qual cosa ci porta fuori dal campo numerico C0 dal quale siamo partiti. Consideriamo, ad
esempio, 2 : se fosse razionale, si potrebbe scrivere:
m
2=
n
Con m, n ∈ e che possiamo supporre primi fra loro. Elevando al quadrato, si ottiene m 2 = 2n 2 . Da
qui, segue che m 2 è pari e quindi anche m lo è. Allora si può scrivere
m = 2 p → m 2 = 4 p 2 = 2n 2 → n 2 = 2 p 2 , cosa che comporta che anche n 2 (e di conseguenza anche
n) è pari. Se m ed n sono entrambi pari, non sono primi tra loro, contro l’ipotesi fatta. Quindi, 2
non è razionale.
Vediamo di caratterizzare meglio il nuovo campo numerico. Fissato il valore di c0 (∈ ≡ C0 ) e
supposto che
c0 ∉ C0 (altrimenti non generiamo alcun nuovo numero!), costruito
c0 come da fig.
3, risulta semplice costruire con riga e compasso tutti i numeri del tipo a0 + b0 c0 , dove a0 e b0
appartengono a C0 . È inoltre semplice dimostrare che operazioni razionali su numeri di questa
forma conducono sempre a numeri della stessa forma (cioè del tipo a + b c0 ). È stato generato un
nuovo campo numerico C1 di numeri costruibili, per il quale vale sicuramente la condizione
C0 ( ≡
) ⊂ C1 ⊂
.
Per estendere il campo C1 appena generato, bisogna ripetere nuovamente le operazioni eseguite.
Bisogna cioè scegliere un valore c1 ∈ C1 tale che c1 ∉ C1 . I nuovi numeri avranno la forma
a1 + b1 c1 , con a1 , b1 ∈ C1 , e genereranno un nuovo campo numerico C2 di numeri costruibili, tale
che C0 ( ≡
) ⊂ C1 ⊂ C2 ⊂
. E così via.
È a questo punto lecito chiedersi: esiste un valore intero positivo h tale che il campo esteso Ch
genera ? La risposta è negativa e per dimostrarlo basterà portare anche un solo esempio. Il nostro
esempio sarà il numero 3 2 . Faremo vedere che questo numero non appartiene ad alcun campo
esteso Ch costruito a partire da C0 . Questa dimostrazione avrà una valenza doppia in quanto 3 2 è
soluzione dell’equazione x3 − 2 = 0 , che costituisce l’espressione algebrica del problema della
duplicazione del cubo1. Dimostrando che questo numero non appartiene ad alcun campo esteso Ch
costruito a partire da C0 , avremo di fatto dimostrato che 3 2 non è un numero costruibile e quindi
che la duplicazione del cubo non è eseguibile col solo uso di riga e compasso.
Cominciamo con l’osservare che 3 2 non può essere razionale, e ciò si motiva in modo analogo a
quanto visto per 2 . Quindi, 3 2 è reale.
1
Duplicare il cubo di lato 1 significa determinare il lato del cubo che ha volume doppio, cioè 2. Quindi, detto
lato, deve essere:
x questo
x3 = 2 .
4
Supponiamo ora che
3
2 appartenga ad un qualche campo esteso Ch ( h > 0 ) . La soluzione x sarà
allora del tipo x = a + b c , con a, b, c ∈ Ch −1 e
trova:
(a + b c )
3
c ∉ Ch −1 . Sostituendo questa soluzione in (3), si
−2 = 0→
(
) (
→ a 3 + 3ab 2 c − 2 + b3c + 3a 2b
)
c =0→
(4a)
→ ξ +η c = 0
Con ξ ,η ∈ Ch −1 . Per essere vera la (4a), si deve avere ξ = η = 0 . Se fosse infatti η ≠ 0 , si avrebbe
c =−ξ
ξ = 0.
η ∈ Ch −1 , contro l’ipotesi fatta. Quindi η = 0 e, conseguentemente (dalla (4a)), è anche
Osserviamo a questo punto che anche il numero reale x = a − b c risulta soluzione della (3) in
quanto, per sostituzione in (3), si giunge all’espressione, analoga alla (4a):
(4b)
ξ −η c = 0
Visto che, per quanto appena detto, è ξ = η = 0 , anche la (4b) è verificata. L’equazione (3) avrebbe
quindi due soluzioni reali, quando invece, essendo di grado 3, ne possiede una sola (le altre due
sono complesse coniugate). L’assurdo deriva dall’aver ammesso che la soluzione della (3)
appartenesse ad un qualche campo esteso Ch . Rimuovendo questa ipotesi, ne deriva che 3 2 non è
un numero costruibile con riga e compasso, o, in altre parole, non è possibile eseguire la
duplicazione del cubo.
Le equazioni cubiche
I ragionamenti svolti si sono rivelati proficui per risolvere la questione relativa alla duplicazione del
cubo. Per poter affrontare i problemi della trisezione dell’angolo e della costruzione dell’ettagono
regolare, bisogna preventivamente conoscere un importante teorema sulle equazioni cubiche: se
un’equazione cubica:
(5)
x3 + ξ x 2 + η x + ζ = 0
a coefficienti razionali non ammette radici razionali, allora nessuna delle sue radici è un
numero costruibile partendo dal campo razionale C0 .
Cominciamo col ricordare la relazione tra radici e coefficienti. Questa relazione segue
dall’uguaglianza x3 + ξ x 2 + η x + ζ = ( x − x1 ) ⋅ ( x − x2 ) ⋅ ( x − x3 )
Che conduce alle espressioni:
x1 + x2 + x3 = −ξ
x1 x2 + x1 x3 + x2 x3 = η
(6)
x1 x2 x3 = −ζ
Se, per ipotesi, nessuna delle radici x1 , x2 , x3 è razionale, procediamo per assurdo e supponiamo che
una radice appartenga ad un qualche campo esteso Ch . Ciò implicitamente significa che nei campi
che precedono Ch (cioè, da C1 a Ch −1 ) non vi sono radici della (5). Sia cioè:
x1 = a + b c
con a, b, c ∈ Ch −1 e
c ∉ Ch −1 . Sotto questa ipotesi, con un ragionamento analogo a quello svolto
prima per l’equazione x3 − 2 = 0 , anche x2 = a − b c è soluzione dell’equazione. La terza radice,
5
per la prima delle (6), si scrive allora: x3 = − x1 − x2 − ξ = −2a − ξ , e, non comparendo
c , risulta
x3 ∈ Ch −1 , che è contro l’ipotesi fatta.
Per effetto di questo teorema, ne consegue che una costruzione con solo riga e compasso non è
eseguibile se l’equivalente algebrico del problema è una cubica che non possiede soluzioni
razionali.
La trisezione dell’angolo
Sfruttando il teorema precedente, si dimostrerà ora che la trisezione dell’angolo in genere non è
eseguibile. In genere, in quanto, in situazioni particolari, essa è eseguibile. Ad esempio, per
l’angolo di 90°, la cui costruzione viene mostrata nella copertina. Un equivalente algebrico di
questo problema deriva dalla formula trigonometrica cos α = 4 cos3
α = 60° , posto cos
α
=
x
, dalla suddetta formula, si ottiene:
2
α
3
− 3cos
α
3
. In particolare, per
3
(7)
x − 3x − 1 = 0
Questa equazione cubica non ammette soluzioni razionali. Infatti, supponendo per assurdo che
x = m (al solito, con m, n ∈ e primi fra loro) sia una soluzione, per sostituzione avremo:
n
3
m3 = n 2 ( 3m − n )
m
m
3
2
3
(8)
− 3 − 1 = 0 → m − 3mn − n = 0 → 3
n
n
n = m ( m 2 − 3n 2 )
3
Le ultime due espressioni sono due differenti modi di esprimere il risultato ottenuto. Dalla prima,
essendo ( 3m − n ) ∈ , segue che m3 è divisibile per n 2 , e poiché per ipotesi m ed n sono primi fra
loro, deve essere necessariamente n = ±1 . Analogamente, dalla seconda delle (8), essendo
( n2 − 3m2 ) ∈ , n3 è divisibile per m, e quindi è anche m = ±1 . In definitiva, deve essere m n = ±1 .
Sostituendo questi valori in (7), si vede che nessuno dei due la soddisfa. Quindi, la (7) non ammette
soluzioni razionali e, conseguentemente non è possibile trisecare l’angolo di 60°.
La costruzione dell’ettagono regolare.
Come sopra, si dovrà in primo luogo trovare un equivalente algebrico del problema; quello di cui si
farà uso, si basa sui numeri complessi. I vertici dell’ettagono sono dati infatti dalle radici
dell’equazione:
z7 −1 = 0
(9)
con z = x + iy . Le soluzioni di questa equazione sono:
k ⋅ 360°
k ⋅ 360°
z = 7 1 = cos
+ i sin
, k = 0,1,..., 6
(10)
7
7
z7 −1
La prima ( k = 0 ) è z = 1 . Le altre derivano da:
= z 6 + z 5 + z 4 + z 3 + z 2 + z + 1 = 0 . Dividendo
z −1
1
1
1
3
3
2
per z , si trova: z + 3 + z + 2 + z + + 1 = 0 , che si può trasformare facilmente in:
z
z
z
3
2
1
1
1
1
z+
−3 z + + z +
−2+ z+
+1 = 0 →
(11)
z
z
z
z
→ x3 + x2 − 2 x − 1 = 0
6
1
avendo posto x = z + . Le soluzioni di questa equazione sono espresse dalla (10), però con k ≠ 0 .
z
1
k ⋅ 360°
k ⋅ 360°
Osserviamo che, per una proprietà dei numeri complessi, risulta: = cos
− i sin
,e
z
7
7
1
k ⋅ 360°
quindi: z + = x = 2 cos
. Allora, se una qualunque delle radici x è razionale, siamo in
z
7
grado di costruire l’ettagono regolare. Per comprendere meglio questo fatto, risolviamo la (10), ad
esempio con Derive (quindi, non con riga e compasso!) e rappresentiamo graficamente (piano di
Gauss) le soluzioni (fig. 4):
Figura 4: costruzione dell'ettagono regolare con Derive.
Immaginiamo dapprima che la soluzione razionale sia quella che si ottiene per k = 1 . Essendo già
nota la soluzione k = 0 , è noto il lato dell’ettagono; se la soluzione razionale è la k = 2 , per
ottenere il lato dell’ettagono, basta dimezzare l’angolo individuato da k = 0 e k = 2 ; se, infine, è
nota la k = 3 , per simmetria si costruisce anche k = 4 e quindi il lato.
Resta a questo punto da dimostrare che la (11) non ha soluzioni razionali.
Supponiamo allora che una soluzione della (11) sia razionale, cioè x = m , con m, n ∈ e primi
n
fra loro. Sostituendo in (11), si trova:
(12)
m3 + m 2 n − 2mn 2 − n3 = 0
Da qui, segue che m ammette per divisore n e viceversa. Essendo m ed n primi fra loro, deve esse
m
necessariamente m = n = ±1 → = ±1 . Nessuna di queste due soluzioni soddisfa la (11) quindi
n
l’ettagono regolare non è costruibile con riga e compasso.
La quadratura del cerchio.
Questo problema consiste nel costruire un quadrato avente area uguale a quella di un cerchio dato.
L’area del cerchio è data da π r 2 , dove π esprime il rapporto costante tra circonferenza e diametro
di un qualunque cerchio. Per un cerchio di raggio 1, la quadratura si traduce nel costruire il quadrato
di lato π , cosa che si può fare se è costruibile π . La questione della quadratura del cerchio si è
allora chiusa nel momento in cui si è dimostrato che π non solo è irrazionale (il che non sarebbe in
se un problema grave!), ma che è anche trascendente.
7
Un numero (reale o complesso) è trascendente se non è algebrico, cioè se non esiste alcuna
equazione della forma: an x n + an −1 x n−1 + ... + a1 x + a0 = 0 , con ai ∈ , di cui esso è soluzione.
Non è difficile far vedere che, tutti i numeri costruibili a partire dal campo C0 sono algebrici. Più
dettagliatamente, i numeri del campo C1 sono radici di equazioni di secondo grado, quelli del
campo C2 sono radici di equazioni di grado 2 2 = 4 , quelli del campo C p sono radici di equazioni di
grado 2 p . Per il campo C2 , se x = a1 + b1 c1 ne è il generico numero, risulta infatti:
x − a1 = b1 c1 → ( x − a1 ) = b12 ⋅ c1 → x 2 − 2a1 x + a12 − b12 ⋅ c1 = 0 →
2
→ x 2 + hx + f = 0
(13)
che è una equazione di 2° grado i cui coefficienti h = −2a1 ed f = a12 − b12 c1 sono elementi del
campo C1 , quindi ponibili nella forma a0 + b0 c0 , dove a0 , b0 ∈ C0 . Posto allora:
h = a + b c0
f = n + m c0
La
(13)
assume
la
forma:
(
)
x 2 + a + b c0 x + n + m c0 = 0 → x 2 + ax + n = − c0 ( bx + m ) .
Quadrando questa espressione, si ottiene una equazione di 4° grado a coefficienti razionali e quindi
trasformabile facilmente in una a coefficienti interi.
Cosa dire del numero π ?
Di esso, si può ottenere una stima partendo, ad esempio da un poligono regolare di n lati,
raddoppiandoli progressivamente (in fig. 5, il passaggio dal quadrato all’ottagono e quindi al
poligono a 16 lati).
Figura 5: approssimazioni successive mediante poligoni regolari inscritti a partire dal quadrato.
Se indichiamo con ln il lato del poligono regolare inscritto di n lati e con l2 n il lato di quello con
2n lati, si deduce la relazione:
8
l2 n = 2 − 4 − ln2
(14)
Se il cerchio ha raggio 1, dal triangolo BCD (fig. 6) si ha: AreaBCD =
Essendo: BH =
1
1
BH ⋅ CD = BC ⋅ BD .
2
2
2
2
AB ln
= , CD = 2 , BC = l2 n , BD = DC − BC = 4 − l22n , si ottiene:
2
2
1 ln
1
⋅ 2 = l2 n ⋅ 4 − l22n → ln2 = l22n ⋅ 4 − l22n → l24n − 4l22n + ln2 = 0 → l22n = 2 ± 4 − ln2
22
2
Dovendo la soluzione essere inferiore a 2, la soluzione col segno + va scartata e si ottiene la (14).
(
)
Figura 6: determinazione di
l2 n mediante ln .
Sapendo che l4 = 2 , si trova allora:
l8 = l23 = 2 − 2
l16 = l24 = 2 − 2 + 2
l32 = l25 = 2 − 2 + 2 + 2
(15)
........
l2h = 2 − 2 + ...... + 2
h −1 radici quadrate
Il perimetro del poligono avente 2h lati è quindi: P2h = 2 h ⋅ l2h . All’aumentare di h, la (16) fornisce
approssimazioni sempre migliori di π , cioè:
π = lim P2
h →∞
(16)
h
Si deve subito notare che l2h , e quindi anche P2h = 2 h ⋅ l2h , appartengono ad un campo esteso Ch −1 e
quindi sono numeri irrazionali ancorché algebrici. Al numero π si giunge però attraverso una
successione infinita di passaggi P22 , P23 ,...., P2h ,.... . Sarebbe naturale a questo punto pensare al π
{
}
come ad un numero irrazionale (è il limite di una successione infinita di numeri irrazionali!) ma non
9
viene spontaneo pensarlo come un numero algebrico (l’equazione algebrica dovrebbe avere grado
infinito!). Queste considerazioni, non costituiscono però una dimostrazione né della irrazionalità,
né della trascendenza del numero π 2.
La conclusione che traiamo alla luce di quanto detto, è che il problema della quadratura del cerchio
non ha pertanto soluzione.
2
L’irrazionalità di π , fu provata da Lambert nel 1761. La trascendenza fu dimostrata da Von Lindemann nel 1882,
utilizzando la stessa tecnica usata da Hermite (1873) per dimostrare la trascendenza di un altro numero importante: il
numero e . Queste dimostrazioni non sono certamente semplici ma sono comunque alla portata di chi possiede una
certa dimestichezza con gli strumenti dell’analisi.
10