Diapositiva 1

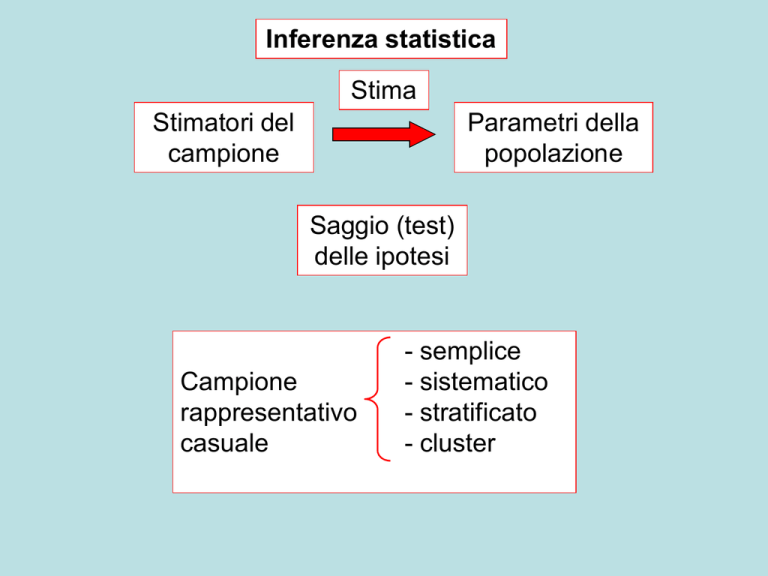
Inferenza statistica
Stima
Stimatori del
campione
Parametri della
popolazione
Saggio (test)
delle ipotesi
Campione
rappresentativo
casuale
- semplice
- sistematico
- stratificato
- cluster
Distribuzione campionaria della media
1) Estrazione di più campioni dalla popolazione.
2) Calcolo delle medie dei campioni.
3) Calcolo della media e della varianza delle medie dei
campioni.
Media delle medie=
media della popolazione
X  
Errore standard
(deviazione standard della media)
X 

n
Per n≥0,05N:
X 

N n
N 1
n
Teorema centrale del limite
n
2
X

N
(

,

)
lim  i
n   i 1
All’aumentare della dimensione del campione la
distribuzione campionaria della media approssima la
distribuzione normale, anche quando la popolazione
di partenza non era distribuita normalmente.
Approssimazione alla normalità adeguata per:
n≥ 30
Probabilità di un campione casuale con media X
in un intervallo:
X 

n
N=900; μ=20; σ=12; n=36
 X    20

12
X 

2
n
36
N=900; μ=20; σ=12; n=64 (>0,05N)
X 

n
N n
12

N 1
64
900  64 12 836

 (1,5)(0,96)  1,44
900  1
8 899
N=900; μ=20; σ=12; n=36
z1 
P(18  X  24)
z2 
Z
Area
X1   X

X 2  X

X
X
18  20
 1
2
24  20
2
2
P(18  X  24)  0,3413  0,4772  0,8185
81,85%
puntuale
Stima di un parametro
statistico di una popolazione
per intervallo
Stima puntuale: numero singolo, stima corretta se il
valore atteso corrisponde al parametro della popolazione.
( X stima puntuale corretta di  perchè  X   ;
s stima corretta di σ)
Stima per intervallo: probabilità (livello di confidenza o
fiduciale) che un intervallo di valori comprenda il parametro
sconosciuto della popolazione.
Intervallo di confidenza al 95% per la media della popolaz.:
P ( X  1,96 X    X  1,96 X )  0,95
P ( X  1,96 X    X  1,96 X )  0,95
Z=1,96
0,4750 x 2= 0,95 (95%)
P ( X  1,96 X    X  1,96 X )  0,95
N=1000; n=144;
X=100; σ=60
Intervallo di confidenza al 95% di μ?
P ( X  1,96 X    X  1,96 X )  0,95
P ( X  1,96 X    X  1,96 X )  0,95
Z=1,96
0,4750 x 2= 0,95 (95%)
N=1000; n=144 (>0,05N);
  X  1,96 X  X  1,96
 100  1,96
X=100; σ=60

n
N n

N 1
1000  144
 100  1,96(5)(0,93)  100  9,11
144 1000  1
60
Con un intervallo di confidenza del 95%:
90,89<μ<109,11
Se la distribuzione è normale, ma σ=? e n<30
non è possibile utilizzare la distribuzione di Z,
si usa la distribuzione t di Student
Per n>30 distribuzione di t = Z
G.L.
Gradi di libertà (GL)
Per distribuzione normale (Z):
Intervallo di confidenza al 95% per la media della popolaz.:
P ( X  1,96 X    X  1,96 X )  0,95
Per distribuzione t (σ=?; n<30)
Intervallo di confidenza al 95% per la media della popolaz.:
s
s
P( X  t
   X t
)  0,95
n
n
n=10;
X =5; s=1
Intervallo di confidenza al 95% di μ?
s
s
P( X  t
   X t
)  0,95
n
n
s
1
  X  2,262
 5  2,262
 5  2,262(0,316)  5  0,71
n
10
Cioè, al 95%: 4,29<μ<5,71
Distribuzione binomiale
Media della distribuzione
campionaria della proporzione
Errore standard della proporzione