10. Quadrilateri e punti medi - Liceo Scientifico G. Marinelli

10. Quadrilateri e punti medi
Problema
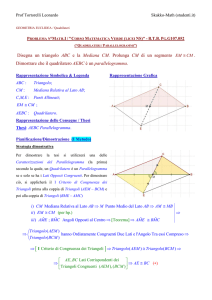
Sia ABCD un quadrilatero convesso generico. Su ogni lato
traccia il punto medio. Unendo i punti così trovati individuerai
un nuovo quadrilatero. Che tipo di quadrilatero hai ottenuto?
1. Leggi accuratamente il testo. Ci sono parole che non conosci? Scrivile qui sotto e prova a
cercarne il significato sul quaderno o sul libro.
Punto medio di un segmento =
Quadrilatero convesso =
2. Individua i DATI del problema e le relazioni tra di essi. Se possibile scrivili in linguaggio
matematico, altrimenti scrivili in linguaggio naturale, o anche in entrambi i modi. Poi fai un
disegno che tenga conto dei dati.
3. Osservando la figura così ottenuta quale quadrilatero ti sembra di aver costruito? Scrivi la tua
possibile risposta dopo avere eseguito qui sotto più di un disegno.
4. Prova a spiegare la tua risposta (Suggerimento: prova a disegnare le due diagonali, cosa
noti?).
5. Ora scrivi qui la tua risposta nel modo più corretto possibile, usando le parole corrette e
eventualmente dei simboli matematici e un disegno fatto con cura.
6. Se ora sei convinto dalla tua risposta prova a scrivere una SPIEGAZIONE (immaginati un tuo
compagno che non ci crede e prova a convincerlo).
44
PER IL DOCENTE
Quadrilateri e punti medi
Classe consigliata: 3^ media- biennio
superiore
Strumenti: carta e penna, eventualmente Cabri (o
Geogebra)
PREREQUISITI
• Punto medio di un segmento
• Conoscenze di base relative ai quadrilateri
• Similitudine tra triangoli
• Proprietà degli angoli individuati da rette parallele tagliate da una trasversale
• Teorema di Talete
(Questi ultimi tre prerequisiti non sono necessari, ma permettono di affrontare una dimostrazione più completa. Vedi
punto 5)
OBIETTIVO DELL’ATTIVITA’
•
•
•
Avviare alla congettura e alla sua validazione attraverso la dimostrazione
Cogliere varianti e invarianti in una situazione geometrica
Favorire l’acquisizione del linguaggio specifico
CONCETTI SOGGIACENTI (eventualmente sviluppabili)
•
Similitudine
L’attività si può sviluppare in una terza media e/o in un biennio superiore perché richiede requisiti
minimi e quindi favorisce il lavoro di gruppo. La costruzione porta alla formulazione di una
congettura non inizialmente prevedibile e può stimolare gli allievi a “convincere” i compagni
mettendo in atto capacità argomentative che successivamente verranno formalizzate in un
linguaggio più corretto.
1. Gli studenti possono cercare il significato dei termini che non conoscono o non ricordano.
2.
DATI
AM = MB
DP = PC
BN = NC
AQ = QD
3. Lo studente dovrebbe congetturare di aver ottenuto un parallelogramma
45
4. Spiegazioni:
CON SOTWARE DINAMICO: muovendo i vertici del quadrilatero ABCD si nota che i lati di MNPQ
sembrano sempre paralleli.
CON DISEGNO A MANO: Provando diversi esempi, anche “molto storti” la figura interna sembra
sempre un parallelogramma.
(E’ possibile che gli alunni disegnino solo quadrilateri con proprietà particolari e siano portati a fare
congetture restrittive tipo “è un rombo”, è opportuno sottolineare che il problema parla di
“quadrilatero” quindi è necessario provare anche quadrilateri non “speciali”.)
5. Risposte che è possibile aspettarsi dagli alunni, a seconda dei prerequisiti: per alcuni sarà
lecito attendersi una vera e propria dimostrazione argomentata, per altri una spiegazione “tra
pari” più immediata anche se non rigorosa.
DIMOSTRAZIONE “INGENUA”. Tracciando la diagonale AC “si vede” che il segmento MN è
parallelo ad AC e anche QP è parallelo ad AC. Quindi MN e QP sono paralleli tra di loro. Allo
stesso modo si capisce che MQ è parallelo a NP. Quindi il quadrilatero MNPQ è un
parallelogramma perché ha due coppie di lati paralleli. E’ opportuno sottolineare che i “si vede” non
sono vere dimostrazioni.
DIMOSTRAZIONE CON L’USO DI TRIANGOLI SIMILI. Il quadrilatero MNPQ è un
parallelogramma perché i lati che lo formano sono a due a due paralleli. Infatti tracciando la
diagonale AC i triangoli ADC e QDP sono simili, avendo l’angolo ADC in comune e i lati in
proporzione AD : QD = CD : PD. Di conseguenza gli angoli DAC e DQP sono uguali. Essi sono
formati da due segmenti AC e QP tagliati dalla trasversale AD, e quindi i segmenti QP e AC sono
paralleli. Per analoghe considerazioni effettuate sui triangoli BMN e BAC si può affermare che
MN//AC per la proprietà transitiva MN//QP. Allo stesso modo si dimostra che QM //PN.
DIMOSTRAZIONE CON IL TEOREMA DI TALETE. Disegnando la diagonale AC si può applicare
l’inverso del Teorema di Talete: se i segmenti staccati sulle rette AD e CD sono in proporzione (QD
e PD sono metà di AD e CD) allora le rette che li formano sono parallele. Quindi QP è parallelo ad
AC. Allo stesso modo si dimostra che MN è parallelo ad AC. Per la proprietà transitiva. MN è
parallelo a QP. Analogamente si ottiene che MQ è parallelo a NP.
46