Magie dei baricentri SCHEDA 4: Quadrilateri

Magie dei baricentri
SCHEDA 4: Quadrilateri - Parte II
Teorema
Dati un quadrilatero Q e una coppia di punti distinti R e S fuori dal piano di Q, al
quadrilatero dei baricentri rispetto ad essi corrisponde Q nell’omotetia di rapporto 3 e
centro il punto medio del segmento RS.
Dimostrazione
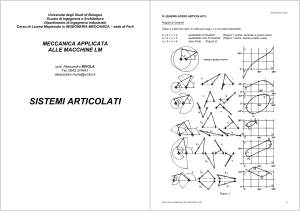
Siano:
- Ai con i=1,2,3,4 i vertici del quadrilatero Q e
R ed S due punti fuori dal piano di Q
Gi il baricentro del triangolo RSAi con i =
1,2,3,4
- G = G1G2G3G4 il quadrilatero dei baricentri
di Q rispetto a R ed S.
Poiché G1 è baricentro del triangolo RSA1, la
semiretta A1G1 contiene la sua mediana uscente
da A1 e pertanto interseca il lato RS nel suo
punto medio.
Analogamente, le semirette A2G2, A3G3, A4G4 intersecano il lato RS nel suo punto medio.
Detto M il punto medio del segmento RS, per una nota proprietà del baricentro, si ha:
MA1 = …..….. MG1
MA2 = …..….. MG2
MA3 = …..….. MG3
MA4 = …..….. MG4
Pertanto i punti A1, A2, A3 A4 sono i corrispondenti, rispettivamente di G1, G2, G3, G4, nella
…………………………………………...…………………………..…………………………….
Ne segue che il quadrilatero A1A2A3 A4 è il corrispondente del …...……….……………………
………………………………………………………………………………...…………………...
Corollario
Dati un quadrilatero Q e due punti R e S fuori dal piano di Q, l’area di Q è 9 volte l’area
del corrispondente quadrilatero dei baricentri.
Dimostrazione
………………………………………………………………...…………………………………
…………………………………………………………………..………………………………
……………………………………………………………………..……………………………
……………………………………………………………………..……………………………
……………………………………………………………………………………………………
Teorema
Siano dati un quadrilatero Q, due punti R e S fuori dal piano di Q. Sia  l’insieme dei
quadrilateri dei baricentri rispetto ad R ed S, ottenuti al variare di R e S.
Due qualsiasi quadrilateri di  sono congruenti tra loro e hanno i lati corrispondenti
paralleli.
Dimostrazione
……………………………………………………………………………………….…………
…………………………………………………………………………………………………
….……………………………………………………………………………………………..