Disegna un triangolo ABC e la Mediana CM. Prolunga CM di un

Prof Tortorelli Leonardo
Skakko-Math (studenti.it)
GEOMETRIA EUCLIDEA / Quadrilateri
PROBLEMA N°MATH.I / "CORSO MATEMATICA VERDE (LICEI NS)" - B.T.B. PG.G107.052
(“QUADRILATERI / PARALLELOGRAMMI”)
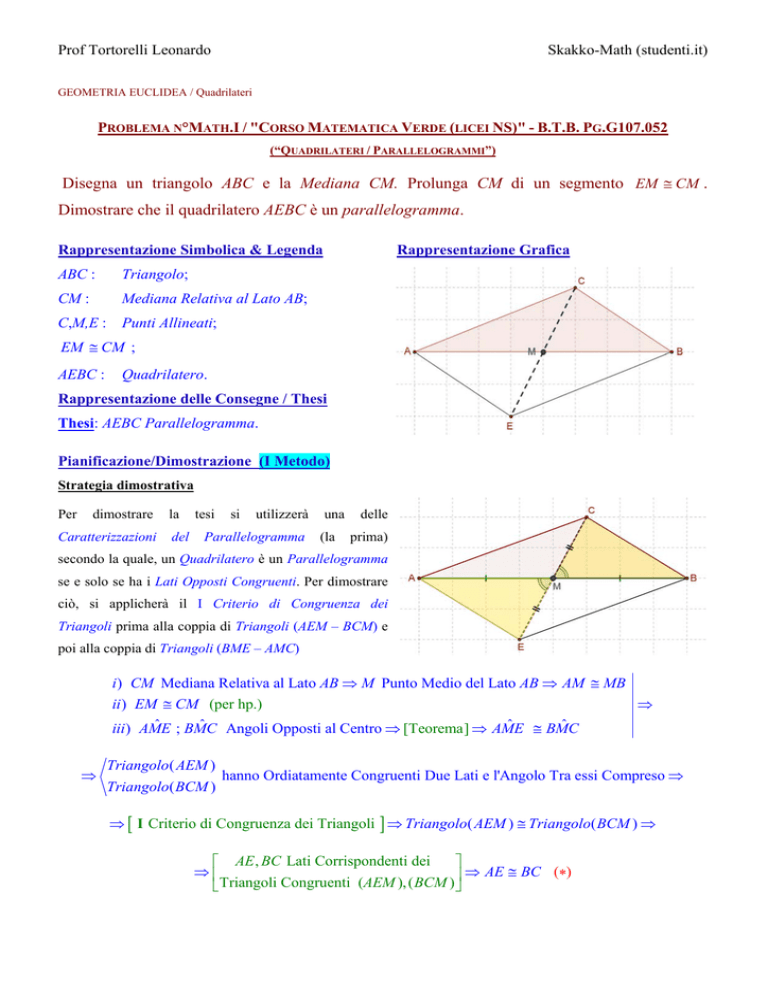
Disegna un triangolo ABC e la Mediana CM. Prolunga CM di un segmento EM  CM .
Dimostrare che il quadrilatero AEBC è un parallelogramma.
Rappresentazione Simbolica & Legenda
ABC :
Triangolo;
CM :
Mediana Relativa al Lato AB;
Rappresentazione Grafica
C,M,E : Punti Allineati;
EM  CM ;
AEBC :
Quadrilatero.
Rappresentazione delle Consegne / Thesi
Thesi: AEBC Parallelogramma.
Pianificazione/Dimostrazione (I Metodo)
Strategia dimostrativa
Per
dimostrare
Caratterizzazioni
la
del
tesi
si
utilizzerà
Parallelogramma
una
(la
delle
prima)
secondo la quale, un Quadrilatero è un Parallelogramma
se e solo se ha i Lati Opposti Congruenti. Per dimostrare
ciò, si applicherà il I Criterio di Congruenza dei
Triangoli prima alla coppia di Triangoli (AEM – BCM) e
poi alla coppia di Triangoli (BME – AMC)
i ) CM Mediana Relativa al Lato AB  M Punto Medio del Lato AB  AM  MB
ii ) EM  CM (per hp.)

ˆ ; BMC
ˆ Angoli Opposti al Centro  Teorema   AME
ˆ  BMC
ˆ
iii ) AME

Triangolo( AEM )
hanno Ordiatamente Congruenti Due Lati e l'Angolo Tra essi Compreso 
Triangolo( BCM )
  I Criterio di Congruenza dei Triangoli   Triangolo( AEM )  Triangolo( BCM ) 
 AE , BC Lati Corrispondenti dei


 AE  BC (*)

Triangoli Congruenti (AEM ), ( BCM ) 
Prof Tortorelli Leonardo
Skakko-Math (studenti.it)
Analogamente, sempre con il I Criterio di Congruenza
dei Triangoli si dimostra che:
Triangolo( AMC )  Triangolo( BME )
 AE, BC Lati Corrispondenti dei 

  AC  BE (**)
Triangoli Congruenti (AEM ),(BCM )
Mettendo insieme quanto dimostrato finora si ha che:
AE  BC (*)
 I Caratterizzazione 
 AEBC Quadrilatero con i Lati Opposti Congruenti  

AC  BE (**)
dei Parallelogrammi 
 AEBC Parallelogramma
Pianificazione/Dimostrazione (II Metodo)
Strategia dimostrativa
Per dimostrare la tesi si utilizzerà una delle Caratterizzazioni
del Parallelogramma (la terza) secondo la quale, un
Quadrilatero è un Parallelogramma se e solo se le due
Diagonali si intersecano nel loro Punto Medio.
i ) CM Mediana Relativa al Lato AB  M Punto Medio del Lato AB  AM  MB

ii ) EM  CM (per hp.)
 AM  MB  EM  CM  I Segmenti AB e EC si intersecano nel loro Punto Medio M 
 Le Diagonali del Quadrilatero AEBC si intersecano nel loro Punto Medio M 
 I Caratterizzazione 

  AEBC Parallelogramma .
dei Parallelogrammi 