E 4
CAPITOLO
L’algebra incontra la geometria:
primi passi nella geometria analitica
RIASSUNTO
Ricorda!
TEORIA
ESEMPIO
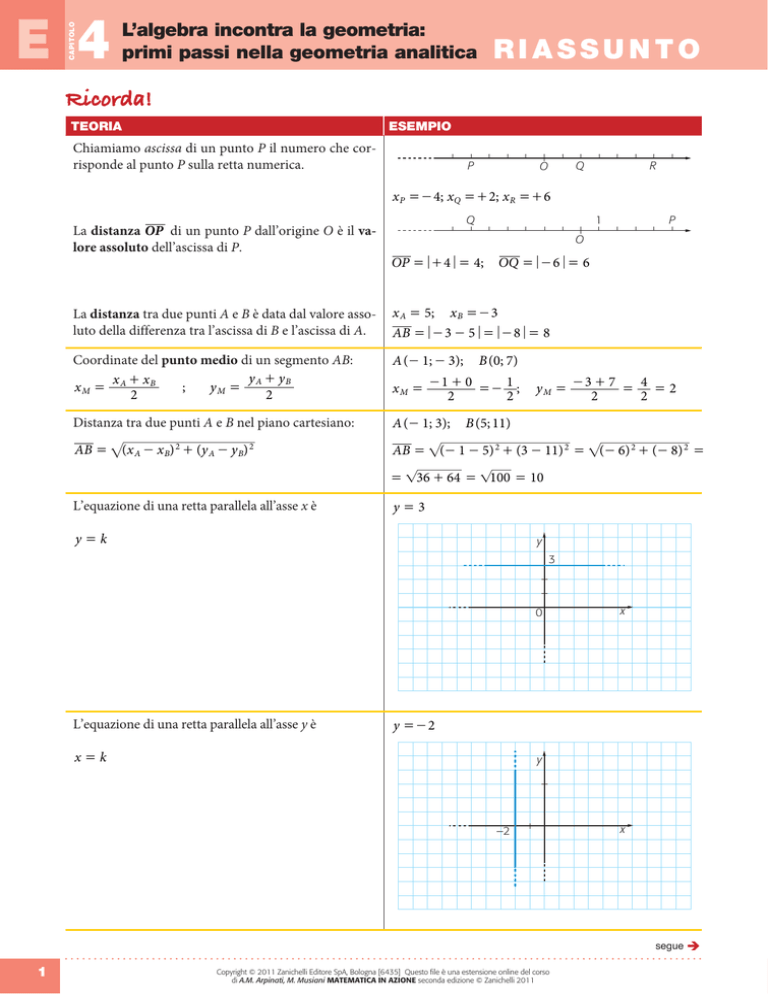
Chiamiamo ascissa di un punto P il numero che corrisponde al punto P sulla retta numerica.
P
Q
O
R
x P =- 4; xQ =+ 2; x R =+ 6
Q
La distanza OP di un punto P dall’origine O è il valore assoluto dell’ascissa di P.
O
OP = + 4 = 4;
OQ = - 6 = 6
La distanza tra due punti A e B è data dal valore assoluto della differenza tra l’ascissa di B e l’ascissa di A.
x A = 5; x B =- 3
AB = - 3 - 5 = - 8 = 8
Coordinate del punto medio di un segmento AB:
yA + yB
x + xB
xM = A
;
yM =
2
2
A (- 1; - 3);
xM =
Distanza tra due punti A e B nel piano cartesiano:
A (- 1; 3);
AB =
(x A - x B) 2 + (y A - y B) 2
B ( 0; 7)
-1 + 0
1
=- ;
2
2
AB =
=
L’equazione di una retta parallela all’asse x è
P
1
yM =
-3 + 7
4
= =2
2
2
B (5; 11)
(- 1 - 5) 2 + (3 - 11) 2 =
(- 6) 2 + (- 8) 2 =
36 + 64 = 100 = 10
y=3
y=k
y
3
0
L’equazione di una retta parallela all’asse y è
x
y =- 2
x=k
y
–2
x
segue
1
Copyright © 2011 Zanichelli Editore SpA, Bologna [6435] Questo file è una estensione online del corso
di A.M. Arpinati, M. Musiani MATEMATICA IN AZIONE seconda edizione © Zanichelli 2011
Î
CAPITOLO
E 4
L’algebra incontra la geometria:
primi passi nella geometria analitica
Ð segue
TEORIA
RIASSUNTO
ESEMPIO
L’equazione di una retta parallela passante per l’origine è
y = 3x
y
3
y = mx
1
x
1
Ogni funzione del tipo
y
y = mx + k
è rappresentata graficamente da una retta non parallela all’asse y.
Il fattore m, detto coefficiente angolare, indica la
pendenza della retta, mentre k è una costante che
fornisce l’ordinata del punto di intersezione fra la
retta e l’asse y.
Rette parallele hanno coefficienti angolari uguali.
x
0
y= 1 x+2
2
y=
1
x+2
2
y = 2x
e
y = 2x - 3
y
x
y = 2x – 3
y = 2x
Due rette perpendicolari hanno i coefficienti angolari
discordi con valori assoluti uno l’inverso dell’altro.
y =-
1
x+1
3
e
y = 3x
y
y=–1 x+1
3
y = 3x
x
segue
2
Copyright © 2011 Zanichelli Editore SpA, Bologna [6435] Questo file è una estensione online del corso
di A.M. Arpinati, M. Musiani MATEMATICA IN AZIONE seconda edizione © Zanichelli 2011
Î
CAPITOLO
E 4
L’algebra incontra la geometria:
primi passi nella geometria analitica
Ð segue
TEORIA
RIASSUNTO
ESEMPIO
Per trovare le coordinate del punto di intersezione tra
due rette non parallele si possono seguire due metodi:
quello grafico e quello algebrico.
Metodo grafico
Si tracciano le rette sul piano cartesiano con la massima precisione e si leggono sul grafico stesso le coordinate del punto in cui si intersecano.
Determiniamo il punto di intersezione tra le rette
x
y = + 1 e y = 4x - 10 .
3
y
P = (3; 2)
x
O
x
y = ––– + 1
3
Metodo algebrico
Si risolve l’equazione che si ottiene uguagliando l’ordinata del punto di intersezione delle due rette.
y = 4x – 10
Determiniamo il punto di intersezione tra le rette
y =- x + 3 e y = 2x + 6
- x + 3 = 2x + 6
- x - 2x =- 3 + 6
- 3x =+ 3 quindi x =- 1
Sostituiamo x =- 1 per esempio nella prima delle
due rette:
y =- x + 3 =- (- 1) + 3 = 1 + 3 = 4
Le coordinate del punto di intersezione sono
P ( - 1; 4)
y
y = 2x + 6
P(–1; 4)
O
segue
3
Copyright © 2011 Zanichelli Editore SpA, Bologna [6435] Questo file è una estensione online del corso
di A.M. Arpinati, M. Musiani MATEMATICA IN AZIONE seconda edizione © Zanichelli 2011
x
y = –x + 3
Î
CAPITOLO
E 4
L’algebra incontra la geometria:
primi passi nella geometria analitica
Ð segue
TEORIA
RIASSUNTO
ESEMPIO
Ogni funzione del tipo
y
y = kx2
è rappresentata graficamente da una curva detta parabola.
La costante k influenza l’apertura della parabola:
䊉
se k è maggiore di zero, la parabola si svolge nel primo e nel secondo quadrante;
䊉
se k è minore di zero, la parabola si svolge nel terzo e
nel quarto quadrante.
y = 1 x2
4
x
O
y
x
O
y=⫺
Ogni funzione del tipo
k
y=
(da cui si può facilmente ricavare xy = k)
x
è rappresentata graficamente da una curva detta iperbole.
y
Se k è maggiore di zero, la curva si svolge nel primo
e nel terzo quadrante;
䊉
se k è minore di zero, la curva si svolge nel secondo
e nel quarto quadrante.
y = 4x
x
O
Tale curva è simmetrica rispetto all’origine degli assi e
alle bisettrici dei quadranti.
䊉
1 2
x
4
y
4
y=⫺x
x
O
4
Copyright © 2011 Zanichelli Editore SpA, Bologna [6435] Questo file è una estensione online del corso
di A.M. Arpinati, M. Musiani MATEMATICA IN AZIONE seconda edizione © Zanichelli 2011