CAPITOLO
C 6 Dati e previsioni (1 parte)
RIASSUNTO
a
Ricorda!
ESEMPIO
Per raggruppare un insieme di dati si suddivide un
intervallo contenente tutti i dati in parti uguali e si
contano i dati appartenenti a ciascuno degli intervalli
così ottenuti.
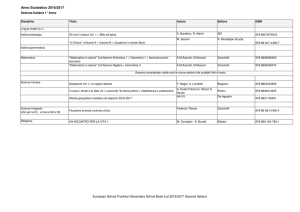
Peso in kg degli alunni di una classe: lo suddividiamo
di 10 kg in 10 kg.
37 38 39 39 41 42 42 42 45 45 50 51 52 52 56
frequenza
TEORIA
7
6
5
4
3
2
1
31 - 40
䊉
䊉
䊉
䊉
individuare la popolazione statistica da studiare;
individuare l’unità statistica;
raccogliere dati;
compilare tabelle di frequenza;
51 - 60
peso
Problema: quanti alunni della I B possiedono cani e
gatti?
Popolazione statistica: la classe I B.
Unità statistica: ogni alunno.
Dati: Arduini: due gatti
Bellomo: nulla
Bordoni: un cane
...
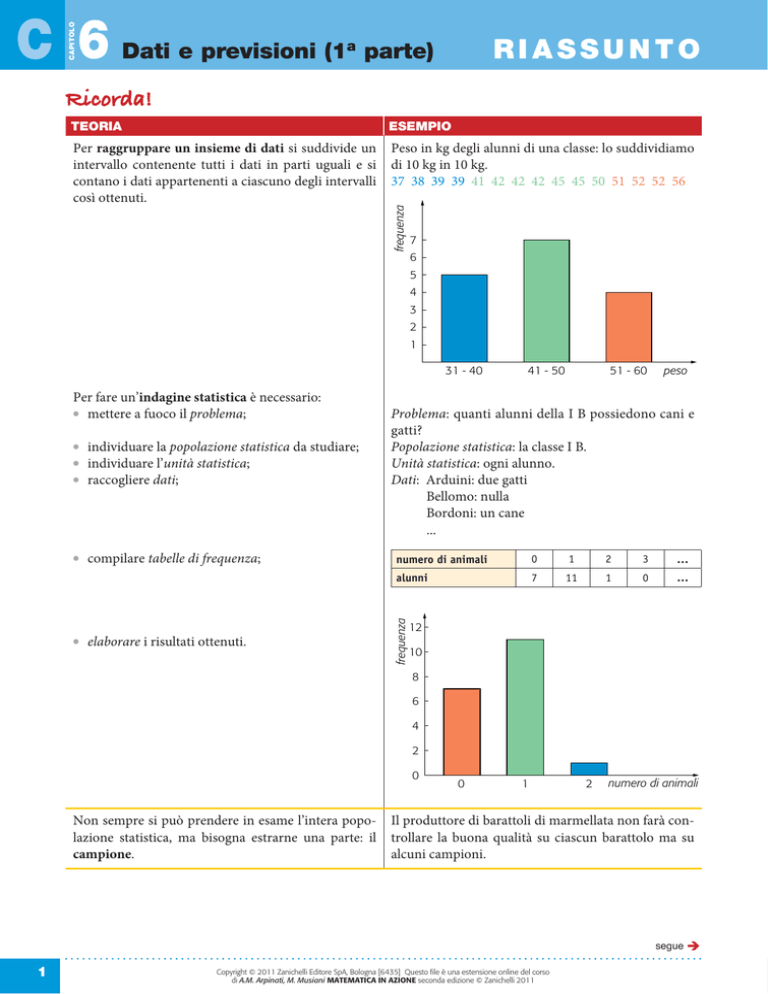
numero di animali
0
1
2
3
…
alunni
7
11
1
0
…
frequenza
Per fare un’indagine statistica è necessario:
䊉 mettere a fuoco il problema;
41 - 50
12
䊉
elaborare i risultati ottenuti.
10
8
6
4
2
0
Non sempre si può prendere in esame l’intera popolazione statistica, ma bisogna estrarne una parte: il
campione.
0
1
2
numero di animali
Il produttore di barattoli di marmellata non farà controllare la buona qualità su ciascun barattolo ma su
alcuni campioni.
segue
1
Copyright © 2011 Zanichelli Editore SpA, Bologna [6435] Questo file è una estensione online del corso
di A.M. Arpinati, M. Musiani MATEMATICA IN AZIONE seconda edizione © Zanichelli 2011
Î
CAPITOLO
C 6 Dati e previsioni (1 parte)
a
Ð segue
TEORIA
2
RIASSUNTO
ESEMPIO
In un insieme di dati può essere utile determinare alcuni indici di posizione:
䊉 la moda, che è il valore più frequente;
䊉 la mediana, che è il dato centrale (o la somma fra
i due dati centrali diviso due) in un insieme di dati
posti in ordine crescente (o decrescente).
Insieme di dati: i voti di Simone in matematica dall’inizio dell’anno.
6 4 5 7 6 6 7
Ordiniamoli:
4 5 A6B BB
6 6C 7 7
La moda è 6.
La mediana è 6.
La media aritmetica è la somma dei dati numerici divisa per il numero degli stessi dati.
La media è:
Il campo di variazione di un insieme numerico è la
differenza fra il dato massimo e il dato minimo.
Dato massimo = 7
Dato minimo = 4
Campo di variazione = 7 - 4 = 3
La probabilità di un evento è il rapporto fra il numero
dei casi a esso favorevoli e il numero dei casi possibili.
Se scegli un mese a caso fra i mesi dell’anno, la probabilità che il suo nome cominci con m è:
Numero dei mesi con iniziale m
2
1
=
=
Numero totale dei mesi
12
6
4+5+6+6+6+7+7
= 5, 86
7
Copyright © 2011 Zanichelli Editore SpA, Bologna [6435] Questo file è una estensione online del corso
di A.M. Arpinati, M. Musiani MATEMATICA IN AZIONE seconda edizione © Zanichelli 2011