Misura di potenze in
corrente alternata
OBIETTIVO: MISURA DI POTENZE IN CORRENTE ALTERNATA E CALCOLO DEL COSφ
MATERIALE:
1) 1) ALIMENTATORE IN CORRENTE ALTERNATA
1) BIPOLO PASSIVO DI TIPO OHMICO INDUTTIVO (R-L)
1) 1) AMPEROMETRO
1) VOLTMETRO
1) WATTMETRO
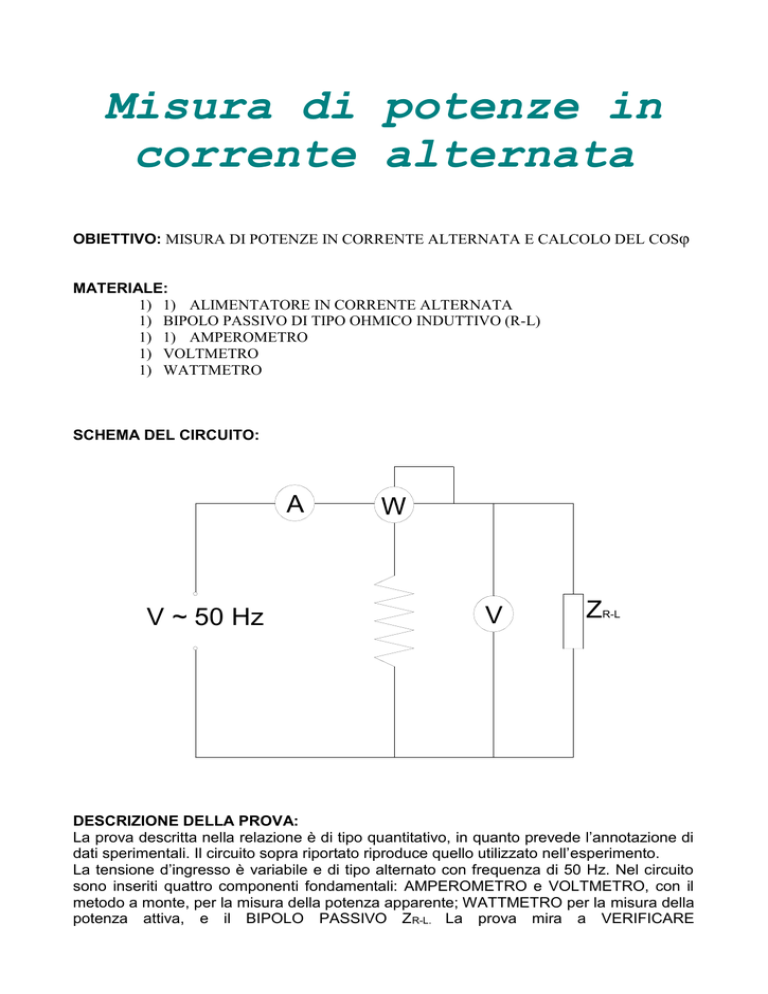
SCHEMA DEL CIRCUITO:
A
V ~ 50 Hz
W
V
ZR-L
DESCRIZIONE DELLA PROVA:
La prova descritta nella relazione è di tipo quantitativo, in quanto prevede l’annotazione di
dati sperimentali. Il circuito sopra riportato riproduce quello utilizzato nell’esperimento.
La tensione d’ingresso è variabile e di tipo alternato con frequenza di 50 Hz. Nel circuito
sono inseriti quattro componenti fondamentali: AMPEROMETRO e VOLTMETRO, con il
metodo a monte, per la misura della potenza apparente; WATTMETRO per la misura della
potenza attiva, e il BIPOLO PASSIVO ZR-L. La prova mira a VERIFICARE
SPERIMENTALMENTE potenza attiva e apparente assorbite dal bipolo Z R-L e di
conseguenza il suo cosφ
INSERZIONE E CARATTERISTICHE PRINCIPALI DEGLI STRUMENTI:
AMPEROMETRO: SGC ITALIA – HC18T cl 0.5 2555793 revisionato il 7/03/00
P= 2.5 A ndf= 100 KA= 0.025
VOLTMETRO:
SGC ITALIA – HC18T cl 0.5 1429336 non revisionato
P= 75 V ndf= 150 KV= 0.5 RV= 600 Ω
WATTMETRO:
SAMAR ITALIA – SL200ED cl 0.5 810626 non revisionato
PV= 150 V PA= 2 A ndf= 100 KW= 0.4 RW= 3750 Ω
L’amperometro è collegato a monte in serie alla componestisica amperometrica del
wattmetro
Ancora in serie viene collegata l’impedenza ZR-L. Il voltmetro e la componentistica
voltmetrica del wattmetro sono collegati in parallelo all’impedenza Z R-L
SVOLGIMENTO DELLA PROVA:
I dati sperimentali vengono rilevati per 5 volte,variando per ognuna di esse la tensione di
alimentazione. Per ottenere misure più accusate è consigliato utilizzare gli strumenti
nell’ultimo terzo del quadrante. I valori riportati in tabella sono stati rilevati secondo questa
indicazione.
Ad ogni variazione della tensione d’ingresso si procede alla lettura delle tacche riportato
su: amperometro, voltmetro e wattmetro. Nella tabella sono poi stati calcolati i valori
effettivi, moltiplicando il numero di tacche lette per la costante di lettura.
Le ultime due colonne della tabella sono molto importanti, in quanto rendono una misura
molto precisa della potenza attiva dissipata sul bipolo passivo; infatti all’interno del circuito
ci sono perdite di potenza attiva dovute all’inserzione dei due voltmetri, la somma di
queste due potenze viene definita AUTOCONSUMO. La potenza attiva effettiva
veramente dissipata sull’impedenza, sarà uguale alla potenza attiva misurata dal
wattmetro meno quella di autoconsumo
TABELLA DATI:
KA
nt
A
KV
nt
V
KW
nt
W
AUT
Pef f
0,025
0,025
0,025
0,025
0,025
88,5
85
81
78
74,5
2,2125
2,125
2,025
1,95
1,8625
0,5
0,5
0,5
0,5
0,5
93,5
90
86
83
80
46,75
45
43
41,5
40
0,4
0,4
0,4
0,4
0,4
150
140
128
120
110
60
56
51,2
48
44
4,2254
3,915
3,5747
3,3297
3,0933
55,7746
52,085
47,6253
44,6703
40,9067
FORMULE UTILIZZATE:
I nt K A
V nt K V
P nt KW
V2 V2
AUT
RV Rw
S V I
Peff P AUT
Q S 2 P2
cos
P
V I
Una volta rilevati i dati si potrà procedere nel calcolare il cosφ del bipolo passivo; a ogni
misurazione corrisponderà un valore più o meno uguale per tutte, in quanto l’impedenza è
sempre la stessa per ogni rilevazione. Considereremo il valore di cosφ medio.
cos
P
55.77
0.53
V I 46.75 2.21
cos
P
52.085
0.54
V I 45 2.125
cos
P
47.63
0.546
V I 43 2.205
1° mis.
2° mis.
3° mis.
cos
P
44.67
0.552
V I 41.5 1.95
cos
P
40.9
0.53
V I 40 1.863
4° mis.
5° mis.
dalle quali:
cos medio 0.53in _ ritardo
il cosφ del bipolo passivo risulta essere 0.53 e sapendo che l’impedenza è di tipo ohmico
induttiva si precisa che la corrente segue la tensione.
Il cosφ è un parametro molto importante per i blocchi passivi alimentati in regime
sinusiodale, in quanto indica la tipologia dello stesso blocco: per cosφ = 1 siamo in
presenza di un blocco puramente ohmico, per valori sempre più bassi fino a 0, si ha
invece un circuito ohmico con componenti reattive; se il cosφ = 0 il circuito è puramente
reattivo.
Il termine reattivo è pero generale, dato che esistono due tipi di reattanze:quella induttiva e
quella capacitiva.
La reattanza induttiva è fisicamente costituita da una bobina o un avvolgimento.
La reattanza capacitiva è fisicamente costituita da un condensatore.
Per intuire dal cosφ con che tipo di reattanza si ha a che fare si scrive “in anticipo” per
l’induttiva e “in ritardo” per la capacitiva. Nel primo caso la tensione anticipa la corrente,
ovvero trovandoci in regime sinusoidale si ha un continuo cambiamento di tensione da
valori positivi a valori negativi; supponiamo di avere una bobina collegata a un generatore
e manovrata da un interruttore. Come è noto dalle leggi del magnetismo una bobina
percorsa da corrente provoca un campo magnetico che per essere prodotto alla chiusura
dell’interruttore deve ricevere energia dalla tensione. In questo breve periodo di tempo la
corrente non scorre, ma inizierà a fluire quando la tensione avrà fornito abbastanza
energia da per per giungere al valore massimo del campo,sarà il successivo scorrimento
della corrente a mantenere quest’ultimo; lo stesso avverrà quando la bobina cessa di
essere alimentata e quindi il campo magnetico restituirà l’energia sotto forma di corrente.
Dato che la corrente alternata ripete ciclicamente il processo descritto sopra ci sarà
sempre l’anticipo della tensione per un’impedenza di tipo induttivo.
Diventa reciproco il discorso per la reattanza capacitiva: supponiamo di avere un
condensatore collegato a un generatore e manovrato da un interruttore. Alla chiusura di
quest’ultimo ci si trova in una situazione di corto circuito in quanto il condensatore lascia
passare corrente provocando una caduta di tensione pari a 0; in questa fase la corrente
fornisce l’energia al condensatore per formare un campo elettrico sulle sue armature, il
campo una volta giunto al suo valore massimo viene poi mantenuto dalla tensione.
All’apertura dell’interruttore l’egregia accumulata dal condensatore viene restituita dalla
tensione al generatore.
Analogamente a quanto detto prima, dato che la corrente alternata ripete ciclicamente il
processo descritto sopra ci sarà sempre il ritardo della tensione per un’impedenza di tipo
capacitivo.
Più i valori di induttanza e capacità saranno elevati, più evidenti saranno i rispettivi effetti.
In conseguenza a quanto sopra scritto, si può intuire l’unità di misura della reattanza:
l’ohm, in qunato essa rappresenta la resistenza che presentano bobine e condensatori al
passaggio della corrente alternata.
In parallelo a tutto il discorso viaggia il concetto di potenza reattiva: essa è la potenza che
il generatore scambia con il circuito per creare e ritirate ciclicamente campi elettrici (per i
condensatori) e campi magnetici (per le bobine).
La potenza reattiva non è quindi dissipativa.
qui di seguito Sono state calcolate le potenze reattive scambiate, per ogni misurazione:
2
2
2
2
1° mis Q S P 103.4 55.77 87.1 var
2
2
2
2
2° mis Q S P 95.62 5.08 80.19 var
2
2
2
2
3° mis Q S P 87.075 47.626 72.9 var
2
2
2
2
4° mis Q S P 80.92 44.67 67.47 var
2
2
2
2
5° mis Q S P 74.5 40.9 62.26 var
CONCLUSIONI:
La prova ci ha permesso di calcolare il cosφ di un bipolo passivo partendo dai dati che noi
stessi ci siamo ricavati sperimentalmente.