Distanze astronomiche
LA LEZIONE
Introduzione
La misurazione delle distanze dei corpi celesti, dalla scala galattica a quella
cosmologica, è molto importante in astronomia per conoscere la struttura della nostra
galassia e delle altre e per capire le proprietà dell’Universo. Tuttavia, mentre è
piuttosto facile misurare la distanza angolare delle stelle (Fig.1), non lo è affatto
determinare la distanza lineare. La difficoltà deriva dal fatto che nello spazio non
esistono parametri di riferimento per il confronto, come può essere per es. un righello
o un’asta per la misurazione della distanza tra due oggetti sulla Terra. Per il calcolo
delle distanze astronomiche si usano allora metodi diretti (soprattutto per gli astri più
vicini) e indiretti, ossia che sfruttano alcune
proprietà dei corpi celesti che consentono di
ricavare la loro distanza. I metodi diretti
includono tecniche geometriche, come la
parallasse.
Fig.1 Metodo empirico per valutare l'ampiezza in gradi nella volta celeste
Tenendo il braccio teso e chiudendo un occhio, il pollice copre grosso
modo un'area di 2,5°, la mano aperta 22° e le nocche del pugno chiuso
9°
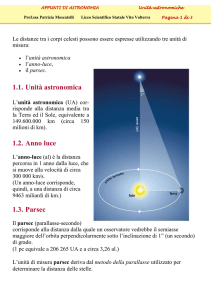
Unità di misura e valori tipici
Le principali unità di misura utilizzate per le distanze astronomiche sono l’Unità
astronomica (UA), l’anno luce e il parsec, per distanze progressivamente maggiori.
L’Unità astronomica è il metro del Sistema solare e corrisponde alla distanza media tra
il Sole e la Terra, circa 150 milioni di kilometri. L’anno luce (la locuzione può trarre in
inganno, contenendo il riferimento a un periodo temporale) si usa su scala galattica e
corrisponde alla distanza percorsa in un anno dalla luce, che nel vuoto si muove alla
velocità di circa 300.000 km/s, ossia a 9,4∙1012 km. Il parsec (parallasse di un
secondo d’arco; simbolo, pc) è usato su scala cosmica ed è la distanza di un oggetto
celeste dal quale il semiasse maggiore dell’orbita terrestre (vale a dire la distanza
massima Terra-Sole) si vedrebbe sotto l’angolo di un secondo d’arco (v. oltre):
corrisponde a 3,26 anni luce, ossia a circa trenta miliardi di kilometri.
La stella più vicina (α Centauri) dista 1,32 pc, l’ammasso stellare più vicino (Iadi) ca.
45 pc, l’ammasso globulare più vicino (M4) ca. 6000 pc, il centro galattico ca. 8500
pc, la galassia più vicina (Grande Nube di Magellano) ca. 55000 pc, l’ammasso
galattico più vicino (ammasso della Vergine) ca. 15 Mpc.
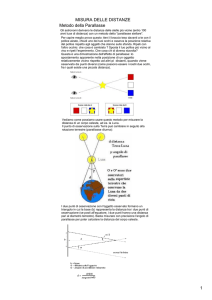
Parallasse trigonometrica
La parallasse è lo spostamento angolare apparente di un oggetto, quando viene
osservato da due punti di vista distinti. Per far comprendere meglio il concetto, è utile
descriverlo nel seguente modo: se si tende un dito davanti agli occhi e lo si guarda
alternativamente con l’occhio sinistro e con l’occhio destro, si nota che il dito sembra
spostarsi sullo sfondo, con uno scarto angolare che è funzione di quello degli occhi e
della distanza del dito. Lo stesso principio è adottato in astronomia per stimare la
distanza delle stelle più vicine, sfruttando le diverse posizioni di un osservatore che
derivano dal movimento di rotazione terrestre (parallasse diurna), di rivoluzione della
Terra attorno al Sole (parallasse annua) o di traslazione del Sistema solare rispetto a
gruppi di stelle vicine (parallasse secolare e statistica). Nota la lunghezza della base di
tali spostamenti, il passaggio dalla parallasse alla distanza è immediato se si considera
il triangolo parallattico, ossia il triangolo i cui vertici sono costituiti da un certo astro e
da due diverse posizioni di un osservatore. Il vantaggio della parallasse è che si tratta
di un metodo puramente geometrico, che non necessita di ipotesi sugli oggetti celesti
dei quali si vuole misurare la distanza.
Parallasse diurna
Un osservatore O sulla superficie terrestre vede sulla volta celeste c un corpo celeste
A in una posizione At (posizione topocentrica) diversa da quella, Ac (posizione
geocentrica), in cui lo vedrebbe un osservatore ideale situato nel centro G della Terra
(Fig.2).
Conseguentemente, la distanza zenitale (distanza angolare
tra lo zenit dell’osservatore e il corpo celeste) di A
misurata da O, z0, è di poco maggiore della distanza
zenitale z misurata da un osservatore fittizio posto in G
che assumesse come direzione dell’asse zenitale la stessa
dell’osservatore in O (cioè la direzione GO). La distanza
angolare p tra la posizione geocentrica e quella
Fig.2 Parallasse diurna
topocentrica è la parallasse diurna, o semplicemente parallasse, del corpo celeste.
Naturalmente, p è anche l’angolo sotto cui dal corpo celeste viene visto il raggio
terrestre condotto al luogo d’osservazione, GO. Facendo riferimento alla Fig.2,
considerazioni di carattere trigonometrico a un livello matematico avanzato (che
possono anche essere omesse) permettono di ricavare la distanza del corpo celeste.
Infatti, applicando il teorema dei seni al triangolo GOA, si ha che senp=(R/r)senz, da
cui p(R/r)senz (essendo senpp, in radianti, poiché gli angoli di parallasse sono
generalmente molto piccoli), dove R è il raggio terrestre nel luogo d’osservazione, r la
distanza geocentrica, GA, del corpo celeste e z la sua distanza zenitale vera, cioè
geocentrica.
La parallasse diurna di un corpo celeste può essere valutata effettuando l’osservazione
del corpo in uno stesso istante da parte di due osservatori terrestri distanti oppure da
parte di uno stesso osservatore in tempi successivi, quando per effetto della rotazione
terrestre la direzione della visuale è variata sufficientemente. Soltanto all’interno del
Sistema solare tale parallasse è diversa da zero e quindi tale metodo di calcolo delle
distanze è utilizzabile; per distanze maggiori la direzione di osservazione di un corpo
celeste è praticamente la stessa da qualunque posizione della superficie terrestre (vale
a dire la base del triangolo parallattico è trascurabile rispetto alla distanza delle stelle)
e per ottenere un angolo di parallasse bisogna ricorrere al movimento di rivoluzione
della Terra attorno al Sole. La Luna ha parallasse diurna di circa 5702, il Sole di
8,794, Plutone di 0,25, mentre Proxima Centauri (la stella più vicina) di 0,00002
(non misurabile).
Il calcolo della distanza dei pianeti del Sistema solare si ottiene con più precisione
usando la tecnica del radar: se Δt è l'intervallo di tempo trascorso fra l'istante in cui
viene inviato l'impulso di onde radio e quello in cui viene ricevuto il segnale riflesso dal
pianeta, si ha che dp=(1/2)cΔt, dove c è la velocità della luce.
Parallasse annua
Se si assume per semplicità che la Terra compia
un’orbita circolare attorno al Sole di raggio uguale alla
distanza media u, un osservatore terrestre vede sulla
volta celeste c una stella A in una posizione Ag
(posizione geocentrica) diversa da quella, Ae (posizione
eliocentrica), in cui la vedrebbe un osservatore ideale
situato sul Sole S (Fig.3). Nel corso dell’anno varia il
Fig.3 Parallasse annua e trattazione trigonometrica
punto di vista geocentrico e varia quindi Ag: a questo apparente moto periodico annuo
di una stella si dà il nome di parallasse annua e l’orbita della stella a distanza r dalla
Terra sarà (nell’approssimazione iniziale fatta) una circonferenza di raggio u, su un
piano parallelo al piano dell’eclittica, a distanza r da quest’ultimo. Considerando il
triangolo parallattico STA, si ha che u=rtanprp (essendo tanpp, in radianti, poiché
gli angoli di parallasse sono molto piccoli). Poiché un radiante equivale a 206.625
secondi d’arco, si ottiene che r=(206.625 u)/p, dove p indica l’angolo di parallasse
misurato in secondi d’arco.
Questa trattazione avanzata della parallasse annua
mediante l’uso di sistemi trigonometrici può
eventualmente omessa in favore di un approccio più
elementare che fa riferimento alla Fig.3a, dove R è la
distanza tra la Terra (T) e il Sole (S), considerata
costante, p l’angolo di parallasse misurato in secondi
d’arco e d la distanza della stella. In virtù della distanza
molto grande della stella, R può essere approssimata
con l’arco della circonferenza centrata sulla stella, di
raggio d. Poiché 360°=(3606060), si ha la
Fig.3a Parallasse annua: una trattazione semplificata
proporzione R : 2d = p : (3606060), da cui si ricava che d=R(3606060)/(p2).
Poiché R = 1 UA e 3606060/2 = costante = 206.625, se definiamo 1 pc = 206.625,
la precedente relazione, espressa in parsec, diventa d=1/p, cioè la distanza e la
parallasse sono inversamente proporzionali.
Malgrado questa formula per la determinazione delle distanze mediante la parallasse
sia concettualmente molto semplice, il calcolo effettivo è particolarmente elaborato e
richiede molta accuratezza nelle osservazioni. Generalmente si osserva lo stesso corpo
celeste a sei mesi di distanza (quando la Terra viene a trovarsi in due punti opposti
della sua orbita) e si analizza lo spostamento apparente del corpo; dagli spostamenti
si ricavano gli angoli di parallasse e quindi le distanze. La prima stella di cui si è
misurata la parallasse è stata 61 Cygni, della quale nel 1806 Giovanni Piazzi stimò un
valore di 0,3, che corrisponde a una distanza di 10 anni luce.
Per effetto della rivoluzione della Terra attorno al Sole
cambia la direzione di osservazione di una stella e
quest’ultima appare descrivere in un anno una piccola
ellisse (ellisse di parallasse o parallattica) sul piano
tangente alla sfera celeste il cui centro è Ae (Fig.4), tanto
più piccola quanto più lontano è l’astro. Ancora con una
trattazione avanzata trigonometrica, il semiasse
Fig.4 Ellisse di parallasse annua sulla sfera celeste
maggiore dell’ellisse a, parallelo al piano dell’eclittica, è visto sotto un angolo pu/r
radianti, mentre il semiasse minore è visto sotto un angolo pari a psenl, essendo l la
latitudine celeste dell’astro (nella Fig.4, e è l’eclittica ed E il polo dell’eclittica); il
centro Ae dell’ellisse di parallasse corrisponde alla posizione eliocentrica della stella
sulla volta celeste.
Alla luce delle precedenti considerazioni si ricava subito che la distanza in
corrispondenza della quale l’angolo di parallasse è pari a 1 risulta essere d(1) = 1 UA
206.625/1 = 3,0861019 km; questa lunghezza prende il nome di parsec (pc). Le
parallassi delle stelle sono minori di 1 (Proxima Centauri ha parallasse annua di
0,76, Sirio di 0,37 mentre 61 Cygni di 0,30) e oltre 300 pc non si può stimare la
loro distanza con metodi geometrici. Si utilizzano allora metodi indiretti (v. oltre).
Parallasse secolare
In questo caso si usa come base per la misura dell’angolo di parallasse il tratto del
moto proprio del Sole nella Galassia. Il Sole si
muove con una velocità di circa 20 km/s, rispetto
alle stelle vicine, in una direzione nota come apice
solare; esso pertanto percorre circa 4,1 UA in un
anno (corrispondenti a una velocità di 19 km/s).
Se indichiamo con s lo spostamento del Sole in un
dato numero di anni, nel triangolo S1S2A (Fig.5),
che ha per vertici la posizione iniziale (S1) e finale
(S2) del Sole e quella della stella (A), si conoscono
il lato S1S2=s, l'angolo formato dalla direzione
dell'apice solare a con quella della stella e l'angolo
u che misura lo spostamento angolare della stella
durante l'intervallo di tempo considerato.
Fig.5 Parallasse secolare
Applicando a tale triangolo il teorema dei seni, si ricava la distanza della stella, ossia
dA=s sen/senusen/u (in quanto, come al solito, u è molto piccolo). Tale
procedimento non è applicabile a una singola stella, in quanto questa è, a sua volta, in
moto con una certa velocità (la sua velocità peculiare). Tuttavia, dato che le velocità
peculiari sono distribuite a caso, se si considera un gruppo di stelle vicine è possibile
eliminare questa causa di errore mediando i loro moti propri. Si ottiene così la
distanza media del gruppo di stelle. Il metodo della parallasse secolare (o statistica) è
applicabile fino a distanze di circa 500 pc.
Distanze extragalattiche
Per la determinazione delle distanze extragalattiche si fa uso di metodi che fanno
riferimento ai cosiddetti indicatori di distanza (o candele standard), ossia oggetti
celesti di cui è nota la luminosità assoluta (ossia quella intrinseca, effettivamente
emessa dall’astro) in base a qualche loro proprietà, per i quali quindi si può ottenere
una misura affidabile della loro distanza a partire dalla luminosità apparente (quella
osservata al telescopio). Queste tre grandezze sono infatti legate tra loro e
conoscendone due si ricava la terza. In generale, la luce emessa da un corpo celeste
diminuisce con il quadrato della distanza: per confrontare la luminosità di stelle
diverse dovremmo considerarle tutte poste alla stessa distanza. Se così fosse, il cielo
stellato ci apparirebbe molto diverso da quello che conosciamo: il Sole diventerebbe
una delle tante stelle deboli che brillano in cielo, molte altre stelle luminose si
indebolirebbero, mentre stelle invisibili diventerebbero splendenti.
Gli indicatori di distanza primari devono essere calibrati mediante osservazioni
effettuate nella nostra galassia oppure attraverso considerazioni di tipo teorico. Una
volta stabilite la distanze delle galassie più vicine, queste possono essere utilizzate per
calibrare gli indicatori di distanza secondari.
Per distanze ancora maggiori si fa uso della legge di Hubble, in base alla quale le
galassie si allontanano le une dalle altre con una velocità che è direttamente
proporzionale alla loro distanza, secondo la relazione v=H0d, dove H0 è la costante di
Hubble, un parametro il cui valore stimato è continuamente raffinato mediante
misurazioni sempre più accurate di distanze e velocità di un gran numero di galassie,
che attualmente vale 70,8±1,6 km/(s·Mpc). Questo metodo dipende dal modello
teorico utilizzato per
descrivere
l’espansione
dell’Universo.
La Fig.6 illustra la
scala di applicazione
delle principali
tecniche utilizzate
per determinare le
distanze delle stelle
e delle galassie.
Fig.6 Scala di distanze astronomiche e relative metodi di misurazione. Le distanze sono espresse in anni luce (Light-Years) e sono
indicate per confronto alcune tipiche stelle e galassie. Il redshift (spostamento verso il rosso) è un effetto che deriva dalla legge di
Hubble, chelega in modo proporzionale la velocità di allontanamento delle galassie alla loro distanza
Indicatori primari
I principali indicatori di questo tipo sono le stelle Cefeidi e RR Lyrae (utilizzabili fino a
distanze di 4 Mpc), e le supernovae di tipo Ia (utilizzabili fino a distanze di 100 Mpc).
Le Cefeidi e le RR Lyrae sono stelle variabili la cui pulsazione varia con il tempo con un
periodo che è proporzionale alla luminosità assoluta: quest’ultima si ricava quindi
misurando tale periodo e, confrontata con la
luminosità apparente, fornisce la distanza. Il
periodo di variabilità di una stella è
relativamente facile da calcolare e le Cefeidi
in particolare (la cui pulsazione è causata da
un periodico movimento di espansione e
contrazione dell’astro) sono facilmente
individuabili perché più brillanti rispetto alle
RR Lyrae. La luminosità di queste ultime
varia con regolarità su periodi che vanno da
qualche ora a più di un giorno, mentre per le
Cefeidi i periodi vanno da 1 a circa 50 giorni
(Fig.7).
Fig.7 Relazione periodo luminosità per le Cefeidi della Via Lattea e della Grande Nube di Magellano. La luminosità è espressa in
magnitudini mentre il periodo di variabilità in giorni. Il diagramma è stato costruito sulla base dei dati raccolti dal telescopio
spaziale Spitzer
La misura della parallasse trigonometrica di certo numero di Cefeidi all’interno della
nostra galassia ha consentito di ottenere un'accurata calibrazione della relazione
periodo-luminosità, che applicata alle Cefeidi osservate dal telescopio spaziale Hubble
in galassie più lontane ha permesso di
stimare distanze dell’ordine di 107 pc.
Per la determinazione corretta delle
distanze il metodo si utilizza nel seguente
modo: si costruisce la relazione periodoluminosità assoluta di un certo numero di
Cefeidi situate al di fuori della Via Lattea e
si confronta con la medesima relazione che
si ottiene prendendo in considerazione le
Cefeidi contenute nella nostra galassia la
cui distanza è nota perché calcolata con
altri metodi. Eventuali errori di calibrazione
si propagano in modo sistematico sulle
misure di distanze successive.
Le supernovae di tipo Ia sono fenomeni
esplosivi associati a nane bianche (stelle
collassate in uno stato di alta densità) che
catturano materia da stelle compagne di un
sistema binario fino a un limite massimo
che porta al collasso (Fig. 8).
Fig.8 Illustrazione dei fenomeni stellari esplosivi noti come supernovae di tipo Ia. La nana bianca di un sistema binario riceve massa
dalla stella compagna fino a superare il limite di accumulazione e quindi a esplodere
Il picco di luminosità raggiunto nell’esplosione (paragonabile a quello di una tipica
galassia, quindi osservabile anche a grandi distanze) è lo stesso per ogni supernova di
questo tipo, in virtù del fatto che le nane bianche hanno tutte la stessa massa, ed è
quindi noto a priori: ancora una volta, conoscendo questa luminosità assoluta e
misurando quella apparente si risale alla distanza.
Anche le novae sono fenomeni esplosivi probabilmente legati alla presenza di stelle
nane in sistemi binari, che mostrano un improvviso aumento di luminosità seguito da
un abbassamento molto lento, che può durare anche alcuni anni. La luminosità
massima raggiunta durante le esplosioni è tuttavia un milione di volte minore rispetto
a quella delle supernovae.
Indicatori secondari
Tra gli indicatori di questo tipo rientrano le stelle supergiganti rosse, che osservate in
diverse galassie di distanza nota hanno mostrato la stessa luminosità assoluta, così da
poter essere utilizzate come candele standard. Anche le più brillanti nubi di idrogeno
ionizzato (le cosiddette regioni HII) possono servire per ricavare la distanza delle
galassie in cui sono contenute, dal momento che sembrano avere dimensioni legate
alla luminosità della galassie stesse. La luminosità degli ammassi globulari (ammassi
di stelle molto vecchie caratterizzati da una simmetria approssimativamente sferica,
con un addensamento centrale) segue la stessa distribuzione in tutte le galassie, per
cui dalla loro luminosità apparente si può ricavare la distanza delle galassie che li
contengono.
Una classe interessante di indicatori di distanza è costituita dalle binarie a eclisse,
coppie di stelle rare che orbitano attorno al comune baricentro passando regolarmente
una davanti all’altra.
Quando ciò accade, la luminosità totale
osservata diminuisce, sia quando la
prima stella passa davanti alla seconda
sia, per una diversa quantità, quando
passa dietro (Video). Lo studio accurato
di queste variazioni di luminosità e la
misurazione della velocità orbitale delle
stelle consente di calcolare le dimensioni
delle componenti il sistema, le loro
masse e altri parametri delle loro orbite,
informazioni che combinate con
misurazioni precise della luminosità
totale e dei colori delle stelle
permettono di determinarne le distanze in modo notevolmente accurato. Questo
metodo è stato recentemente utilizzato per determinare con una maggiore precisione
la distanza della Grande Nube di Magellano, la galassia più vicina alla nostra, che è
risultata essere di 163.000 anni luce, con un errore di circa il 2%.