A02
Giovanni Battista Bachelet
Vito Domenico Pietro Servedio
Elementi di fisica atomica
molecolare e dei solidi
II edizione
Aracne editrice
www.aracneeditrice.it
[email protected]
Copyright © MMXVII
Gioacchino Onorati editore S.r.l. – unipersonale
www.gioacchinoonoratieditore.it
[email protected]
via Vittorio Veneto, 20
00020 Canterano (RM)
(06) 45551463
ISBN
978-88-548-9894-3
I diritti di traduzione, di memorizzazione elettronica,
di riproduzione e di adattamento anche parziale,
con qualsiasi mezzo, sono riservati per tutti i Paesi.
Non sono assolutamente consentite le fotocopie
senza il permesso scritto dell’Editore.
I edizione: marzo 2017
Indice
7
Introduzione
11
Capitolo I
Fisica atomica
1.1. Gli spettri atomici, 11 – 1.1.1. Da Fraunhofer a Bunsen e Kirchhoff, 12 –
1.1.2. Il reticolo di diffrazione, 14 – 1.1.3. Lo spettro dell’idrogeno, 17 – 1.1.4. Elementi alcalini, uno spettro diverso dall’idrogeno, 18 – 1.2. Richiami di elettromagnetismo, meccanica classica e meccanica quantistica, 20 – 1.2.1. Unità
elettrostatiche e potenziale vettore, 20 – 1.2.2. Gauge trasversa ed equazione delle
onde, 21 – 1.2.3. Onda piana monocromatica, 22 – 1.2.4. Elettrone e nucleo
in campo elettromagnetico, 23 – 1.2.5. Hamiltoniana quantistica imperturbata,
unità atomiche, 24 – 1.2.6. Perturbazioni periodiche nel tempo, 26 – 1.3. Interpretazione dello spettro dell’idrogeno, 27 – 1.3.1. Assorbimento e emissione,
probabilità di transizione, 29 – 1.3.2. Regola d’oro di Fermi, 33 – 1.3.3. Assorbimento ed emissione stimolata, 34 – 1.3.4. Approssimazione di dipolo e regole di
selezione, 36 – 1.3.5. Emissione spontanea, 42 – 1.3.6. Coefficienti di Einstein, 43
– 1.3.7. La riga piú intensa dell’atomo di idrogeno, 47 – 1.4. Dall’idrogeno
alla Tavola Periodica, 48 – 1.4.1. Proprietà periodiche degli elementi: la valenza, 49 – 1.4.2. Orbitali, principio di Pauli, core e valenza, 50 – 1.4.3. Energie e
raggi atomici: trend sorprendenti, 52 – 1.4.4. Elettroni interagenti, campo elettrostatico medio, 55 – 1.4.5. Rimozione della degenerazione coulombiana, 62 –
1.4.6. Idrogeno e alcalini: conclusioni e avvertenze, 64.
67
Capitolo II
Fisica molecolare
2.1. Lo ione molecolare H+2 , prototipo delle molecole biatomiche omonucleari, 68 – 2.1.1. Approssimazione di Born e Oppenheimer, 69 – 2.1.2. Vibrazioni e
rotazioni nucleari, 73 – 2.1.3. Approssimazione armonica, 76 – 2.1.4. Approssimazione di rotatore rigido, 77 – 2.1.5. Livelli energetici roto–vibrazionali, 78
– 2.2. H2+ e molecole omonucleari, 80 – 2.2.1. Approssimazione LCAO, 80
– 2.2.2. Uso della simmetria, 82 – 2.2.3. Valor medio dell’hamiltoniana, 83 –
2.2.4. Stato legante e antilegante, 86 – 2.2.5. Base né ortogonale, né completa?, 89
– 2.2.6. Completezza e ortonormalità nello spazio vettoriale euclideo a tre dimensioni, 91
– 2.2.7. Spazio di Hilbert: infinite dimensioni, 92 – 2.2.8. Sottospazi a dimensione
finita: l’esempio di H+2 , 93 – 2.2.9. Principio variazionale associato all’equazione
di Schrödinger, 94 – 2.2.10. Base finita, equazione secolare, 95 – 2.2.11. Due funzioni di base: problema secolare 2 × 2, 96 – 2.3. Modello di molecola biatomica
eteronucleare, 97 – 2.4. Molecole biatomiche con piú di un elettrone: l’esempio
di Na2 , 101 – 2.5. Molecole poliatomiche cicliche: simmetrie e legame con i
solidi, 106 – 2.5.1. Rivisitazione del dimero omonucleare, 106 – 2.5.2. Modello di
trimero omonucleare, 108 – 2.5.3. Catena di N atomi chiusa su se stessa, 112 –
2.5.4. Una molecola poliatomica: il benzene C6 H6 , 115.
5
6
Indice
123
Capitolo III
Fisica dei solidi
3.1. Tight binding a primi vicini, 124 – 3.1.1. Catena lineare infinita, 124
– 3.1.2. Reticolo quadrato e cubico semplice, 128 – 3.2. Densità degli stati,
energia di Fermi, superficie di Fermi, 131 – 3.2.1. Densità degli stati, 131
– 3.2.2. Numero degli stati e livello di Fermi, 132 – 3.2.3. Densità degli stati e
livello di Fermi nel tight binding a primi vicini, 133 – 3.2.4. Livello di Fermi e
superficie di Fermi, 135 – 3.3. Elettrone libero: la conduzione da Drude a
Sommerfeld, 140 – 3.3.1. Teoria di Drude, 141 – 3.3.2. Teoria di Sommerfeld, 144
– 3.3.3. Calore specifico per un metallo di elettroni liberi, 147 – 3.3.4. Conduzione
elettrica in un metallo di elettroni liberi, 151 – 3.4. Cristalli, reticolo diretto
e reciproco, 157 – 3.4.1. Reticolo e cella primitiva, 158 – 3.4.2. Base, 160 –
3.4.3. Reticolo reciproco e prima zona di Brillouin, 161 – 3.5. Teorema di Bloch
e bande di energia, metalli e isolanti, 162 – 3.5.1. Funzioni di Bloch, 165
– 3.5.2. Base di onde piane, 166 – 3.5.3. Elettrone libero, ripiegamento delle
bande, 167 – 3.5.4. Elettrone quasi libero, gap, 169 – 3.5.5. Metalli e isolanti, 170
– 3.5.6. Resistenza in funzione della temperatura, 176 – 3.5.7. Conclusioni, 178.
179
Bibliografia
182
Elenco delle figure
Introduzione
Quando eravamo studenti di Fisica, la laurea era quadriennale e il corso
di Struttura della Materia, al terzo anno, copriva tutta la fisica atomica,
molecolare e dei solidi che un laureato di allora era tenuto a sapere. L’esame era fra i piú pesanti del terzo anno: parecchi non lo superavano al
primo colpo e alcuni nemmeno al secondo. Il programma, smisurato ed
eterogeneo, consisteva in una minuziosa collezione di esperimenti storici la
cui interpretazione, in mancanza di concetti e strumenti appropriati (come
la teoria quantistica relativistica o i metodi di campo medio, inaccessibili a
uno studente del terzo anno), era quella dei primi del Novecento, quando
il nuovo quadro teorico era in costruzione ed erano inevitabili approcci semiempirici e regolette ad hoc. C’era cosí il rischio di perdersi in un labirinto
di regole di selezione con o senza campo magnetico, modellini vettoriali
classici per momenti angolari quantistici, difetti quantici, cariche efficaci,
singoletti e tripletti, scanditi da una litania di nomi illustri: Hund e Pauli,
Hartree e Fock, Heitler e London, Zeeman o Paschen e Back. Non sempre
si capiva quali e quante approssimazioni fossero di volta in volta adottate;
raramente emergeva con chiarezza il punto principale dell’esperimento
o della sempre diversa regola necessaria a comprenderlo. Nella mente
dello studente, a consuntivo, rimanevano impresse (però come un incubo)
antiquate tecniche interpretative di complessi spettri atomici o molecolari,
mentre sul legame chimico, la corrente elettrica o i trend della Tavola Periodica la nebbia era ancora fitta. Anche nell’ultima parte di corso, infatti,
la maratona fra esperimenti e modelli non andava al cuore dei principali
fenomeni nei solidi: arrivato agli scritti, lo studente si trovava spesso a
domandarsi, frastornato, quale dei tanti modelli visti nel corso si applicasse
al suo particolare esercizio, con scarsa intuizione della fisica sottostante.
Nei primi anni del 2000, quando per effetto del processo di Bologna1
anche la laurea in Fisica si è trasformata in triennale+magistrale, alla
Sapienza abbiamo spezzato il vecchio corso di Struttura in due tronconi
1. Che ha armonizzato titoli e percorsi di studio, dando ulteriore impulso alla mobilità degli
studenti nell’Unione Europea, vedi http://it.wikipedia.org/wiki/Processo_di_Bologna.
7
8
Introduzione
meno pesanti e piú abbordabili (uno al terzo anno della laurea triennale
e uno al primo della laurea magistrale) ripensando anche il programma.
Lo sdoppiamento non doveva essere una banale ripartizione di ore,
crediti e argomenti in due blocchi (fisica atomica e molecolare alla triennale, fisica dei solidi alla magistrale), ma l’occasione per una riforma
radicale del precedente impianto. Ambedue i corsi avrebbero avuto
per oggetto atomi, molecole e solidi. Sembrava infatti curioso che un
laureato triennale in Fisica dovesse avere qualche idea elementare sul
decadimento delle particelle e non, ad esempio, su ciò che rende un
isolante diverso da un conduttore, uno dei successi decisivi della meccanica quantistica. La differenza fra il corso della triennale e quello della
magistrale sarebbe stata nel livello e nell’ampiezza della trattazione. Il
corso di base della laurea triennale, con il vecchio nome di “Struttura
della Materia”, si sarebbe mantenuto a livello elementare e limitato nel
contenuto. Il corso avanzato della laurea magistrale, con il nome di
“Fisica della Materia Condensata”, avrebbe approfondito e ampliato la
trattazione in modo da ricuperare il contenuto essenziale del corso di
Struttura della laurea quadriennale, alleggerito delle parti obsolete.
Questo libro nasce dalle lezioni di uno dei primi corsi di Struttura
della Materia di questo tipo, tenuto a Fisica dagli autori nel 2007-2008.
Affronta perciò in modo elementare un limitato numero di fenomeni
della fisica atomica, molecolare e dei solidi, sulla base di concetti e
strumenti teorici accessibili a chi abbia seguito i corsi di Metodi Matematici della Fisica, Meccanica Quantistica e Meccanica Statistica2 . Si
parte dall’esistenza stessa di un atomo stabile e dall’assorbimento ed
emissione della luce da parte di atomi semplici, per arrivare a lambire
la natura metallica o isolante dei solidi, passando per la straordinaria regolarità della Tavola Periodica e la formazione delle molecole.
Ognuna di queste tappe corrisponde ad uno dei successi che nei primi
2. A proposito di prerequisiti, nel libro, come avvenuto nel corso, vengono richiamati con
qualche dettaglio due strumenti della meccanica quantistica, la teoria delle perturbazioni dipendenti dal tempo e quella delle approssimazioni variazionali, non esclusivi della Struttura della
Materia, ma necessari, nel curriculum di Fisica alla Sapienza, in quanto non discussi a fondo in
nessun altro corso obbligatorio. Sempre a proposito di prerequisiti, è utile sottolineare che in questo libro vengono forniti abbondanti e puntuali riferimenti alla bibliografia (oltre a molti link,
particolarmente utili a chi si avvale della versione elettronica e/o non ha quei libri a casa). L’insieme di questi riferimenti è tale da consentire non solo di ricostruire i prerequisiti eventualmente
mancanti o zoppicanti, ma anche, a chi lo voglia, di approfondire oltre il livello dei vecchi corsi di
Struttura della Materia la molta fisica atomica, molecolare e dei solidi che resta fatalmente fuori
da questa trattazione introduttiva.
Introduzione
9
trent’anni del secolo scorso hanno accompagnato la nascita e il trionfo
della meccanica quantistica. In questo modo il libro seleziona e fornisce
un primo sguardo alla fisica della materia, secondo un percorso breve
e originale: escluse le ore dedicate alle esercitazioni, le lezioni hanno
occupato in tutto trenta ore: dieci per gli atomi, dieci per le molecole
e dieci per i solidi, corrispondenti ai capitoli di questo libro, che può
rappresentare uno strumento utile anche per docenti e studenti dei
corsi di laurea triennale in Chimica o Ingegneria dei Materiali.
Roma, novembre 2014
Grazie alla vivace partecipazione degli studenti del corso di Struttura
della Materia tenuto alla Sapienza nella primavera 2016 (in particolare
di F. Miceli, G. Perrupato, L. Sarra, S. Soltani, L. Talamanca, A. Testa)
sono emerse sviste e passaggi poco chiari (sull’approssimazione di
Born-Oppenheimer, ad esempio) che hanno suggerito l’opportunità di
questa seconda edizione riveduta e corretta.
Roma, novembre 2016
Capitolo I
Fisica atomica
1.1. Gli spettri atomici
Fra la fine del XIX secolo e l’inizio del XX i fisici raggiunsero, con
Thomson, la certezza che la materia sia composta di elettroni carichi
negativamente1 e di nuclei carichi positivamente, migliaia di volte piú
pesanti degli elettroni2 . La scoperta del nucleo demolí il modello di
atomo proposto pochi anni prima proprio da Thomson (un panettone
omogeneo positivo con dentro gli elettroni distribuiti come le uvette), e
suggerí a Rutherford un altro modello, di tipo planetario, nel quale il
nucleo positivo occupa la posizione del sole e gli elettroni giocano il
ruolo dei pianeti. Questo nuovo modello poneva, però, piú problemi di
quanti ne risolvesse, perché entrava in conflitto con l’elettrodinamica
classica [1]. In quegli stessi anni a cavallo fra Ottocento e Novecento
era stato infatti dimostrato3 , a partire dalle equazioni di Maxwell4 , che
una carica accelerata emette radiazione elettromagnetica. Un sistema
planetario basato sull’attrazione elettrostatica (anziché su quella gravitazionale) non poteva, quindi, essere stabile: gli elettroni, orbitando
intorno al nucleo, avrebbero emesso radiazione, perdendo rapidamente energia e precipitandoci sopra. Come mai gli elettroni non cadano
sul nucleo e gli atomi, mattoni dell’universo (dalle molecole dei gas
alla materia vivente), siano quindi stabili, è una delle domande che
trovò risposta solo nella meccanica quantistica [2]; un’altra domanda,
non meno importante, riguardava gli spettri atomici e la loro natura
1. Per l’esperimento dei raggi catodici, fatto nel 1897, Thomson vinse il Nobel per la Fisica
nel 1906 http://en.wikipedia.org/wiki/J._J._Thomson#Discovery_of_the_electron.
2. Lo scoprirono Geiger e Marsden nel 1909, bombardando con particelle α un sottile foglio
d’oro nel laboratorio diretto da Rutherford, Nobel per la Chimica 1908 per le sue scoperte sul
legame fra radioattività e disintegrazione degli atomi http://en.wikipedia.org/wiki/Ernest_
Rutherford#Rutherford_and_the_Gold_Foil_Experiment.
3. https://it.wikipedia.org/wiki/Potenziale_di_Lienard-Wiechert#Equazione_di_Larmor.
4. http://it.wikipedia.org/wiki/Equazioni_di_Maxwell.
11
12
Elementi di fisica atomica, molecolare e dei solidi
discreta, su cui nell’Ottocento si era accumulata una grossa mole di dati
sperimentali.
Newton aveva studiato la luce solare facendola passare attraverso
un prisma5 e osservando, per la prima volta con occhio di scienziato,
l’arcobaleno di colori che passano dal rosso al violetto con continuità.
Solo ai primi dell’Ottocento, però, si cominciò a osservare che questa distribuzione di colori non è davvero continua: presenta, invece, qualche
isolato, sottile intervallo di oscurità. Per meglio comprendere lo spettro
del sole si svilupparono allora strumenti sempre piú accurati nella decomposizione della radiazione luminosa; si cominciò anche a studiare
lo spettro luminoso di gas portati artificialmente all’incandescenza,
scoprendo che, molto diversamente dal sole, in questi spettri compaiono soltanto alcune righe colorate, e tutto il resto è nero. Studiando la
particolare posizione di queste righe nello spettro luminoso si scoprí
poi che ad ogni elemento chimico corrisponde una diversa sequenza
di righe (linee spettrali): una specie di impronta digitale dell’elemento.
La spettroscopia assurse insomma al ruolo di scienza, e il suo grande
sviluppo contribuí alla nascita della meccanica quantistica non meno
degli esperimenti sull’esistenza e la natura dell’elettrone e del nucleo.
In questo capitolo ripercorreremo le tappe di questo sviluppo e
richiameremo le nozioni di fisica classica e quantistica necessarie alla
descrizione dell’interazione fra luce e materia, per giungere infine ad
una prima, elementare comprensione degli stati elettronici nell’atomo e
della struttura della Tavola Periodica degli elementi.
1.1.1. Da Fraunhofer a Bunsen e Kirchhoff
Il primo ad osservare zone scure nello spettro del sole fu il chimico
inglese William Hyde Wollaston6 nel 1802. L’inizio di esperimenti quantitativi coinvolgenti la misurazione della lunghezza d’onda della luce
si deve a Joseph von Fraunhofer7 in quanto inventore, nel 1821, del
reticolo di diffrazione.
5. Come abbiamo appreso nel primo biennio di Fisica, il prisma scompone la luce nelle sue
componenti in virtú della dipendenza dell’indice di rifrazione del materiale dalla lunghezza
d’onda della radiazione elettromagnetica incidente; in ottica geometrica, il rapporto tra il seno
dell’angolo incidente e di quello rifratto è pari al reciproco del rapporto tra gli indici di rifrazione
dei mezzi corrispondenti.
6. http://it.wikipedia.org/wiki/William_Hyde_Wollaston.
7. http://it.wikipedia.org/wiki/JosephvonFraunhofer.
I.
Fisica atomica
13
Figura 1.1. Linee di Fraunhofer (vedi testo).
Già nel 1814 però, sette anni prima di inventare il reticolo di diffrazione, Fraunhofer, usando un semplice prisma, riscoprí indipendentemente da Wollaston le linee scure dello spettro solare e cominciò una
classificazione sistematica. Catalogò in tutto 570 linee, assegnando alle
principali le lettere da A a K e altre lettere alle linee piú deboli (vedi
Fig. 1.1). Tali righe sono ancora oggi chiamate linee di Fraunhofer8
in suo onore. Fu inoltre il primo a notare che gli spettri di Sirio e di
altre stelle brillanti erano diversi tra loro e da quello del Sole, dando
inizio alla spettroscopia stellare. L’applicazione sistematica dell’analisi spettrale alla chimica cominciò però in Pennsylvania, quando nel
1854 il medico David Alter9 pubblicò l’articolo “On Certain Physical
Properties of Light Produced by the Combustion of Different Metals in
an Electric Spark Refracted by a Prism”, presentando una tabella con
le linee colorate relative a dodici elementi e dimostrando che le linee
spettrali dell’ottone corrispondevano a quelle di rame e zinco. Sei mesi
piú tardi ampliò il suo lavoro analizzando lo spettro di sei gas e rivelando, fra l’altro, l’allora sconosciuta “serie di Balmer” dell’idrogeno.
Parallelamente ad Alter, in un documento presentato nel 1853 all’accademia reale delle scienze svedese, il fisico Anders Jonas Ångström10
presentava una ricerca sulle linee spettrali dei gas, nella quale fra l’altro
postulava che un gas incandescente emetta raggi luminosi alla stessa
“refrangibilità” (frequenza) dei raggi che assorbe.
Infine nel 1860 un chimico e un fisico tedeschi, Robert Bunsen11
e Gustav Kirchhoff12 , ampliando le scoperte di Alter ed Ångström,
8.
9.
10.
11.
12.
http://it.wikipedia.org/wiki/Linee_di_Fraunhofer.
http://it.wikipedia.org/wiki/David_Alter.
http://it.wikipedia.org/wiki/Anders_Jonas_Ångström.
http://it.wikipedia.org/wiki/Robert_Bunsen.
http://it.wikipedia.org/wiki/Gustav_Kirchhoff.
14
Elementi di fisica atomica, molecolare e dei solidi
confermarono che a ciascun elemento chimico può essere associata una
serie di righe spettrali, e ne dedussero che le linee scure nello spettro
solare fossero dovute all’assorbimento da parte degli elementi presenti
negli strati piú esterni del sole.
Tali scoperte furono realizzate nel 1861 da Bunsen e Kirchhoff per
mezzo di un dispositivo ideato l’anno precedente (vedi Fig. 1.2), che metteva insieme un “becco Bunsen”, bruciatore a gas con il quale è possibile
raggiungere i 1400 gradi Celsius, ed uno “spettroscopio di Kirchhoff”,
strumento ottico accoppiato a un prisma. La combustione dei vapori originati dal comune sale da cucina (cloruro di sodio), produceva una riga
gialla luminosa alla stessa frequenza della riga (scura) D di Fraunhofer,
che fu attribuita al sodio. Tentando poi di sovrapporre la radiazione dei
vapori di sodio a quella del sole in modo da cancellare la riga scura D
dallo spettro solare, i due scoprirono che, anziché scomparire, la riga
scura D (e con lei le altre righe scure corrispondenti a quelle luminose
del sodio) diventava ancora più scura. Molto interessante anche la loro
scoperta di due nuovi elementi chimici, denominati rubidio e cesio in
relazione al colore delle loro linee spettrali piú intense (in latino caesius
significa grigio–azzurro e rubidus rosso cupo) nella regione della luce
visibile, grazie all’analisi dei residui della evaporazione di 44mila (!) litri
di acqua minerale attinta alle sorgenti di Bad Dürkheimer.
Il lavoro di Bunsen e Kirchhoff culminò con la stesura delle tre leggi
di Kirchhoff della spettroscopia:
a) un solido incandescente produce una luce con spettro continuo;
b) un gas rarefatto incandescente produce luce composta da linee
spettrali a lunghezze d’onda discrete;
c) un solido incandescente circondato da un gas rarefatto e freddo
(ossia piú freddo del solido), produce luce con uno spettro quasi
continuo contenente linee scure dipendenti dal tipo di atomi che
costituiscono il gas.
1.1.2. Il reticolo di diffrazione
Per la determinazione delle lunghezze d’onda associate alle linee spettrali, un metodo di gran lunga piú preciso rispetto al prisma è quello
del reticolo di diffrazione13 , generalizzazione del dispositivo sperimen13. http://it.wikipedia.org/wiki/Reticolo_di_diffrazione.
I.
Fisica atomica
15
tale per l’interferenza della luce trasmessa attraverso due fenditure
con il quale Young nel 1801 forní evidenza sperimentale della natura
ondulatoria della luce.
Un reticolo di diffrazione è costituito da una lastra opaca alla luce (opaca nell’intervallo di lunghezze d’onda rilevanti per la misura) con N
fenditure equispaziate. La luce, emessa da una sorgente monocromatica
talmente lontana (nel disegno, a sinistra) da poter essere considerata
puntiforme e produrre un’onda piana in prossimità della lastra, passa
attraverso le fenditure e viene raccolta su uno schermo fotosensibile che
si trova lontano, dalla parte opposta alla sorgente (nel disegno, sulla destra; qui “lontano” vuol dire che la distanza fra schermo e lastra è molto
maggiore della distanza fra fenditure). Data la simmetria dell’apparato,
il dispositivo può essere studiato in due dimensioni. Se nella lastra ci
fosse un solo forellino puntiforme, o una singola fenditura rettilinea infinitamente sottile, al di là della lastra l’onda piana luminosa incidente
diventerebbe un’onda sferica, o, rispettivamente, cilindrica (principio
di Huygens). Se, anziché una sola, abbiamo N fenditure rettilinee equispaziate, le N onde cilindriche uscenti dalle N fenditure equispaziate
(il termine reticolo allude alla regolarità spaziale delle fenditure sulla
lastra opaca) interferiscono fra loro; la loro interferenza produce sullo
Figura 1.2. Dispositivo di Bunsen e Kirchhoff.
16
Elementi di fisica atomica, molecolare e dei solidi
Figura 1.3. Cammini ottici della luce diffratta da una doppia fenditura.
schermo l’alternanza di zone, o frange, o righe piú o meno luminose,
dalla quale è possibile risalire alla lunghezza d’onda della luce incidente14 . Il piú semplice “reticolo di diffrazione” è naturalmente quello
dell’esperimento di Young, costituito da una lastra opaca sulla quale
sono praticate N = 2 fenditure come in Fig. 1.3. L’effetto dell’interferenza
sull’intensità ci interessa in prossimità dello schermo, lontano dalle fenditure. Qui le le due onde cilindriche possono essere considerate onde
piane ψ1 = eik(x+∆x) e ψ2 = eikx dove x e x + ∆x sono i rispettivi cammini
ottici e k = 2π/λ il numero d’onda della radiazione monocromatica; l’intensità luminosa risulta quindi proporzionale a |ψ1 + ψ2 |2 = 2 + 2 cos(k∆x)
i cui massimi sono in corrispondenza di k∆x = 2nπ con n intero, dove
il coseno vale +1. Poiché (vedi Fig. 1.3) ∆x = d sin ϑ otteniamo per i
massimi di intensità:
cos(k∆x) = +1 ⇐⇒ k∆x = 2nπ ⇐⇒
d sin ϑ
λ
= n;
(1.1)
(n intero qualunque).
Cosí, dalla posizione angolare dei massimi di intensità della luce sullo schermo e dalla conoscenza del parametro sperimentale d (distanza
fra le fenditure), si ricava la lunghezza d’onda della luce monocro14. In esperimenti di questo tipo il diametro del forellino o la larghezza della fenditura non
sono quasi mai trascurabili rispetto alla lunghezza d’onda della luce. Per questo motivo l’intensità
luminosa registrata sullo schermo, oltre che dall’interferenza fra i fasci uscenti dalle diverse
fenditure, è anche modulata dagli effetti di diffrazione dovuti alla singola fenditura, in grado di
I.
Fisica atomica
17
matica che la sorgente ha inviato sulle due fenditure. Il parametro n
viene chiamato ordine, e caratterizza il particolare massimo di intensità
diffratta in corrispondenza di un certo angolo ϑ ; data la simmetria del
sistema, se per l’angolo ϑ c’è un massimo di ordine n, ce n’è anche uno
di ordine −n in corrispondenza dell’angolo −ϑ . L’ordine di diffrazione
n= 0 corrispondente alla direzione di trasmissione diretta è unico.
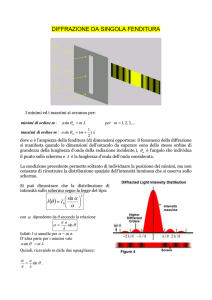
L’utilizzo della doppia fenditura per l’analisi delle linee spettrali
presenta problemi di risoluzione: le linee corrispondenti ai massimi
di intensità, dove avviene l’interferenza costruttiva, risultano abbastanza sfocate (vedi Fig. 1.4, in basso). Per aumentare la risoluzione
dell’immagine diffratta si può aumentare il numero di fenditure. Con
2N + 1 fenditure l’intensità della radiazione sullo schermo è infatti
proporzionale a:
2
N h
N
i 2 X
ikx X ik(x+m∆x)
ik(x−m∆x) e
+e
cos(mk∆x) ;
e +
= 1 + 2
m=1
(1.2)
m=1
dove la posizione dei massimi è ancora data dall’Eq. (1.1), ovvero
quando in Eq. (1.2) tutti e N i coseni valgono +1: maggiore è il numero
di fenditure, piú alto è il picco. Fuori dai massimi si ha invece una
somma di valori negativi e positivi con media piccola o nulla, che non
cresce al crescere di N (vedi Fig. 1.4, in alto)15 .
1.1.3. Lo spettro dell’idrogeno
Un’ampolla riempita di idrogeno e posta tra gli elettrodi di un trasformatore da 5000 Volts (lampada a scarica) emette luce visibile e
ultravioletta. Usando uno spettrometro a diffrazione con uno schermo
sensibile alla radiazione ultravioletta/visibile/infrarossa, è possibile
misurare le lunghezze d’onda λ caratteristiche della radiazione elettromagnetica prodotta dalla scarica nel gas. Si osserva una grande
regolarità, la cui matematizzazione e interpretazione ha storicamente
dato inizio alla comprensione dei fenomeni microscopici per mezzo
della teoria quantistica: l’inverso 1/λ si esprime accuratamente (vedi
Tabella 1.1) in termini di semplicissime serie numeriche moltiplicate
per un’unica costante dimensionale R (pari a ≈ 109677 se misuriamo le
lunghezze d’onda inverse in cm−1 come fanno gli spettroscopisti).
modificare l’altezza dei massimi ma non la loro posizione in funzione della lunghezza d’onda.
15. Si può mostrare che per N → ∞ l’Eq. (1.2) tende a una somma di funzioni delta di Dirac.