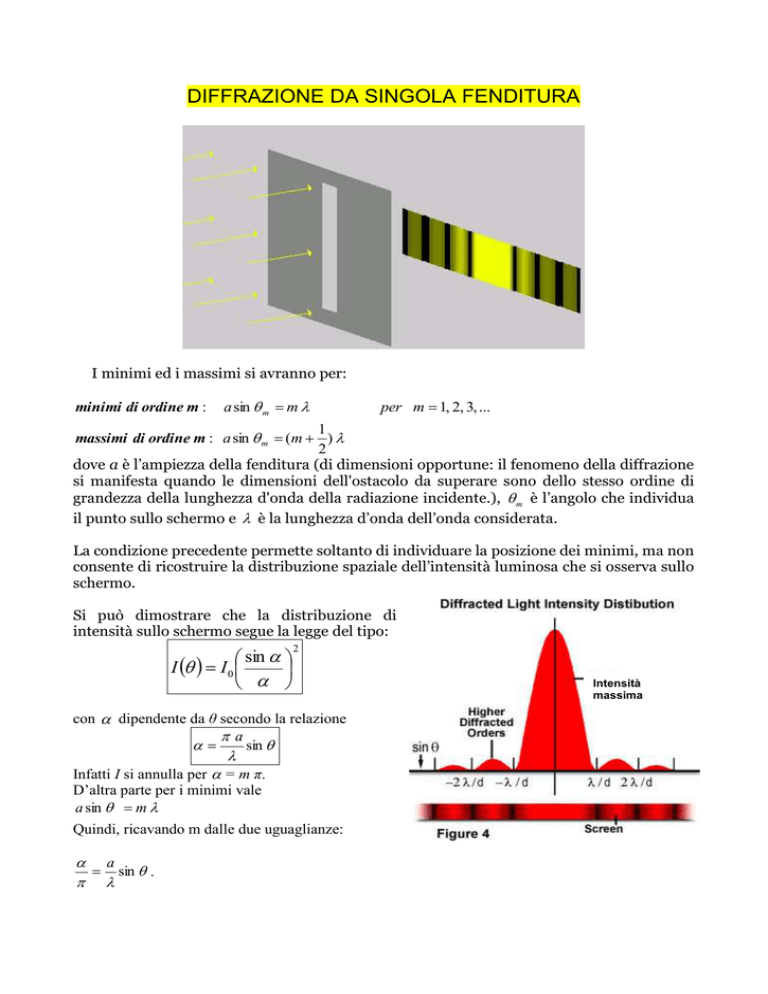
DIFFRAZIONE DA SINGOLA FENDITURA
I minimi ed i massimi si avranno per:
minimi di ordine m :
a sin m m
per m 1, 2, 3, ...
1
massimi di ordine m : a sin m (m )
2
dove a è l’ampiezza della fenditura (di dimensioni opportune: il fenomeno della diffrazione
si manifesta quando le dimensioni dell'ostacolo da superare sono dello stesso ordine di
grandezza della lunghezza d'onda della radiazione incidente.), m è l’angolo che individua
il punto sullo schermo e è la lunghezza d’onda dell’onda considerata.
La condizione precedente permette soltanto di individuare la posizione dei minimi, ma non
consente di ricostruire la distribuzione spaziale dell’intensità luminosa che si osserva sullo
schermo.
Si può dimostrare che la distribuzione di
intensità sullo schermo segue la legge del tipo:
sin
I I 0
2
con dipendente da θ secondo la relazione
a
sin
Infatti I si annulla per = m π.
D’altra parte per i minimi vale
a sin m
Quindi, ricavando m dalle due uguaglianze:
a
sin .
Intensità
massima
Il primo massimo dopo la frangia
centrale si ha per m=1, perciò per
= 3 π /2, sin = -1 e quindi
I1 = I0 (-2 /(3 π))2 = 0,04 I0.
Il secondo massimo si ottiene per
= 5 π /2 e quindi
I2= I0 (-2 /(5 π))2 = 0,016 I2.
e così via.
I successivi massimi dello spettro di
diffrazione hanno quindi intensità
fortemente decrescenti.
Possiamo ora riflettere sulle condizioni per le quali è visibile la diffrazione. Dovendo sinθ essere
sempre minore o uguale ad 1, considerando il massimo di ordine m, risulta di conseguenza
1
(m )
2 1 , da cui.
sin m
a
1
3
5
7
9
a (m )
,
,
,
.
2
2
2
2
2
Ne segue che, per poter osservare distintamente i primi 4 ordini di diffrazione, gli unici visibili
chiaramente per questioni di intensità, deve essere almeno:
9
a . Sperimentalmente si pone quasi sempre a 5 .
2
DIFFRAZIONE DA DUE FENDITURE
Consideriamo un sistema di due fenditure come nell’esperimento di Young. Sia a la loro
larghezza e b la distanza tra i loro centri.
La situazione reale prodotta sullo schermo non può prescindere dal fatto che le sorgenti
non possono essere puntiformi come richiederebbe la situazione ideale per poter
osservare unicamente figure di interferenza. Infatti, sullo schermo posto dietro le fenditure,
si raccoglieranno diversi tipi di frange di diversa origine: infatti si sovrapporranno sia le
frange di diffrazione di ciascuna delle due fenditure, sia le frange di interferenza dovuti
all’interferenza dei due fasci diffratti.
Nel caso in cui luce di lunghezza d’onda passi attraverso fenditure di larghezza a<<, le
frange di interferenza hanno tutte la stessa ampiezza.
Se, invece, la fenditura ha ampiezza a, le frange di interferenza sono modulate dalla
figura di diffrazione e l’ampiezza risultante sullo schermo è composta da frange
d’interferenza di ampiezza variabile modulata dalla figura di diffrazione.
RETICOLI DI DIFFRAZIONE
L’interferenza a due fenditure con luce monocromatica
L’immagine sopra mostra l’andamento dell’intensità in una figura d’interferenza ottenuta
facendo passare luce monocromatica attraverso due fenditure di larghezza a la cui
distanza d supera di 4 volte la larghezza a. La linea tratteggiata mostrerebbe la figura di
interferenza fra sorgenti puntiformi di distanza d; quella continua sottile è la figura di
diffrazione ottenuta con una sola fenditura di larghezza a, quella continua più spessa la
situazione in esame.
Le immagini seguenti mostrano in sequenza la figura d’interferenza ottenuta con due
fenditure quando:
a
1
d
4
a
1
d
6
a
1
d
9
La diminuzione della larghezza a della fenditura produce inevitabilmente la diminuzione
dell’intensità della figura d’interferenza al punto tale che a partire da un certo valore non si
vedrebbe più niente.
http://www.ba.infn.it/%7ezito/museo/esp146/Ndif.html
L’interferenza di luce monocromatica con reticolo di diffrazione
Per ovviare a questo si può aggiungere alla fenditura di destra (o sinistra) una terza alla
stessa distanza d delle prime due e poi una quarta e così di seguito.
Senza entrare troppo in dettagli si intuisce che negli stessi punti in cui due fenditure
producevano interferenza costruttiva la si ottiene ancora (la differenza di percorso è
sempre un multiplo della lunghezza d’onda); nelle zone intermedie si ottengono massimi
secondari che aumentano di numero man mano che si aggiungono fenditure ma
diminuiscono di intensità; quelli principali invece aumentano di intensità ma diventano
sempre più puntiformi.
Nelle seguente serie di immagini si passa dall’interferenza con 2 fenditure a quella con via
via più fenditure tutte alla stessa distanza d e con la medesima larghezza a.
2 fenditure
3 fenditure
5 fenditure
8 fenditure
Se si continua ad aggiungere fenditure si realizza quello che viene chiamato un reticolo di
diffrazione: un insieme di N fenditure uguali, parallele ed equidistanti d
Le prima immagine mostra la figura di diffrazione
ottenuta con un reticolo di diffrazione con
,
(la lunghezza d’onda del laser
usato a scuola);
la seconda con
,
.
Dunque l’andamento dell’intensità prodotta da
un reticolo di diffrazione con numerose
fenditure consiste di stretti picchi
contrassegnati dal numero d’ordine m.
Le corrispondenti frange chiare viste su uno
schermo si chiamano righe e sono pure
numerate secondo il valore di m.
La posizione dei massimi è data dall’equazione:
d sin m
dove d è la distanza tra due fenditure adiacenti,
detta passo del reticolo.
Un’applicazione dei reticoli di diffrazione
Aumentando il numero delle fenditure la larghezza delle righe diminuisce. Questo
permette di evitare la sovrapposizione con le righe di lunghezza d’onda diversa.
www.ba.infn.it/~garuccio/didattica/spettroscopia/RETICOLODIDIFFRAZIONE.htm
I reticoli di diffrazione sono utilizzati per determinare la lunghezza d’onda della luce
emessa da una qualsiasi sorgente, sia essa una lampada o una stella.
Ogni sostanza emette onde elettromagnetiche con uno spettro caratteristico. Per le
sostanze gassose, normalmente lo spettro di emissione è composto da righe spettrali.
Quello riportato in figura è quello relativo all’idrogeno.
Nel produrre lo spettro di una luce policromatica un reticolo presenta, rispetto ad un
prisma, diversità e vantaggi:
Essendo meno spesso assorbe molto meno la luce di cui si vuole ottenere lo
spettro.
Mentre il prisma dà un solo spettro, il reticolo ne dà diversi.
L’angolo di deviazione nel reticolo è proporzionale alla lunghezza d’onda
(dsinθ=m), perciò viene deviato più il rosso del violetto, mentre un prisma devia più
il violetto del rosso.
Nel caso del prisma, dato che l’indice di rifrazione del vetro varia molto nel violetto,
lo spettro è largo nel violetto e molto stretto negli altri colori.
Uno
spettroscopio a
reticolo
permette di osservare l’intensità delle
righe spettrali che escono dal reticolo
G colpito dalla luce della sorgente S
focalizzata attraverso le lenti L1 e L2 e
la
fenditura
S1
orientando
semplicemente il telescopio T (cioè
variando l’angolo θ).
La riga spettrale osservata quando l’angolo vale θ =0 contiene tutte le . Invece, a causa
della dispersione, i massimi di ordine m successivo delle varie righe spettrali si osservano
a posizioni angolari θm distinte.
Perciò con uno spettroscopio a reticolo, noto il passo del reticolo, dalla misura dell’angolo
a cui si vede una riga colorata si può risalire direttamente alla lunghezza d’onda (tramite la
relazione dsinθ=m), ciò che con il prisma non si può fare.
Righe di emissione del cadmio nello spettro visibile, viste attraverso uno spettroscopio a reticolo:












