Soluzioni Primo Esonero del Corso di Ottica con Laboratorio A.A.

Soluzioni Primo Esonero del Corso di Ottica con Laboratorio
A.A. 2015-2016
11 Novembre 2015
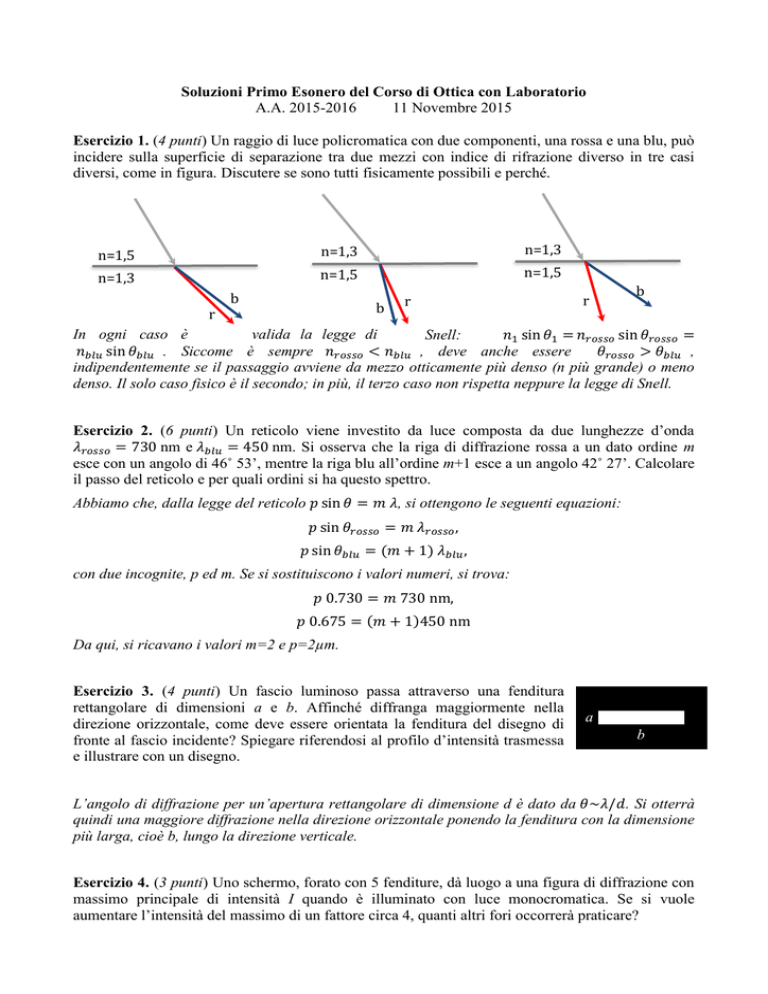
Esercizio 1. (4 punti) Un raggio di luce policromatica con due componenti, una rossa e una blu, può
incidere sulla superficie di separazione tra due mezzi con indice di rifrazione diverso in tre casi
diversi, come in figura. Discutere se sono tutti fisicamente possibili e perché.
n=1,5
n=1,3
n=1,3
n=1,3
n=1,5
n=1,5
r
b
b
r
r
b
In ogni caso è
valida la legge di
Snell:
𝑛1 sin 𝜃1 = 𝑛𝑟𝑜𝑠𝑠𝑜 sin 𝜃𝑟𝑜𝑠𝑠𝑜 =
𝑛𝑏𝑙𝑢 sin 𝜃𝑏𝑙𝑢 . Siccome è sempre 𝑛𝑟𝑜𝑠𝑠𝑜 < 𝑛𝑏𝑙𝑢 , deve anche essere
𝜃𝑟𝑜𝑠𝑠𝑜 > 𝜃𝑏𝑙𝑢 ,
indipendentemente se il passaggio avviene da mezzo otticamente più denso (n più grande) o meno
denso. Il solo caso fisico è il secondo; in più, il terzo caso non rispetta neppure la legge di Snell.
Esercizio 2. (6 punti) Un reticolo viene investito da luce composta da due lunghezze d’onda
𝜆𝑟𝑜𝑠𝑠𝑜 = 730 nm e 𝜆𝑏𝑙𝑢 = 450 nm. Si osserva che la riga di diffrazione rossa a un dato ordine m
esce con un angolo di 46˚ 53’, mentre la riga blu all’ordine m+1 esce a un angolo 42˚ 27’. Calcolare
il passo del reticolo e per quali ordini si ha questo spettro.
Abbiamo che, dalla legge del reticolo 𝑝 sin 𝜃 = 𝑚 𝜆, si ottengono le seguenti equazioni:
𝑝 sin 𝜃𝑟𝑜𝑠𝑠𝑜 = 𝑚 𝜆𝑟𝑜𝑠𝑠𝑜 ,
𝑝 sin 𝜃𝑏𝑙𝑢 = (𝑚 + 1) 𝜆𝑏𝑙𝑢 ,
con due incognite, p ed m. Se si sostituiscono i valori numeri, si trova:
𝑝 0.730 = 𝑚 730 nm,
𝑝 0.675 = (𝑚 + 1)450 nm
Da qui, si ricavano i valori m=2 e p=2µm.
Esercizio 3. (4 punti) Un fascio luminoso passa attraverso una fenditura
rettangolare di dimensioni a e b. Affinché diffranga maggiormente nella
direzione orizzontale, come deve essere orientata la fenditura del disegno di
fronte al fascio incidente? Spiegare riferendosi al profilo d’intensità trasmessa
e illustrare con un disegno.
a
b
L’angolo di diffrazione per un’apertura rettangolare di dimensione d è dato da 𝜃~𝜆/𝑑. Si otterrà
quindi una maggiore diffrazione nella direzione orizzontale ponendo la fenditura con la dimensione
più larga, cioè b, lungo la direzione verticale.
Esercizio 4. (3 punti) Uno schermo, forato con 5 fenditure, dà luogo a una figura di diffrazione con
massimo principale di intensità I quando è illuminato con luce monocromatica. Se si vuole
aumentare l’intensità del massimo di un fattore circa 4, quanti altri fori occorrerà praticare?
L’intensità di un massimo di diffrazione da un reticolo è proporzionale al quadrato del numero
totale di fenditure N. Se si vuol far aumentare l’intensità di un fattore 4, occorrerà quindi
aumentare N di un fattore 2. Notiamo che la relazione è approssimata, perché la formula completa
è 𝐼 = 𝐼0 sin2(𝑁𝜙)/sin2 (𝜙).
Esercizio 5. (5 punti) Un recipiente pieno d’acqua (densità 1 kg/dm3) è sospeso a un’altezza di 10m
dal suolo. Quale deve essere il modulo di un campo magnetico uniforme che, riempiendo lo stesso
volume del recipiente, ha un’energia associata di valore pari a quella gravitazionale dell’acqua?
Si debbono uguagliare le energie del campo magnetico e quella gravitazionale. L’equazione da
scrivere è:
𝐵2
𝑚𝑔ℎ =
𝑉
2 𝜇0
𝐵2
dove V è il volume del recipiente e va inserito perché l’espressione 2 𝜇 è una densità di energia.
0
Dividendo membro a membro per il volume, si trova:
𝐵2
𝜌𝑔ℎ =
2 𝜇0
kg
kg
3 kg
con 𝜌 = 1 dm3 = 1 (10−1 m)3 = 10 m . Da questa possiamo trovare il valore del campo magnetico
come
𝐵 = √2 𝜇0 𝜌𝑔ℎ = 0.5 T.
Esercizio 6. (10 punti) Se si osservano le righe di emissione di una lampada spettrale all’idrogeno,
si trova che il loro spettro è descritto bene da una legge del tipo:
1
𝜆
1
1
= 𝐶(4 − 𝑘 2 )
dove 𝜆 è la lunghezza dell’emissione e k è un numero intero. Una misura k
𝜆 (nm)
sperimentale produce i dati riportati nella tabella, in cui le lunghezze d’onda
657.05
hanno un errore percentuale dello 0.1%. Tale errore è dovuto alla risoluzione 3
4
486.28
del reticolo impiegato per le misure.
(a) Sapendo che il reticolo impiegato per le misura ha larghezza L=1cm e 5
434.07
che le righe sono misurate al primo ordine, quale è il suo passo?
6
410.60
(b) Controllare se la colonna delle lunghezze d’onda è formattata
7
396.86
correttamente e, nel caso, riscriverla.
388.82
(c) Trovare la linearizzazione conveniente per poter ricavare il valore della 8
384.42
costante dimensionale C da una regressione lineare e indicare tale 9
valore con il suo errore.
(d) Produrre un grafico di 𝜆 in funzione di k e un grafico con le grandezze usate per la sua
linearizzazione.
(a) L’incertezza 𝛥𝜆 sulla lunghezza d’onda 𝜆 è dettata solo dalla risoluzione, quindi si deve
𝛥𝜆
imporre 𝜆 = 1/𝑅, con R il potere risolutivo del reticolo. Questo è dato da 𝑅 = 𝑚 𝑁, con
m il numero d’ordine cui si risolve lo spettro (nel nostro caso m=1) ed N il numero totale
𝛥𝜆
di fenditure del reticolo. Abbiamo allora che 𝜆 = 0.001, quindi R=1000. La lunghezza del
reticolo è L=1 cm =10 mm, da cui si trova la densità di righe n = N/L = R/L =100
righe/mm. Il passo è quindi p=1/n = 1/100 mm = 10 µm.
(b) A ciascuna lunghezza d’onda possiamo associare un errore pari a 0.001 𝜆; esplicitando i
calcoli, si trova che i valori delle lunghezze d’onda sono significativi solo fino alla prima
cifra decimale. Bisogna quindi riscrivere la tabella come segue:
𝜆 (nm)
657.1
486.3
434.1
410.6
396.9
388.8
384.4
k
3
4
5
6
7
8
9
1
1
1
seguire
diverse
1
1
𝑥 = 4 − 𝑘 2 , 𝑦 = 𝜆,
4𝑘 2
(c) Si possono
linearizzazione:
da cui l’equazione di primo grado 𝑦 = −𝐶 𝑥 + 4 𝐶;
𝑥 = 𝑘 2 , 𝑦 = 𝜆,
1
𝛥𝜆 (nm)
0.7
0.5
0.4
0.4
0.4
0.4
0.4
𝑥 = 𝑘 2 −4 , 𝑦 = 𝜆,
da cui l’equazione di primo grado 𝑦 = 𝐶 𝑥;
𝑥
da cui l’equazione di primo grado 𝑦 = 𝐶
Dalla regressione si ottiene il valore
𝐶 = (0.010964 ± 0.000004) nm−1 = (10.964 ± 0.004)μm−1
scelte
per
la
(d) Il grafico “sperimentale” richiesto in tutti i casi è quello delle grandezze misurate:
700
650
600
550
500
l (nm)
450
400
350
300
2
4
6
k
8
Sulla base della scelta della scala, le incertezze possono non essere visibili: bisogna commentarlo.
10
1
1
Il secondo grafico da produrre dipende dalla linearizzazione scelta: se si opta per 𝑥 = 4 − 𝑘 2 ,
1
𝑦 = 𝜆, i punti si debbono allineare lungo una retta passante per l’origine.
y (nm^1)
0.0034000
0.0032000
0.0030000
y = 0.011x
R² = 0.99996
0.0028000
0.0026000
0.0024000
0.0022000
0.0020000
0.0018000
0.0016000
0.0014000
0.10000
0.15000
0.20000
x
0.25000
0.30000