Prova di recupero corso di Fisica 4
8/05/2007 I parte
Esercizi numerici
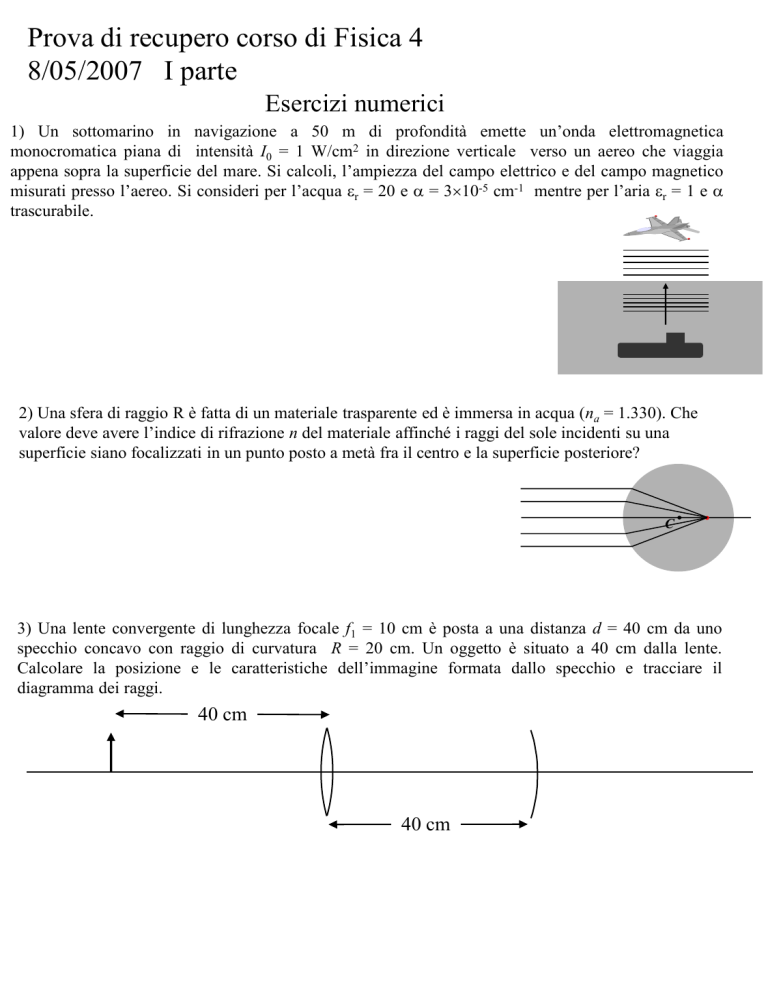
1) Un sottomarino in navigazione a 50 m di profondità emette un’onda elettromagnetica
monocromatica piana di intensità I0 = 1 W/cm2 in direzione verticale verso un aereo che viaggia
appena sopra la superficie del mare. Si calcoli, l’ampiezza del campo elettrico e del campo magnetico
misurati presso l’aereo. Si consideri per l’acqua r = 20 e = 310-5 cm-1 mentre per l’aria r = 1 e
trascurabile.
2) Una sfera di raggio R è fatta di un materiale trasparente ed è immersa in acqua (na = 1.330). Che
valore deve avere l’indice di rifrazione n del materiale affinché i raggi del sole incidenti su una
superficie siano focalizzati in un punto posto a metà fra il centro e la superficie posteriore?
C
3) Una lente convergente di lunghezza focale f1 = 10 cm è posta a una distanza d = 40 cm da uno
specchio concavo con raggio di curvatura R = 20 cm. Un oggetto è situato a 40 cm dalla lente.
Calcolare la posizione e le caratteristiche dell’immagine formata dallo specchio e tracciare il
diagramma dei raggi.
40 cm
40 cm
Quesiti (MAX 30 parole)
A) Cosa è e da quale parametro viene definita la riflessione totale interna?
B) Spiegare come si può ottenere luce polarizzata linearmente partendo da luce non polarizzata e
usando una lastra di vetro
C) Perché dei pezzi di vetro incolore sono meno visibili immersi in acqua di quanto lo siano in aria?
D) Scrivere la forma Newtoniana dell’equazione delle lenti specificando il significato dei termini
E) Spiegare il fenomeno dell’aberrazione sferica e le sue cause
Soluzioni
dalla teoria del diottro concavo acqua/polimero sarà:
1)
f'
n2 R
nR
nR
3
R
n2 n1
n na
n 1.33
2
da cui: n = 3.99
EA
2)
dove: n
2Te -x I 0 Z0 2
2 I A Z0
r
e
na 1
4na n
na n
EA 1969.6 V
quindi:
BA
3)
-x
e
I 0 Z0
2
m
E
6.56 10-6 T
c
40 cm
F
C
40 cm
lente:
1
1
1
s1
s1 '
f
s1 '
f s1
13.3 cm
s1 f
m1
specchio:
s2 '
1
1
2
s2
s2 '
R
R
s2
16 cm
R
2 s
2
2
s1 '
0.33
s1
con s2 d s1 ' 26.67 cm
m
s1 ' s2 '
0.2
s1 s2
Prova di recupero corso di Fisica 4
8/05/2007 II parte
Esercizi numerici
1) A quale distanza reciproca minima dm devono essere poste due sorgenti di onde radio sferiche
monocromatiche in aria ( = 900 MHz) affinché si abbia un minimo di campo elettrico nel punto O a
distanza D = 5 m da una delle due sorgenti?
d
D
O
2) Un’estesa sorgente di luce ( = 632 nm) illumina a incidenza normale due lastre di vetro (nV = 1.70)
lunghe 10 cm che si toccano ad un'estremità e sono separate da un sottile filo di di spessore D posto
all’altra estremità. Lo spazio fra le due lastre è riempito di olio con n = 1.40. Compaiono in totale
esattamente 8 frange scure. Calcolare il valore dello spessore D.
luce incidente
10 cm
3) Due fenditure ciascuna di apertura D e a distanza reciproca t = 20 mm sono illuminate da luce sotto
forma di onda piana coerente di lunghezza d’onda =530 nm. Si osserva che i primi minimi di intensità
da diffrazione delle due fenditure si sovrappongano su uno schermo distante d = 3 m. Quanto vale
l’apertura D?
t
d
Quesiti (MAX 30 parole)
A) Definire la coerenza spaziale e temporale.
B) Disegnare in modo qualitativo la relazione di dispersione tipica di un vetro nel visibile.
C) Disegnare in modo qualitativo lo spettro di assorbimento tipico di un gas molecolare.
D) Cosa è la fluorescenza?
E) Dati tre punti sul diagramma CIE 1932, quali colori si possono ottenere per mescolanza additiva?
Soluzioni
1)
dalla condizione di minimo di interferenza del primo ordine:
d 2 D2 D
2
da cui:
d
2)
1 D
4
2
dalla teoria dell’interferenza nelle lamine sottili e considerando che la
prima frangia scura appare all’estremità di contatto:
D ( N 1)
3)
2
c 1 vD
1.295 m
v 4 c
2n
1.58 10-6 m
dalla figura, per costruzione, e dalla legge di diffrazione di Fraunhofer:
ymin d
D
t
2
D
2d
159 m
t












