Secondo Esonero del Corso di Ottica con Laboratorio
A.A. 2015-2016
13 gennaio 2016
Esercizio 1. (6 punti) In laboratorio due studenti hanno realizzato indipendentemente misure del
potere rotatorio specifico su due set di soluzioni zuccherine incognite, usando celle di medesima
lunghezza (29.9±0.2)cm, riempite con soluzioni a differenti concentrazioni. I risultati delle misure
sperimentali sono riportati nella tabella seguente.
Set studente 1
c (g/cm3)
(˚)
0.02
10
0.05
21
0.10
38
Set studente 2
c (g/cm3)
(˚)
0.05
22
0.10
38
0.20
70
Gli errori sugli angoli sono di 5˚.
(1) Si deduca il tipo di attività ottica (destrogira o levogira) sulla base dei due valori del potere
rotatorio specifico ottenuti per regressione lineare utilizzando la tabella.
(2) Discutendo la compatibilità dei risultati finali dei due studenti, concludere se queste misure si
riferiscono o no allo stesso materiale otticamente attivo.
Facendo una regressione di alpha in funzione della concentrazione c troviamo come valori dei
coefficienti angolari (nelle unità di misura appropriate u.d.m.) (390±20)u.d.m. e (360±20)u.d.m.
rispettivamente. Quando andiamo a ricavare da qui i valori dei coefficienti k troviamo: (13.1±0.8)
u.d.m. e (12.0±0.7) u.d.m. risultati di misure diverse ma che possiamo riferire allo stesso materiale
destrogiro poiché compatibili entro gli errori.
Esercizio 2. (6 punti) La lastra di vetro della vetrina di un negozio ha ricevuto un trattamento ottico
particolare sulla sua faccia interna. Infatti, quando la vetrina è illuminata dall’interno con luce
policromatica, un osservatore dall’esterno vede il vetro di colore rosso (=720nm), mentre un
cliente dall’interno vede lo stesso vetro di colore blu (=450nm). Il materiale depositato su vetro ha
indice di rifrazione 1.4 e il vetro ha indice di rifrazione 1.5.
1) Tenendo presente il fenomeno dell’interferenza della luce in riflessione e in trasmissione,
calcolare lo spessore della lastra di vetro richiesto per ottenere questo effetto. Si consiglia di
far uso di un disegno per indicare la direzione dei raggi di luce esplicativi del fenomeno.
Ricordiamo che la luce policromatica attraversando una lastra di vetro non dà luogo alla
dispersione cromatica come invece avviene nel caso del prisma ottico.
Lo spessore del trattamento deve dare interferenza costruttiva in riflessione per =450nm e
distruttiva per =720nm. Siccome i due sfasamenti alle interfacce si compensano, le condizioni
sono:
2𝑛𝑑 = 𝑚𝑏 𝜆𝑏
2𝑛𝑑 = (𝑚𝑟 +1/2)𝜆𝑟
Da qui si trova che
2𝑚𝑏
2𝑚𝑟
8
= 5 , per cui 𝑚𝑏 = 4, 𝑚𝑟 = 2. Quindi lo spessore sarà 𝑑 =
+1
0.59μm.
1
4 𝜆𝑏
2𝑛
=
Esercizio 3. (4 punti) Un reticolo diffrange luce su di una lastra di vetro con indice di rifrazione
n=1.52.
1) Si trovi il passo necessario affinché luce con =0.532µm arrivi sulla lastra ad angolo di
Brewster per m=3.
L’angolo di Brewster per questo materiale è 56.6º. La formula del reticolo poi ci dice che
𝑝 sin 𝜃𝐵 = 3𝜆, da cui si ricava 𝑝 = 1.91μm.
Esercizio 4. (4 punti) L’espressione del campo elettrico di un fascio luminoso è:
𝐸⃗ = 𝐸𝐻 cos(𝜔𝑡) 𝑖⃑ + 𝐸𝑉 sin(𝜔𝑡) 𝑗⃑
con 𝐸𝐻 ≠ 𝐸𝑉 .
1) A quale stato di polarizzazione questo corrisponde (lineare, circolare, ellittica)?
2) Sapendo che l’intensità della componente orizzontale vale 𝐼𝐻 e che, al tempo 𝑡 = 𝜋/(4𝜔) ,
l’intensità totale vale 𝐼𝑡 , si trovi qual è il valore dell’intensità della componente verticale 𝐼𝑉 , e in
quale istante di tempo l’intensità totale è pari alla sola componente 𝐼𝑉 .
Al tempo 𝑡 = 𝜋/(4𝜔) abbiamo che 𝐼𝑡 =
quando 𝑡 = 𝜋/(2𝜔).
𝐼𝐻 +𝐼𝑉
2
, quindi 𝐼𝑉 = 2𝐼𝑡 − 𝐼𝐻 . L’intensità 𝐼𝑉 viene raggiunta
Esercizio 5. (3 punti) Un fascio di luce polarizzata orizzontalmente attraversa tre polarizzatori e in
ogni passaggio perde il 20% della propria intensità.
1) Qual è la posizione angolare dell’asse di ciascun polarizzatore rispetto alla verticale?
Per avere una trasmissione dell’80%, occorre che l’angolo tra polarizzazione e asse valga 26.57º.
Le posizioni cercate sono quindi: 63.43º, 36.87º e 10.30º, riferite alla verticale come chiede il
problema.
Esercizio 6. (2 punti) Per un reticolo di diffrazione qual è il vantaggio nell’avere (a) molte fenditure
e (b) fenditure molto vicine?
Ricordando la formula p= 1/( n/mm) tra passo p di un reticolo di diffrazione ed il n° di fenditure
per mm( n/mm), possiamo affermare che la relazione è di proporzionalità inversa .
a) La figura di diffrazione da reticolo con passo piccolo e quindi con molte fenditure, a parità
di dimensione del reticolo, presenta massimi secondari più distanziati per la formula
senm =m n .Inoltre se abbiamo molte fenditure il potere Risolutivo del reticolo aumenta.
b) Se le fenditure sono molto vicine gli ordini superiori( m>1) vengono a mancare.
Esercizio 7. (2 punti) Un fascio di luce bianca incide su (a) un reticolo di diffrazione e (b) un
prisma. In entrambi i casi compare un arcobaleno su un muro, giusto al di sotto della direzione
incidente del fascio incidente orizzontale. Qual è nei due casi il colore all’estremità superiore
dell’arcobaleno?
Nello spettro di dispersione dovuto al prisma la radiazione rossa è la meno deviata e la violetta è
la più deviata, mentre per il reticolo la sequenza si inverte.
Esercizio 8. (2 punti) Di quanto devono differire i cammini di due fasci di luce provenienti dalla
stessa sorgente per interferire distruttivamente.
2
Se la distanza percorsa differisce di (m/2)conmcioè un n° dispari di i due fasci si
trovano in opposizione di fase e differiscono distruttivamente
Esercizio 9. (2 punti) Perché la luce che proviene dai due fari di un’automobile lontana non
produce una figura d’interferenza?
Perché i due fasci di luce provengono da sorgenti non coerenti e quindi non in fase.
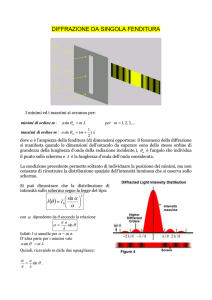
Esercizio 10. (2 punti) Nel caso della diffrazione della luce da una singola fenditura che effetto si
ha (a) aumentando la larghezza della fenditura oppure (b) la lunghezza d’onda.
a) L’intensità aumenta e la figura di diffrazione si stringe perché è inversamente
proporzionale alla larghezza della fenditura.
b) Aumentando la della radiazione la figura di diffrazione si allarga perché sen=X/L =m d
3