Relazioni fra lati ed angoli di un triangolo - Notebook Italia
annuncio pubblicitario
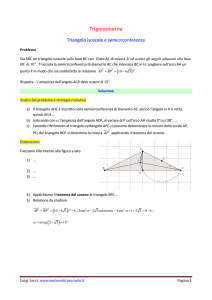
RELAZIONI FRA LATI ED ANGOLI DI UN TRIANGOLO TEOREMA. In ogni triangolo, se due lati sono disuguali, al lato maggiore è opposto l’angolo maggiore. Hp തതതത > ܥܤ തതതത ܥܣ Th ܣ > ܤመ Dimostrazione തതതത ≅ ܥܤ തതതത . Il triangolo ܤܥܦrisulta Sul lato maggiore ܥܣprendiamo un punto D in modo che ܥܦ ܤܥ ≅ ܤ ܦ. L’angolo ܦܥ ܤè un angolo esterno al triangolo ܦܤܣe quindi isoscele, quindi ܦܥ ܣܦ > ܤመܤ. Anche ܤܥ ܣܦ > ܦመܤ, ma ܤܥ ܤܥ > ܣ ܣܦ > ܦመܤ, quindi ܤ > ܣመ, come volevasi ܦܥ dimostrare. 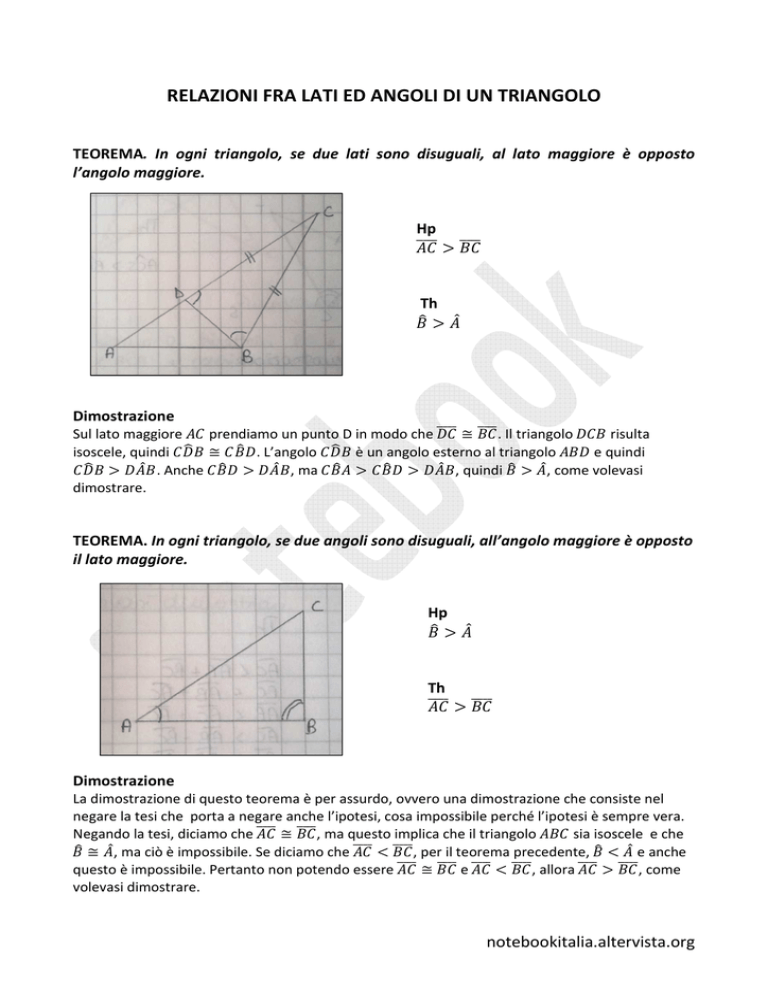TEOREMA. In ogni triangolo, se due angoli sono disuguali, all’angolo maggiore è opposto il lato maggiore. Hp ܤ > ܣመ Th തതതത > ܥܤ തതതത ܥܣ Dimostrazione La dimostrazione di questo teorema è per assurdo, ovvero una dimostrazione che consiste nel negare la tesi che porta a negare anche l’ipotesi, cosa impossibile perché l’ipotesi è sempre vera. തതതത ≅ ܥܤ തതതത , ma questo implica che il triangolo ܥܤܣsia isoscele e che Negando la tesi, diciamo che ܥܣ መ തതതത < ܥܤ തതതത , per il teorema precedente, ܤ < ܣመ e anche ܣ ≅ ܤ, ma ciò è impossibile. Se diciamo che ܥܣ തതതത ≅ ܥܤ തതതത e ܥܣ തതതത < ܥܤ തതതത , allora ܥܣ തതതത > ܥܤ തതതത , come questo è impossibile. Pertanto non potendo essere ܥܣ volevasi dimostrare. notebookitalia.altervista.org TEOREMA. In ogni triangolo ciascun lato è minore della somma degli altri due ed è maggiore della loro differenza. Th തതതത < ܤܣ തതതത + തതതത ܥܣ ܥܤ തതതത തതതത തതതത ܤܣ < ܥܤ+ ܥܣ തതതത < ܥܣ തതതത + ܥܤ തതതത ܤܣ തതതത > ܤܣ തതതത − ܥܤ തതതത ܥܣ തതതത − ܥܣ തതതത തതതത > ܤܣ ܥܤ തതതത > ܥܣ തതതത − ܥܤ തതതത ܤܣ Dimostrazione Nel triangolo ܥܤܣ, per costruzione, il lato ܤܣè maggiore degli altri. Quindi, le prime due relazioni തതതത < ܤܣ തതതത e di conseguenza ܥܣ തതതത < ܤܣ തതതത + ܥܤ തതതത e ܥܤ തതതത < ܤܣ തതതത e quindi della tesi sono ovvie, essendo ܥܣ തതതത < ܤܣ തതതത + ܥܣ തതതത . Ci limitiamo a dimostrare la terza relazione. ܥܤ തതതത ≅ ܤܥ തതതത. Il triangolo ܤܦܥè isoscele sulla base Prolunghiamo ܥܣdalla parte di C di un segmento ܦܥ ܤܣ < ܤ ܦ DB e quindi ܦ ܤܥ ≅ ܤܦܥ. Consideriamo ora il triangolo ܦܤܣ. Di esso sappiamo che ܦܣ ܤè congruente ad una parte di ܤܣ ܲ. Quindi, poiché in un triangolo, all’angolo perché ܦܣ തതതത > ܤܣ തതതത , ma ܦܣ തതതത ≅ ܥܣ തതതത + ܦܥ തതതത e poiché തതതത തതതത, avremo ܤܥ ≅ ܦܥ maggiore è opposto il lato maggiore, ܦܣ തതതത ≅ ܥܣ തതതത + ܤܥ തതതത. Da ciò ܤܣ തതതത < ܥܣ തതതത + ܤܥ തതതത , come volevasi dimostrare. ܦܣ തതതത + ܤܥ തതതത > ܤܣ തതതത . A ciascun membro sottraiamo Quest’ultima relazione la scriviamo al contrario: ܥܣ തതതത e poi ܤܥ തതതത, otteniamo così: ܥܣ തതതത + ܤܥ തതതത − ܥܣ തതതത > ܤܣ തതതത − ܥܣ തതതത E ܥܣ തതതത + ܤܥ തതതത − ܤܥ തതതത > ܤܣ തതതത − ܤܥ തതതത. prima ܥܣ Dimostriamo così le altre relazioni. തതതത > ܥܣ തതതത − ܥܤ തതതത è ovvia siccome ܤܣ തതതത > ܥܣ തതതത , quindi ܤܣ തതതത > ܥܣ തതതത − ܤܥ തതതത, come L’ultima relazione, ܤܣ volevasi dimostrare. notebookitalia.altervista.org
