CONCETTI DI CALCOLO DELLE PROBABILITA’
DEFINIZIONI
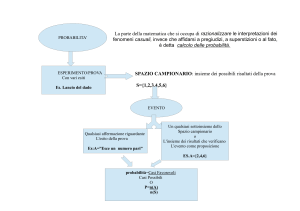
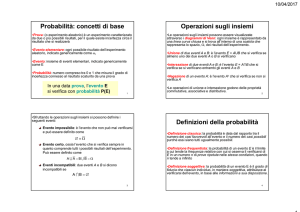
Prova casuale o aleatoria:
processo o esperimento di cui non è possibile conoscere con certezza
la risposta prima di averlo compiuto (ad es. il lancio di un dado)
Evento:
ogni possibile esito dell’esperimento aleatorio, in genere indicato con
una lettera maiuscola (A, B, E, A1, A2, ...). Gli eventi possono essere
anche rappresentati con proposizioni
Spazio campionario:
insieme degli eventi/esiti possibili di un esperimento casuale.
Viene indicato generalmente con Ω, ma anche con la lettera U (universo)
oppure S (spazio).
Qualsiasi sottoinsieme dello spazio campionario è un evento.
Evento semplice/elementare: sottoinsieme delle spazio campionario formato da un unico elemento
Evento composto:
Esempio:
Prova lancio di un dado
è il risultato dell’unione di più eventi semplici (ad. es. nel lancio di un dado,
l’evento “ esce un numero pari “ )
Ω = spazio campionario = {1, 2, 3, 4, 5, 6}
Eventi semplici = {1}, {2}, {3}, {4}, {5}, {6}
Evento composto = {esce un numero pari} = {2, 4, 6}
Evento certo:
evento che sicuramente si verifica ad ogni prova (evento VERO).
E’ rappresentato dall’ insieme universo Ω
Evento impossibile:
evento che non può verificarsi in ogni prova (evento FALSO).
E’ rappresentato dall’ insieme vuoto ∅
L’insieme vuoto ∅ e l’insieme universo Ω sono considerati sottoinsiemi ( nella teoria degli insiemi
vengono chiamati sottoinsiemi impropri) dello spazio campionario.
Evento possibile:
evento che può verificarsi
Calcolo delle probabilità:
formula delle valutazioni numeriche della possibilità di verificarsi di
eventi casuali/aleatori
Probabilità di un evento:
probabilità classica:
non esiste un solo modo di definire la probabilità. Vi sono tre definizioni:
la probabilità di un evento E è il rapporto tra il numero dei casi
favorevoli (casi in cui si verifica l’evento considerato) e il
numero dei casi possibili ( casi che si possono sempre
n° casi favorevoli
ugualmente verificare) p(E) =
n° casi possibili
probabilità frequentista (o statistica): per conoscere la probabilità di un evento si ricorre
all’esperimento. Si può applicare quando si possono eseguire
infinite prove sull’esperimento, tutte sotto le medesime
condizioni, oppure se si fa riferimento a risultati storici (ad es.
nello studio della popolazione, alle tavole di sopravvivenza, di
mortalità, ecc….). La probabilità viene definita come
k
frequenza relativa p(E) = f = , con
n
n = numero delle prove effettuate
k = numero delle prove nelle quali l’evento si è verificato
Legge empirica del caso (Legge dei Grandi Numeri): in una serie di prove, ripetute un gran numero di
volte, eseguite tutte nelle stesse condizioni, la frequenza “tende” ad assumere valori prossimi alla
probabilità dell’evento e, generalmente, l’approssimazione è tanto maggiore quanto più numerose sono
le prove eseguite.
probabilità soggettiva:
la probabilità p(E) di un evento E è la misura del grado di fiducia che
un individuo attribuisce, in base alle sue informazioni e alle sue
opinioni, al verificarsi dell’evento E.
Utilizzeremo la probabilità classica, per cui la probabilità di un evento E è p(E) =
n° casi favorevoli
,
n° casi possibili
con 0 ≤ p(E) ≤ 1. Un evento certo ha probabilità 1 di verificarsi, viceversa se l’evento è impossibile la sua
probabilità è pari a 0. Se l’evento è possibile, la sua probabilità è compresa tra 0 e 1.
GLI EVENTI E GLI INSIEMI
L'identificazione fra eventi e sottoinsiemi di Ω permette di trasportare sugli eventi le operazioni
insiemistiche di unione (∪ ), intersezione (∩ ) e passaggio al complementare (indicato con una linea
sopra alla lettera che indica l’insieme).