eventi - Benvenuti nel secondo anno del corso di infermieristica

1
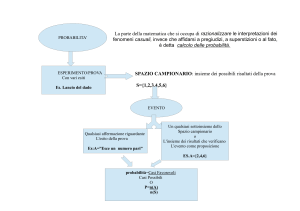
SIGNIFICATO DI PROBABILITA'
Una sperimentazione clinica dimostra che 50 pazienti trattati con farmaco A
per una determinata patologia, stanno in media, meglio di quelli trattati con
farmaco B per la stessa patologia.
1) Il trattamento A è migliore del trattamento B? (Domanda inferenziale)
2) In futuro dovrò trattare i pazienti con farmaco A piuttosto che B?
(Domanda decisionale)
Le risposte hanno un certo grado di incertezza: se margine di incertezza è
ridotto, la conclusione sarà più attendibile
Diventa importante rilevare la misura dell'incertezza, l'approccio formale è
offerto dal calcolo delle probabilità.
2
SPAZI CAMPIONARI
Definizione: Si definisce esperimento ogni processo di osservazione o misurazione.
ES.
lancio di un dado
misura dell’altezza di un campione di bambini
studio degli effetti di un farmaco sulla pressione arteriosa
Definizione: Si definisce spazio campionario S l’insieme dei posssibili risultati di un
esperimento. I singoli risultati dell’esperimento sono detti elementi o eventi semplici
di S.
ESPERIMENTO
S
Lancio di una moneta
Lancio di un dado
Misura della temperatura corporea
Lancio di due monete consecutive
Misura del sex e del fumo in un passante
T, C
1, 2, 3, 4, 5, 6
x / 34< x< 42
TT, TC, CT, CC
MF, MnF, FF, FnF
3
EVENTI
Si consideri un esperimento.
Si dice evento A ogni sottoinsieme dello spazio campionario S associato
all’esperimento stesso
AS
Esempi:
S=TT, TC, CT, CC
A: “Almeno una testa T nel lancio di due monete”
A=TT, TC, CT
S=1, 2, 3, 4, 5, 6
A: “Uscita di un numero dispari nel lancio di un dado”
A=1, 3, 5
Gli eventi e gli spazi campionari possono essere rappresentati tramite i diagrammi di
Venn:
S
A
dove l’evento è il sottoinsieme dei punti elementari ad esso inclusi.
4
EVENTO CERTO: Un evento A è certo se comprende tutti i punti dello spazio
campionario S
A=S
EVENTO IMPOSSIBILE: Un evento A si dice impossibile se non comprende alcun
punto dello spazio campionario S
A=
5
OPERAZIONI LOGICHE SUGLI EVENTI
Dato uno spazio campionario S e degli eventi Ai in esso inclusi, è possibile definire,
mediante operazioni logiche, nuovi eventi, il cui valore rimane determinato, noto
quello degli eventi dati.
UNIONE DI EVENTI: Siano A e B due eventi associati ad un esperimento: l’evento
C è definito come unione di A e B se comprende tutti i punti appartenenti ad A o B:
C=AB
S
B
A
C
Es: Nel lancio di un dado sia
A= numero pari
B= n>=4.
C=4, 5, 6
6
INTERSEZIONE DI EVENTI: Siano A e B due eventi associati ad un
esperimento: l’evento C è definito come unione di A e B se comprende tutti i punti
appartenenti sia ad A che a B:
C=AB
S
B
A
C
Es: Nel lancio di un dado sia
A= numero pari
B= n>=4.
C=4, 6
Se due eventi dello stesso spazio campionario A e B non hanno punti in comune essi
sono detti eventi disgiunti o mutuamente esclusivi perché l’occorrenza dell’uno
esclude l’altro
C=AB=.
7
COMPLEMENTAZIONE: Sia A un evento associato ad un esperimento: l’evento
complementare A è costituito dall’insieme di tutti i punti dello spazio campionario S
che non appartengono ad A.
AA=S
S
A
8
PROBABILITA’
Lo spazio campionario S rappresenta l’ambito delle possibilità di un esperimento.
Di fronte ad un evento possibile ci attribuiamo una maggiore o minore fiducia che
esso si verifichi  attribuiamo un grado di probabilità al verificarsi di un evento.
Esempi:
è probabile che oggi piova
è più probabile che il carcinoma al polmone insorga fra un fumatore che non in
un non fumatore
è più probabile che il tumore al seno insorga in una donna che ha partorito per
la prima volta dopo i 40 anni.
Il concetto di probabilità ci permette di graduare l’ambito delle possibilità e di
precisare il grado di fiducia che abbiamo nel verificarsi di un evento.
La teoria delle probabilità permette di formulare delle valutazioni numeriche di
probabilità e di assoggettarle alle regole del calcolo.
L’interpretazione di tali valori numerici dipende dal significato che attribuiamo alla
probabilità.
9
DEFINIZIONE CLASSICA DI PROBABILITA’
La probabilità di un evento E, P(E), è il rapporto tra il numero di casi favorevoli al
verificarsi dell’evento (n) e il numero di casi possibili (N):
P( E )  n / N
Esempi
Probabilità di estrarre un asso da un mazzo di 40 carte: 4/40=0.1
Probabilità di uscita croce nel lancio di una moneta: 1/2=0.5
Tale definizione vale per situazioni in cui i possibili risultati sono equiprobabili.
Scarsamente applicabile a molte situazioni reali.
10
DEFINIZIONE SOGGETTIVISTICA DI PROBABILITA’
La probabilità di un evento E è la misura del grado di fiducia, espresso tra 0 e
1, che un individuo coerente attribuisce, secondo le sue opinioni e
informazioni, sull’avverarsi di E.
11
DEFINIZIONE FREQUENTISTA DI PROBABILITA’
La probabilità di un evento E è il limite a cui tende la frequenza relativa di successo
al tendere del numero di prove all’infinito:
P ( E )  lim n / N
N 
La probabilità viene assegnata sulla base dei risultati di un esperimento ripetuto molte
volte, o sulla base di situazioni che possono essere ricondotte a tale concetto
contestuale.
Es. Probabilità che un bambino italiano nasca morto:
Pr= numero nati morti nel 1997 / numero nati nel 1997.
12
TEORIA ASSIOMATICA DELLE PROBABILITA’
Qualunque sia la definizione di probabilità, formalmente:
per probabilità intendiamo una funzione P a valori reali, definita nello spazio
campionario S che soddisfa le seguenti 3 condizioni:
1) Per ogni evento A di S:
0  P( A)  1
In particolare:
P(A)=0 se A è un evento impossibile
P(A)=1 se A è un evento certo
2)
P( S )  1
3) Se A1, A2, ……Ai,…….., sono una sequenza finita o infinita di eventi
mutuamente finiti (o disgiunti) di S allora:
P( A1  A2  ...  Ai .....)  P( A1 )  P( A2 )  ......P( Ai )  ...
13
Il modo più semplice per assegnare una funzione di probabilità allo spazio
campionario S è quello di assegnare ad ogni punto dello spazio campionario una
probabilità: la probabilità corrispondente a qualsiasi evento sarà definita
immediatamente per l’assioma 3) come somma delle probabilità corrispondenti ai
punti inclusi nell’evento.
Esempio:
Consideriamo lo spazio campionario associato al lancio consecutivo di una moneta
per 2 volte:
C
T
(C,T)
(C;C)
(T,T)
(T,C)
T
C
In base all’approccio classico di probabilità possiamo attribuire ad ogni punto dello
spazio campionario una probabilità pi=1/4.
La nostra funzione di probabilità sarà: pi=1/4per ogni iS.
La probabilità di un evento qualsiasi, ad esempio la probabilità che esca almeno una
testa, sarà:
P (CT  TC  TT )  P (CT )  P (TC )  P (TT ) 
 1/ 4  1/ 4  1/ 4  3 / 4
14
REGOLE DEL CALCOLO DELLE PROBABILITA’
1) Regole dell’addizione:
Siano A e B due eventi di S tali che AB.
P(A  B)  P(A)  P(B)  P(A  B)
S
B
A
AB
Esempio:
La probabilità di estrarre una carta rossa o una figura da un mazzo di 40 carte.
15
Se A e B sono due eventi tali che AB=:
P( A  B)  P( A)  P( B)
Esempio:
La probabilità di estrarre una figura o una carta inferiore a 2.
Se A è il complementare di A in S, allora:
P( A  A )  P ( A)  P ( A )  1
P( A )  1  P ( A)
Esempio:
Se la probabilità di morire nel I anno dalla diagnosi per un paziente affetto da Ka
polmonare è del 30%, la probabilità che un paziente sopravviva al II anno è
1_0.3=0.7.
16
2) Regola della moltiplicazione e probabilità condizionale
E’ utile conoscere la probabilità di un evento AS, quando si è verificato un altro
evento BS.
Esempi:
- Probabilità di uscita del 7 di quadri dato che è uscita una carta di quadri
- Probabilità di avere colera data gastroenterite acuta.
Tale probabilità prende il nome di probabilità condizionale
Se A e B sono due eventi dello spazio campionario S, si definisce probabilità di A
dato B, P(A|B):
P( A | B) 
P( A  B)
P( B)
S
B
A
AB
a) Lo spazio dell’evento B diviene il nuovo spazio campionario
b) Deriva che P(A|B)+P(A|B)=1.
17
Regola della moltiplicazione: dalla definizione di probabilità condizionale segue che:
P( A  B)  P( B) * P( A | B) 
 P( A) * P( B | A)
Se il verificarsi di B non condiziona la probabilità del verificarsi di A segue che:
P( A  B)  P( A) * P( B)
18
Esempio:
Calcolare la probabilità di estrarre da un urna consecutivamente due palline rosse,
sapendo che l’urna contiene 3 rosse, 2 nere, 1 verde, e l’estrazione è senza
reimbussolamento.
B= estrazione I pallina rossa
A= estrazione II pallina rossa
P(AB)=P(B)*P(A|B)
P(B)=3/6
P(A|B)=2/5
P(AB)=3/6*2/5=1/5
Se l’estrazione fosse con reimbussolamento:
P(A|B)=P(A)=P(B)=3/6
P(AB)=3/6*3/6=1/4
Osservazione: Se due eventi A e B di S sono indipendenti, allora:
P(A|B)=P(A|B)=P(A)