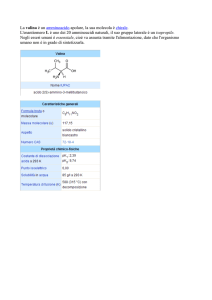
Elementi di fisica molecolare
16 La struttura delle molecole biatomiche
Una soddisfacente descrizione microscopica delle molecole deve rendere
ragione delle cause che promuovono l'aggregazione degli atomi e delle leggi che la
regolano, così come delle caratteristiche delle molecole e della natura ed intensità dei
legami. L'applicazione alle molecole della meccanica quantistica e dei concetti
sviluppati per gli atomi ha in effetti consentito una soddisfacente realizzazione di
questi obiettivi, fornendo una giustificazione indipendente di quei postulati, a
carattere piuttosto indefinito, introdotti nel linguaggio fenomenologico della chimica.
L'equazione di Schrödinger per la molecola contiene, in linea di principio,
tutte le informazioni necessarie; poichè è tuttavia impossibile una soluzione
strettamente matematica di tale equazione, si perviene ai risultati desiderati attraverso
ipotesi semplificatrici e approssimazioni di carattere fisico, che devono essere sorrette
dalla verifica sperimentale.
2.1 La separazione di Born-Oppenheimer
La più importante approssimazione di carattere generale riposa sulla disparità
della massa, e quindi di velocità, dei nuclei e degli elettroni. Tale disparità fa sì che
nel tempo in cui i nuclei variano apprezzabilmente la loro disposizione relativa (per i
moti di oscillazione e di rotazione) ogni elettrone, muovendosi molto più
velocemente, possa occupare molte volte la serie di posizioni che costituiscono
l'orbitale molecolare. Di conseguenza, nel descrivere la struttura elettronica si
possono considerare i nuclei fissi; d'altra parte i moti vibrazionali o rotazionali di
questi ultimi si possono ritenere, in prima approssimazione, indipendenti dal moto
degli elettroni. Questa approssimazione è sostenuta, dal punto di vista sperimentale,
dalla struttura dei livelli di energia delle molecole: gli spettri cadono, infatti, in tre
ben separati intervalli di lunghezza d'onda in corrispondenza delle transizioni tra
diversi tipi degli stati quantici (spettri elettronici nel VIS e nell'UV, spettri
vibrazionali nell'IR vicino, e spettri rotazionali nell'IR lontano).
Senza prendere in considerazione le interazioni magnetiche, l'equazione di
Schrödinger per una molecola si scrive:
ŠX/ Z/8 Z// X8 Z88 ‹<Ð<ß V Ñ œ IX <Ð<ß V Ñ
Ð2.1Ñ
dove i vari termini rappresentano, rispettivamente
X/ ´ !3
h#
#7
X8 ´ !!
f#3
h#
#Q!
Z/8 ´ !!ß3 ^<!!/3
Z// ´ !34
f!#
#
/#
<34
Z88 ´ !! "
energia cinetica degli elettroni
Ð2.2Ñ
energia cinetica dei nuclei
Ð2.3Ñ
attrazione coulombiana per gli elettroni
repulsione elettrostatica tra gli elettroni
^! ^" / #
V!"
repulsione elettrostatica tra i nuclei
Ð2.4Ñ
Ð2.5Ñ
Ð2.6Ñ
con
<!3 ´ l V! <3 là
Anno accademico 2011/2012
V!" ´ l V! V" là
<34 ´ l <3 <4 l
1
Elementi di fisica molecolare
Con < e V abbiamo indicato l'insieme delle coordinate degli elettroni Ö<3 × e dei nuclei
ÖV! ×, rispettivamente.
La marcata separazione dei livelli di energia elettronici da quelli associati al
moto dei nuclei e la disparità di massa tra i nuclei ed elettroni suggeriscono di
considerare il moto elettronico indipendente da quello nucleare e di considerare il
sistema elettronico sempre in una situazione di equilibrio durante il (lento) moto dei
nuclei. Ovvero, il sistema elettronico seguirà adiabaticamente il cambiamento
spaziale delle posizioni dei nuclei, con una successione di stati di equilibrio descritti
da una autofunzione elettronica stazionaria </ Ð<ß V Ñ, soluzione di un'equazione di
Schrödinger stazionaria a nuclei fermi. Pertanto, potremo fattorizzare la funzione
d'onda
<Ð<ß V Ñ œ </ Ð<ß V Ñ98 ÐV Ñ
Ð2.7Ñ
dove 98 ÐV Ñ dipende solo dalle coordinate dei nuclei, mentre </ Ð<ß V Ñ descrive gli
stati elettronici in corrispondenza a una configurazione a nuclei fissi, individuata dalle
coordinate V , dalle quali </ dipende solo parametricamente. L'autofunzione così
fattorizzata è adatta a descrivere i moti elettronici e nucleari nell'ipotesi di reciproca
indipendenza.
Per quanto detto, la </ Ð<ß V Ñ sarà soluzione dell'equazione di Schrödinger
elettronica
ŠX/ Z/8 Z// ‹</ Ð<ß V Ñ œ I/ ÐV Ñ </ Ð<ß V Ñ
Ð2.8Ñ
con le coordinate V costanti. I termini X/ Z/8 Z// rappresentano l'hamiltoniana
L/ del sistema di elettroni in un potenziale a nuclei fissi, con autofunzione </ Ð<ß V Ñ e
autovalore I/ ÐV Ñ. Sostituendo la (2.7) nell'equazione generale e tenendo conto della
(2.8) e che l'operatore X8 agisce solo sulla funzione d'onda nucleare otteniamo:
ŠX8 Z88 I/ ÐV Ñ‹98 ÐV Ñ œ IX 98 ÐV Ñ
Ð2.9Ñ
I termini X8 Z88 I/ ÐV Ñ rappresentano l'hamiltoniana L8 del sistema dei nuclei,
con autofunzione 98 ÐV Ñ e autovalore IX . I nuclei si trovano, quindi, ad essere
sottoposti al potenziale efficace: Z/0 0 ´ Z88 I/ ÐV Ñ, somma del potenziale
repulsivo Z88 e di quello, attrattivo, elettronico rappresentato dall'autovalore
elettronico I/ ÐV Ñ.
L'equazione generale dà quindi luogo a due equazioni di Schrödinger separate,
per il sistema elettronico e per il sistema nucleare.
Per giungere a questo risultato abbiamo fatto operare l'operatore nucleare X8
solo sulla autofunzione 98 , trascurando quindi i due termini derivanti
dall'applicazione di X8 sul prodotto </ Ð<ß V Ñ98 ÐV Ñ: l'approssimazione di Born Oppenheimer consiste, appunto, nel ritenere solo il termine X8 98 ÐV Ñ nella (2.1)
quando si usa la (2.7).
Nella (2.9) compare come energia potenziale effettiva l'autovalore
dell'equazione elettronica: gli elettroni forniscono, quindi, un'energia potenziale per il
moto dei nuclei, mentre il movimento dei nuclei deforma continuamente
l'autofunzione degli elettroni (piuttosto che produrne bruschi cambiamenti). Per tale
motivo il termine I/ ÐV Ñ si suole chiamare contributo adiabatico dell'equazione per il
moto dei nuclei: fisicamente esso traduce, come si è detto, il fatto che, fissato uno
Anno accademico 2011/2012
2
Elementi di fisica molecolare
stato elettronico della molecola, nel corso del moto dei nuclei si verificano variazioni
nell'energia degli elettroni, senza che vari peraltro lo stato.
Da quanto detto per l'eq.(2.9) segue che le autofunzioni nucleari dipenderanno
anche dai numeri quantici elettronici.
2.2 Moti di rotazione e di vibrazione dei nuclei
Nello spirito della separazione di Born-Oppenheimer, dopo aver, quindi,
studiata la struttura elettronica delle molecole, prendiamo ora in considerazione il
comportamento dinamico dei nuclei.
Nell'ambito della separazione di Born-Oppenheimer l'equazione di
Schrödinger per i nuclei (2.9) descrive il moto di rotazione della molecola nello
spazio e i moti di oscillazione dei nuclei attorno alle posizioni di equilibrio. Gli spettri
rotazionali e vibrazionali indicano che le corrispondenti frequenze sono notevolmente
diverse e che i moti hanno quindi carattere quasi additivo. Pertanto è possibile in
prima approssimazione, considerare separatamente i moti di rotazione da quelli di
vibrazione.
Studieremo dapprima la (2.9) e le sue soluzioni riferendoci a molecole
biatomiche nello stato fondamentale. Non considereremo pertanto alcune interazioni a
carattere magnetico che interessano i momenti angolari elettronici e nucleari; allo
stesso modo non considereremo esplicitamente l'interazione elettrica di quadrupolo
dei nuclei con i gradienti di campo dovuti agli elettroni. Le interazioni magnetiche ed
elettroniche tra i nuclei e gli elettroni di una molecola si manifestano in genere
attraverso una struttura fine delle righe di assorbimento rotazionale: con i recenti
progressi nella risoluzione sperimentale, sia nelle tecniche a microonde che
infrarosso, diviene possibile per questa via ottenere informazioni sulle funzioni d'onda
elettroniche nelle molecole.
L'equazione (2.9) nel caso di molecole biatomiche si riduce a
ŠX8 Z/0 0 ‹98 ÐV Ñ œ IX 98 ÐV Ñ
Ð2.12Ñ
con
X8 œ
h# #
h#
P#
fV œ
Ðf#V # # Ñ
#.
#.
h V
Ð2.13Ñ
avendo introdotto il vettore di posizione relativa nucleare V ´ V! V" , la massa
ridotta nucleare "/. ´ "/Q! + "/Q" (Figura 2.1), il momento angolare nucleare P,
e avendo posto
f#V ´ f#V
#
œfV œ
" `
`
ÐV #
Ñ ;
#
V `V
`V
P# œ h #
P#
h # V#
" `
`
"
`#
‘
Ð=38)
Ñ
=38) ` )
`)
=38# ) ` 9#
Ð2.14Ñ
Ð2.15Ñ
L'hamiltoniana L8 œ X8 Z/0 0 prende quindi l'espressione:
L8 œ
h# #
P#
fV Z/0 0 ÐVÑ
#.
#. V #
Ð2.16Ñ
Come abbiamo già accennato, la notevole differenza tra le regioni spettrali in cui
Anno accademico 2011/2012
3
Elementi di fisica molecolare
cadono le transizioni vibrazionali e quelle rotazionali ci porta a considerare in prima
approssimazione i moti di vibrazione e di rotazione come disaccoppiati. Le deviazioni
dai casi di vibrazione pura, ed armonica, e gli accoppiamenti vibro - rotazionali sono,
quindi, trattati perturbativamente.
Vediamo la forma di questi termini di perturbazione nell'operatore L8 . Se
indichiamo con V/ la posizione del minimo di potenziale efficace Z/0 0 ÐVÑ (Figura
2.2), possiamo sviluppare sia Z/0 0 ÐVÑ che V # in serie di potenze degli scostamenti,
supposti piccoli, B ´ V V/ , dalla posizione di equilibrio V/ . Avremo:
Z/0 0 ÐVÑ œ Z/0 0 ÐV/ Ñ Š
´
` Z/0 0
" ` # Z/0 0
‹ B Š
‹ B# ÞÞÞ
`V V/
`V # V/
#
" # " $
"
5B !B " B% ÞÞÞ
#
'
#%
Figura 2.1
Ð2.17Ñ
Figura 2.2
ove si è posto Z/0 0 ÐV/ Ñ œ !, assumendo così lo zero di Z/0 0 ÐV/ Ñ in corrispondenza
del minimo del potenziale, e si è tenuto conto dell'annullarsi della derivata prima di
Z/0 0 ÐV/ Ñ in V/ . Nella (2.17) 5 è una costante elastica che traduce la curvatura di
Z/0 0 ÐVÑ in V/ . Inoltre avremo:
"
"
#B $B#
µ
"
# ÞÞÞ‹
Š
V#
V/#
V/
V/
Ð2.18Ñ
Pertanto, sostituendo le (2.17) e (2.18) nella (2.16)
L8 œ
h# #
"
P#
fV 5B#
#.
#
#.V/#
P#
#B $B#
"
"
# ÞÞÞ‹ !B$ " B% ÞÞÞ
Š
#
#.V/
V/
V/
'
#%
Anno accademico 2011/2012
Ð2.19Ñ
4
Elementi di fisica molecolare
Poniamo
L@! ´
L<! ´
w
h# #
"
fV 5B#
#.
#
P#
#.V/#
L ´
Ð2.20Ñ
Ð2.21Ñ
P#
#B $B#
"
"
# ‹ !B$ " B%
Š
#
#.V/
V/
V/
'
#%
Ð2.22Ñ
Gli operatori L@! e L<! descrivono, rispettivamente, il moto di vibrazione armonica
dei nuclei e la rotazione "rigida" della molecola, indipendenti tra loro. L'operatore L w
descrive l'interazione tra questi moti e tiene conto dell'anarmonicità del potenziale e
della deformabilità della molecola. Il contributo di L w viene trattato
perturbativamente, dopo aver trovato le soluzioni dell'equazione "imperturbata":
L ! 98 ÐV Ñ ´ ÐL@! L<! Ñ 98 ÐV Ñ œ IX 98 ÐV Ñ
Ð2.23Ñ
Consideriamo soluzioni fattorizzate, ponendo:
98 ÐV Ñ ´
"
9@ ÐV Ñ 9< ÐHÑ
V
Ð2.24Ñ
Sostituendo la (2.24) nella (2.23) otteniamo
L@! 9@ ÐV ÑÎV ‘ œ I@! 9@ ÐV ÑÎV
Ð2.25Ñ
L<! 9< ÐHÑ œ I<! 9< ÐHÑ
Ð2.26Ñ
IX œ I@! I<!
Ð2.27Ñ
con
2.2.1 Moto di rotazione di una molecola biatomica rigida
Studiamo dapprima l'equazione di Schrödinger che descrive la rotazione rigida
della molecola:
P#
9< ÐHÑ œ I<! 9< ÐHÑ
#.V/#
Ð2.28Ñ
Come sappiamo, gli autovalori di P# sono N ÐN "Ñh # e quelli di PD sono QN h , e le
autofunzioni sono le armoniche sferiche ]N ßQJ ÐHÑ. Avremo, perciò:
9< ÐHÑ œ ]N ßQJ ÐHÑ
I<! œ
N ÐN "Ñh #
´ F2N ÐN "Ñ
#.V/#
Ð2.29Ñ
Ð2.30Ñ
dove si è introdotta la "costante rotazionale" F :
Anno accademico 2011/2012
5
Elementi di fisica molecolare
F´
h
%1 M
Ð2.31Ñ
con M ´ .V/# momento d'inerzia della molecola. La (2.30) può anche essere fatta
discendere dall'espressione classica per l'energia cinetica I œ P# /#M , dove P è il
modulo del momento angolare e M il momento di inerzia rispetto all'asse di rotazione
(trascurando il piccolo contributo dovuto agli elettroni). I livelli di energia rotazionale
si presentano pertanto come una successione discreta; sono caratterizzati dai valori 0,
1, 2, ... del numero quantico rotazionale N , e sono degeneri in QJ (Figura 2.3). La
separazione tra livelli adiacenti è:
?IN "ßN œ #F2ÐN "Ñ
Ð2.32Ñ
Figura 2.3. Distribuzione
dei livelli rotazionali
di una molecola biatomica
rigida.
Come vedremo successivamente, le regole di selezione per transizioni di dipolo
elettrico sono
?N œ „ " à ?QN œ !ß „ "
Ð2.33Ñ
e, inoltre, la molecola deve possedere un momento di dipolo elettrico permanente H!
per poter avere uno spettro di rotazione pura. Ciò si verifica per le molecole
(biatomiche) eteronucleari, ma non per quelle omonucleari. Molecole simmetriche
come R# e S# non possono, quindi, nè assorbire nè emettere radiazione e.m. a seguito
di transizioni tra livelli rotazionali puri.
Per la (2.33) le frequenze di assorbimento (o di emissione) sono, perciò,
(?N œ "):
/ œ #FÐN "Ñ
Ð2.34Ñ
ovvero crescono linearmente con N (l'energia cresce come N # ). Lo spettro risulta,
pertanto, composto da una serie di righe equispaziate, con separazione uguale al
doppio della costante rotazionale:
l?/ l œ #F
Anno accademico 2011/2012
Ð2.35Ñ
6
Elementi di fisica molecolare
La misura dell'intervallo di frequenza fra righe successive permette di conoscere F ,
da cui si ricava il momento d'inerzia M , e, quindi, dato che le masse sono note, si può
determinare la distanza di equilibrio dei nuclei. La precisione può raggiungere "!$
Å. La prima riga della transizione 0-1 nello spettro rotazionale della molecola CO ha
µ
/ œ $Þ)%#$& cm" , pari a "Þ"& "!"" LD , da cui segue: FGS œ "Þ*# -7" µ .'
"!"! LD e V/GS µ "Þ"$ Å . Le frequenze rotazionali cadono nella regione delle
microonde ("!" ƒ "! -7" ) o del lontano infrarosso ("! ƒ &!! -7" ). La Figura
2.4 mostra lo spettro di assorbimento rotazionale della molecola LG6. Si noti la
costanza della separazione tra le varie righe successive.
Figura 2.4. Spettro assorbimento dell’HCl gassoso
La conoscenza dei momenti di inerzia per molecole formate da isotopi diversi
permette di confrontare le masse di questi con una notevole accuratezza, che in casi
favorevoli è paragonabile a quella ottenibile con gli spettrografi di massa.
Notiamo infine che per la (2.29) la probabilità che l'asse molecolare cada
nell'angolo solido unitario attorno alla direzione individuata da ) e 9 risulta
lQ l
:N ßQN Ð) Ñ œ R lTN
Ð-9=)Ñl#
Ð2.36Ñ
con R fattore di normalizzazione e T polinomio associato di Legendre. Nello stato
fondamentale è T!! œ "/%1: in accordo al principio di indeterminazione, essendo
perfettamente definita l'energia, risulta completamente indeterminata la orientazione
dell'asse molecolare. In generale, la probabilità di presenza dell'asse si presenta come
quella descritta per l'elettrone nell'atomo di L negli stati =,:,. , .... Per gli stati
lQ l œ N si tende, al crescere di N , alla probabilità di orientazione prevedibile
classicamente, con il valore più probabile per ) œ 1Î#.
2.2.1.1 Intensità delle righe rotazionali
L'intensità delle righe di uno spettro di emissione rotazionale è determinata dal
numero 8N ÐX Ñ di molecole che, all'equilibrio termico, si trovano nello N -esimo
livello. Come sappiamo, la legge di distribuzione di Boltzmann fornisce il rapporto
fra il numero di molecole presenti in due stati N w e N :
8N w
1N w
IN w IN
œ
/B:Š
‹
8N
1N
5X
Anno accademico 2011/2012
Ð2.37Ñ
7
Elementi di fisica molecolare
dove 1N indica il fattore di degenerazione del livello energetico N (cioè il numero di
stati quantici degeneri relativi a IN ). I livelli rotazionali sono, in realtà, #N " volte
degeneri, poiché gli stati con QN œ !ß „ ", „ #ß ÞÞÞß „ N , corrispondenti alle #N "
orientazioni di P, hanno la stessa energia. Per N w œ N e N œ !, la (2.37) diventa:
8N œ 8! Ð#N "Ñ /B:Š
IN I!
‹
5X
Ð2.38Ñ
Figura 2.5. Distribuzione
dell’intensità nello
spettro rotazionale di una
molecola biatomica rigida.
La distribuzione 8ÐN Ñ è indicata qualitativamente nella Figura 2.5. L'occupazione dei
livelli cresce inizialmente in modo lineare con N ; ben presto, però, il fattore
esponenziale interviene a ridurre la popolazione, e per alti valori di N 1'andamento è
del tipo /B: Ð +N # ). Nel caso della molecola di LF< a temperatura ambiente il
valore massimo di N è N œ $, con 8$ Î8! ~ %, mentre per N œ * si ha 89 Î8! ~ ½ .
Dalla (2.38) segue facilmente che il numero quantico rotazionale N7+B
corrispondente alla riga più intensa è l'intero più vicino a !Þ&* X ÐOÑÎF Ð-7" Ñ‘,
mentre la frequenza del massimo dell'inviluppo della banda rotazionale misurata
relativamente all'origine della banda è /7+B Ð-7" Ñ ~ "Þ") ÐFX ѽ .
2.2.2 Moto di vibrazione di una molecola biatomica
Analizziamo ora i moti che comportano una variazione della distanza nucleo nucleo in una molecola biatomica. L'equazione (2.25) diventa:
Š
h# #
"
fV 5B# ‹9@ ÐV ÑÎV ‘ œ I@! 9@ ÐV ÑÎV
#.
#
Ð2.44Ñ
ovvero
Š
h # .#
" #
5B ‹9@ œ I@! 9@
#
#. .B
#
Ð2.45Ñ
Posto
0 ´ !B à
!´Š
.5 ¼
‹ à
h#
-´
#I@!
à
h= !
= ! ´ È5Î.
Ð2.46Ñ
la (2.45) diventa:
. # 9@
Ð- 0# Ñ9@ œ !
. 0#
Anno accademico 2011/2012
Ð2.47Ñ
8
Elementi di fisica molecolare
che, a meno di differenti condizioni al contorno (il cui effetto può essere trascurato)
costituisce l'equazione di Schrödinger per l'oscillatore armonico. Le autofunzioni e gli
autovalori per l'energia di vibrazione risultano pertanto
#
9@ ÐBÑ œ R@ /!B L@ Ð!BÑ
"
I@! œ Ð@ Ñh=!
#
Ð2.48Ñ
Ð2.49Ñ
dove: =! rappresenta la frequenza propria di un oscillatore classico di massa 7 e di
costante di forza 5 ; @ è il numero quantico vibrazionale e prende i valori interi !, ", #,
... I livelli energetici vibrazionali (2.49) sono equispaziati (Figura 2.6) con
separazione uguale a h = ! . Per @ œ ! è I@! œ ½h = ! : l'energia dello stato vibrazionale
fondamentale non è zero, bensì vale ½h= ! . La molecola non assume mai, quindi, il
valore corrispondente al minimo della curva dell'energia potenziale: la differenza
dell'energia tra questo minimo e lo stato vibrazionale fondamentale si chiama energia
di zero di vibrazione. Questa situazione è richiesta dal principio di indeterminazione:
se in corrispondenza del minimo la molecola fosse ferma, avremmo la distanza
internucleare fissata (?B œ !) e la quantità di moto nulla (?: œ !), in violazione del
principio di Heisenberg.
Figura 2.6. Livelli energetici vibrazionali
di una molecola biatomica nel caso di
potenziale armonico.
Nella molecola di NaCl la separazione h= ! è uguale a !Þ!% /Z , mentre
l'energia di dissociazione è " /Z : vi sono circa #5 livelli vibrazionali nella buca di
potenziale (supposto armonico). Nella Figura 2.7 sono schematicamente riportate le
autofunzioni vibrazionali (polinomi di Hermite-Gauss) corrispondenti alle (2.48). Le
funzioni d'onda hanno la stessa parità di @. Nello stato fondamentale la probabilità di
presenza l9@œ! ÐBÑl# è massimo per B œ ! (V œ V/ ). Al crescere di @ cresce la
probabilità di trovare la molecola nella situazione di elongazione massima, come
prevedibile per un oscillatore classico. Esiste peraltro una probabilità finita di trovare
l'oscillatore al di là dei limiti di oscillazione classica. Transizioni tra gli stati
vibrazionali richiedono, in genere, radiazione e.m. dell'infrarosso (da circa "!! -7" a
circa %!!! -7" ). Le transizioni di dipolo elettrico tra stati vibrazionali sono regolate
dalla regola di selezione:
?@ œ „ "
Ð2.50Ñ
come vedremo in seguito, ovvero sono possibili solo le transizioni tra stati adiacenti.
Anno accademico 2011/2012
9
Elementi di fisica molecolare
Figura 2.7. Diagramma di alcune
autofunzioni vibrazionali.
La (2.50) dà quindi le righe di assorbimento fondamentali, che coincidono
tutte con la frequenza fondamentale =! Î#1. La frequenza di assorbimento permette di
ricavare la costante di forza 5 , e fornisce quindi informazioni sulle curve dell'energia
della molecola. Al 1° ordine, la probabilità di transizione dipende dal prodotto
Š
.H
Ø@w lB l@Ù
‹
.B Bœ!
Ne segue che gli spettri vibrazionali possono essere osservati solo se la molecola,
supposta non ruotante e disposta lungo l'asse B, ha un momento di dipolo elettronico
non nullo e variabile con la separazione internucleare, ovvero solo in molecole
eteronucleari. Inoltre, a causa del fattore (. H /.B)! , una molecola con un momento H
relativamente piccolo può ancora avere una derivata (. H /.B)Bœ! grande e, viceversa,
una molecola con grande momento di dipolo può avere un piccolo valore della
derivata del momento se il momento di dipolo è vicino al suo massimo valore per
V œ V/ . Ad esempio, la molecola di CO, che ha un momento di soli !Þ"" H/,C/,
possiede una grande derivata di H, ed è perciò uno dei più forti assorbimenti IR noti.
Il termine quadratico nello sviluppo in serie di Taylor di HÐBÑ conduce ad
elementi di matrice non nulli solo se ?@ œ „ #, ma corrispondentemente assai
minori ai termini lineari. Si hanno, così, righe di assorbimento di overtone, assai più
deboli, però, delle fondamentali (?@ œ „ "). Ricordiamo che le frequenze
vibrazionali cadono nella regione spettrale dell'infrarosso, !Þ) - 300 micron, per la
maggior parte delle molecole.
L'intensità di ogni componente spettrale risultante dalla transizione @ Ä @ "
è determinata anche dal numero R@ di molecole nel livello @-esimo. Per @ œ 1 si ha
h =!
R" œ R / 5X
Ð2.51Ñ
e poichè per la maggior parte delle molecole h=! è dell'ordine di 0.1 /Z (!Þ$( /Z per
LG6, !Þ!% /Z per R +G6) ne segue che a temperatura ambiente (5X µ #Þ&) "!#
/Z ) gran parte delle molecole si trovano nello stato vibrazionale fondamentale: la
riga di assorbimento è conseguente alla transizione ! Ä ".
È interessante notare come sia possibile ottenere l'evidenza sperimentale
dell'energia del punto zero di un oscillatore. Nel caso, ad esempio, dei tre isotopi L# ,
LH, H# , la curva dell'energia potenziale Z/0 0 ÐVÑ è identica essendo le forze
elettriche in gioco esattamente uguali. Se l'energia di zero fosse nulla, tutte le
molecole avrebbero la stessa energia di dissociazione Z.3== . Si trova, invece, che
l'energia di dissociazione è diversa per le tre molecole, e corrisponde esattamente ai
Anno accademico 2011/2012
10
Elementi di fisica molecolare
valori previsti Z! ½h=! , tenendo conto della diversità delle masse ridotte che
entrano nell'espressione di =! data dalla (2.26) (Figura 2.8).
Figura 2.8
2.2.4 Moti roto-vibrazionali
Finora abbiamo considerato separatamente i moti rotazionali e vibrazionali di
una molecola biatomica. A causa della piccola energia necessaria per eccitare uno
stato rotazionale, la molecola compirà, in genere, un moto oscillatorio-rotatorio, con
un periodo di rotazione che è "!# ƒ "!$ volte maggiore di quello di oscillazione.
Questi due moti risulteranno accoppiati tra loro, come accade nel caso di due pendoli
connessi da un'asta non perfettamente rigida, ed invece di osservare la frequenza
vibrazionale pura /! , vedremo le due frequenze /! „ /N molto vicine a /! (essendo
/! ¦ /N ). A causa della distribuzione (2.38) di /N , lo spettro apparirà a bassa
risoluzione come quello indicato in Figura 2.10. Si noti che manca la riga a / œ /! .
Combinando i risultati dei paragrafi precedenti possiamo determinare lo spettro vibrorotazionale di una molecola biatomica. L'energia I@ßN dei livelli energetici di
oscillazione e di vibrazione è data da (Figura 2.11):
"
I@ßN œ Ð@ Ñh =! F2N ÐN "Ñ
#
Ð2.56Ñ
In una transizione tra un livello con numeri quantici @w , N w e un altro livello @, N la
frequenza emessa o assorbita sarà:
/ œ Ð@w @Ñ /! F N w ÐN w "Ñ N ÐN "Ñ‘
Ð2.57Ñ
La banda "fondamentale" si ha per @w @ œ ", per cui
/ œ /! F N w ÐN w "Ñ N ÐN "Ñ‘
Ð2.58Ñ
Tenendo conto della regola di selezione ? N ´ N w N œ „ ", si ha:
/ œ /! FÐN "Ñ
/ œ /! #F J
con N œ !ß "ß #ß ÞÞÞ (Ramo V , ?N œ ")
Ð2.59Ñ
con N œ "ß #ß ÞÞÞ (Ramo T , ?N œ ")
Ð2.60Ñ
Queste formule danno due successioni di righe equidistanti in frequenza (?/ œ #F )
che si estendono una da un lato e l'altra dall'altro della frequenza fondamentale /! e
sono i cosiddetti rami R e P della banda. La frequenza fondamentale non appare in
nessuna delle due ed è perciò marcata da una linea mancante (riga zero, null line).
Questo si intuisce facilmente perchè una pura alterazione nell'oscillazione non
potrebbe conservare il momento angolare nel processo di assorbimento (o di
Anno accademico 2011/2012
11
Elementi di fisica molecolare
emissione) della radiazione. Perciò, le transizioni vibrazionali sono accompagnate da
un cambiamento nello stato rotazionale.
L'uno e l'altro ramo della banda mostrano un caratteristico massimo
nell'intensità delle righe che riflette la distribuzione statistica dei numeri quantici di
rotazione.
Ramo R
Ramo
RamoRP
Ramo P
Figura 2.10
Si osservi che è possibile avere ?N œ ! con ?@ œ „ " solo in certi casi
eccezionali in cui la molecola possiede un momento angolare attorno all'asse
internucleare, come quando il momento angolare elettronico della molecola è diverso
da zero. In questo caso lo spettro contiene anche la frequenza vibrazionale
fondamentale /! , che prende il nome di ramo zero o ramo Q (Figura 2.12).
La Figura 2.13 mostra il diagramma dei livelli energetici roto-vibrazionali
dell'HCl e il corrispondente spettro; la Figura 2.14 mostra lo stesso spettro a più alta
risoluzione. La Figura 2.15 mostra poi lo spettro vibro-rotazionale della molecola di
CO ad alta risoluzione.
In realtà, lo spettro ideale di Figura 2.12 con le righe equispaziate non si
osserva: le righe nei rami P e R non si susseguono a distanza costante, e il ramo Q,
quando si presenta, non è una riga singola, ma mostra una struttura fine. La ragione di
ciò risiede nel fatto che le dimensioni, e quindi il momento d'inerzia, della molecola
non sono le stesse negli stati iniziali e finale della transizione vibrazionale.
Indichiamo con F w e F i valori della costante di rotazione per i livelli considerati.
Quando lo stato rotazionale diminuisce di una unità, cioè N w œ N " (?N œ ")
(ramo P) le frequenze di transizione sono espresse da
/T ÐN Ñ œ /! ÐF w FÑJ ÐF w FÑN #
con N œ "ß #ß ÞÞÞ (Ramo T ) Ð2.61Ñ
Quando la stato rotazionale aumenta di una unità, cioè N w œ N +" (?N œ +", ramo
R), si ha
/V ÐN Ñ œ /! ÐF w FÑJw ÐF w FÑN
w
#
con N w œ "ß #ß ÞÞÞ (Ramo V) Ð2.62Ñ
Quando si verificano, transizioni con N w œ N (?N œ !) danno luogo al ramo Q, con
frequenza
/U ÐN Ñ œ /V ÐN Ñ œ /! ÐF w FÑJ ÐF w con
FÑN
N #œ "ß #ß ÞÞÞ (Ramo U) Ð2.63Ñ
Anno accademico 2011/2012
12
Elementi di fisica molecolare
Ramo R
Ramo Q
Figura 2.12
Ramo P
ν
Figura 2.13
Figura 2.11
In queste formule, il livello inferiore ha sempre momento angolare N , mentre il livello
superiore ha momento angolare N ",N , o N " per i rami P, Q e R,
rispettivamente.
A differenza degli spettri di rotazione pura e di rotazione - oscillazione, qui i
termini quadratici in N non si eliminano dall'espressione di / (a causa del fatto che è
F w Á F ), e questo fa sì che le righe, invece di essere equidistanti, si infittiscono in
certi punti. Nella Figura 2.16 si riportano i vari rami separatamente, avendo supposto
F w F , e lo spettro completo. Il punto in cui la separazione del ramo (R in questo
caso) decresce a zero è chiamato testa della banda.
Le due equazioni per /V e /T possono essere combinate nella seguente
equazione:
/T ßV ÐN Ñ ´ /: ÐN Ñ œ /! ÐF w FÑ: ÐF w FÑ:#
con : œ „ "ß „ #ß ÞÞÞÐ2.64Ñ
dove valori positivi di : corrispondono al ramo V (?N œ +"), mentre valori negativi
di : corrispondono al ramo T (?N œ ").
Anno accademico 2011/2012
13
Elementi di fisica molecolare
Figura 2.14. Spettro di assorbimento dell’HCl.
I doppi picchi sono dovuti alla presenza dei due
isotopi 35Cl e 37Cl. La costante rotazionale risulta B =
1.31 103eV.
Figura 2.15. Banda fondamentale del CO. I doppi
picchi sono dovuti a tracce dell’isotopo 13CO.
Anche l'equazione (2.'$) può essere riscritta come:
/U ÐN Ñ œ /! ÐF w FÑ; ÐF w FÑ; #
Figura 2.16
con ; œ "ß #ß ÞÞÞ Ð2.65Ñ
Figura 2.17
Ciascuna di queste equazioni rappresenta una parabola (parabola di Fortrat). Il mezzo
più comodo per mettere in risalto le caratteristiche degli spettri vibro - rotazionali è il
cosiddetto diagramma di Fortrat, dove in ascisse si riportano le frequenze /T ßV,Q e in
ordinate i valori (positivi e negativi) di : e (solo positivi) di ; . I vari rami formano
archi di parabola, che nel caso T , V si raccordano fra loro (per : œ !, non permesso)
(Figura 2.17). Siccome le righe corrispondono ai punti delle parabole che hanno
ordinata intera (o eventualmente semi-intera) si ha un infittimento delle righe verso i
vertici delle parabole (teste delle bande). Che le bande si diradino verso le /
decrescenti, come si è supposto nel tracciare il diagramma di Figura 2.17, oppure
verso le / crescenti, dipende dal segno del coefficiente del termine quadratico delle
formule (2.61,62,63) (tale termine è lo stesso in tutte e tre, ossia dipende dal segno
della differenza F w F ). Si incontrano tutti e due i casi e perciò si hanno bande
sfumate verso il rosso e bande sfumate verso il violetto, ma per ogni sistema di bande,
Anno accademico 2011/2012
14
Elementi di fisica molecolare
cioè per tutte quelle bande che corrispondono ad un dato salto elettronico, la
sfumatura è, di regola, sempre rivolta nello stesso senso. Una proprietà utile del
diagramma di Fortrat è che la testa della banda corrisponde al vertice della parabola
T ,V .
2.3 Moti rotovibrazionali con cambiamento dello stato elettronico
Gli stati rotazionali e vibrazionali nelle molecole sono dovuti al moto dei
nuclei. Nei paragrafi precedenti abbiamo supposto la molecola nella configurazione
elettronica più bassa (fondamentale). Vi possono essere, anche, naturalmente, stati
elettronici eccitati, corrispondenti a configurazioni elettroniche differenti. Per
ciascuno di questi stati eccitati c'è una dipendenza diversa dell'energia della molecola
dalla sua separazione internucleare. Poichè gli atomi sono legati meno fortemente
negli stati eccitati, le corrispondenti curve dell'energia potenziale sono meno profonde
e più larghe, e la separazione di equilibrio V/ cresce al crescere dell'eccitazione
elettronica (Figura 2.19). La separazione fra stati elettronici diversi è di " "! /Z , e
le corrispondenti transizioni generano bande che cadono nel visibile e
nell'ultravioletto.
Trascurando le interazioni, l'energia totale di uno stato si può scrivere:
IX œ I/Ð1Ñ I@3, I<9>
Ð2.66Ñ
e la funzione d'onda completa è il prodotto di quella elettronica, di quella
vibrazionale, e di quella rotazionale. Nel caso di una molecola biatomica la variazione
di energia nel caso di una transizione tra stati elettronici risulta, per quanto abbiamo
visto in precedenza:
"
"
Ð#Ñ
Ð"Ñ
?I œ IX IX œ I/Ð1# Ñ I/Ð1" Ñ h =!# Ð@# Ñ h =!" Ð@" Ñ‘
#
#
F# 2N# ÐN# "Ñ F" 2N" ÐN" "Ñ‘
Ð2.67Ñ
Quanto alle regole di selezione, non ne esiste una definita per @ dato che i
livelli vibrazionali in gioco appartengono a curve potenziali molecolari
completamente differenti. Al più si può avere una certa distribuzione di probabilità
per le varie transizioni sulla quale torneremo più avanti. Per il numero quantico N si
ha ?N œ „ ", !. La possibilità N œ !, che era esclusa nei casi visti prima, deriva
dalla possibilità che il necessario cambiamento del momento angolare sia assicurato
da un cambiamento nel momento angolare degli elettroni. Perciò il caso ?N œ !.
viene a mancare se il momento angolare non è diverso almeno in uno dei due stati di
partenza e di arrivo.
Anno accademico 2011/2012
15
Elementi di fisica molecolare
Figura 2.19
È evidente che si possono realizzare transizioni in grande varietà, che
generano spettri assai complessi, che si presentano in forma di bande. Come nei casi
precedenti, una banda prende origine da tutte le transizioni nello stato di rotazione che
si possono associare a una data transizione nello stato elettronico e vibrazionale (cioè
tenendo fermi 1" e 1# , @" e @# ). Si ritrovano, così, le formule per i tre rami V , T , U
del paragrafo precedente, ma dove ora i coefficienti F dipendono, oltre che dallo stato
vibrazionale, anche da quello elettronico.
2.3.1 Principio di Franck-Condon
Secondo la (2.67) una transizione elettronica dovrebbe essere accompagnata
da un numero molto elevato di transizioni vibro-rotazionali, specialmente se
aggiungiamo alla (2.67) i termini anarmonici, che consentono transizioni con
@ œ „ #, „ $, ... In realtà il numero di bande vibro-rotazionali osservato negli spettri
molecolari VIS e UV è molto minore di quello previsto. Ciò fa pensare a qualche
effetto diverso dalle regole di selezione ?@ œ „ " (le regole per @ si applicano a
rigore solo per le bande vibro-rotazionali pure, ossia con 1" œ 1# ), che intervenga a
limitare le probabilità di transizione tra livelli vibrazionali appartenenti a stati
elettronici diversi. Si deve a Franck (anno ?) l'aver individuato il meccanismo fisico
che conduce al risultato osservato, in base a considerazioni di tipo classico.
Osserviamo innanzi tutto che una transizione elettronica avviene in un
intervallo di tempo molto piccolo rispetto al periodo di vibrazione, per cui la
separazione nucleare rimane praticamente la stessa durante la transizione elettronica,
e tale transizione può essere accuratamente rappresentata da una linea verticale
(distanza nucleare immutata) nel diagramma di Figura.2.21. Ciò deriva dal principio
di indeterminazione: se $I/ indica una tipica differenza di energia tra due livelli
Anno accademico 2011/2012
16
Elementi di fisica molecolare
elettronici, possiamo dire che il tempo in cui avviene questa transizione è il tempo $>/
in cui l'energia del sistema rimane incerta per la quantità $ I/ , per cui: $ I/ $ >/ µ h , e
posto $ I/ œ 2//
$ >/ µ
"
œ X/
//
ovvero, il tempo di transizione e dell'ordine del periodo ottico della radiazione emessa
nella transizione. Per transizioni VIS-UV è X/ ¶ "!"& =. Il periodo di vibrazione
7@ œ "Î/@ di una molecola è assai maggiore, dell'ordine di "!"$ =, per cui il rapporto
$ >/ Î7@ è tipicamente dell'ordine "!# ƒ "!$ .
Figura 2.20: spettro di emissione della molecola di AlO
Vediamo, adesso, di dare una valutazione della probabilità relativa delle varie
transizioni fra gli stati vibrazionali della molecola. Classicamente, se consideriamo
l'oscillazione di un pendolo, troviamo che esso trascorre la maggior parte del ciclo di
oscillazione vicino all'estremità del suo arco (dove la velocità si annulla) che non
nella zona centrale (dove la velocità è massima). La probabilità, quindi, che a un
istante scelto a caso l'ascissa si trovi ad avere un valore compreso tra B e B .B è
proporzionale all'inverso della velocità nel punto considerato
.B
.B
.T º Þ œ
B
=ÈB#! B#
Ð2.68Ñ
(dove B! indica l'ampiezza massima dell'oscillazione). La densità classica della
probabilità di presenza (normalizzata) è
T œ
"
1ÈB#! B#
Ð2.69Ñ
che mostra come la densità sia piccola al centro e grande (infinita) ai margini
dell'intervallo di oscillazione.
Qualcosa di simile succede anche trattando l'oscillatore con la meccanica
quantistica, specialmente per i numeri quantici non molto bassi, e in particolare per lo
stato fondamentale, in cui l<l# è una gaussiana con massimo al centro, e quindi non
ha nulla a che vedere con la distribuzione classica (corrispondente alla medesima
energia). La Fig.2.21 mostra alcuni livelli vibrazionali in ciascuno dei due stati
elettronici della molecola con sovrapposta la distribuzione T ÐBÑ œ l?@ ÐBÑl# data dalla
(2.48).Come si vede, al crescere di @, T ÐBÑ tende a diventare più grande agli estremi
dell'intervallo classico di oscillazione (questo comportamento si manifesta già per
@ œ $). Quando una molecola passa da uno stato elettronico (e di vibrazione) a un
altro, con che cambia anche la forma della curva che rappresenta l'energia potenziale
dei nuclei, si può quindi presumere che la transizione partirà dalla situazione più
Anno accademico 2011/2012
17
Elementi di fisica molecolare
probabile, riguardo alla vibrazione, e condurrà, senza che la distanza dei nuclei abbia
tempo di cambiare, verso un'altra situazione di massima probabilità (o, se si vuole,
verso un'altra situazione in cui l'energia cinetica dei nuclei rimane piccola). Nella
Figura 2.21 questo significa che la linea che rappresenta la transizione deve essere
verticale, come si è già osservato, e connettere per lo più due situazioni di massima
ampiezza, tanto nello stato di partenza che in quello di arrivo. Questo permette di
valutare per ogni numero quantico @w iniziale qual'è il più probabile numero quantico
di arrivo @. Per la funzione @w œ 0 Ð@Ñ si ottiene una curva parabolica (parabola di
Condon).
In ciò consiste il principio di Franck e Condon. Esso fu stabilito da Franck in
base a considerazioni classiche; successivamente Condon ne dette la corretta
impostazione quantistica. La formulazione quantistica del principio di Franck-Condon
consegue dalla determinazione delle regole di selezione per le possibili combinazioni
di 1, @ e N nella (2.67).
V=5
V=2
V=0
Figura 2.21, in cui si illustra il principio di FranckCondon che governa le transizioni elettroniche in una
molecola biatomica.
V=3
V=1
V=0
distanza interatomica
Anno accademico 2011/2012
18