5 - dieet

V.1
CAPITOLO V
I DISPOSITIVI A TRE TERMINALI: I TRANSISTORI AD EFFETTO DI CAMPO (FET)
5.1. - Premessa.
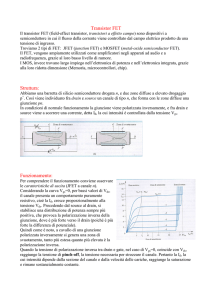
Abbiamo sinora studiato il funzionamento e le caratteristiche dei diodi a giunzione, che
sono dispositivi a due terminali. Al fine di realizzare una valvola a semiconduttore, un
dispositivo cioè che, attraverso l’accesso ad un terzo terminale, consenta di espletare
un’azione di controllo sulla corrente che fluisce tra gli altri due terminali, occorre la
disponibilità di una porta, così come schematizzato in Fig. 5.1.
porta
In campo idraulico, un esempio di valvola è
rappresentato da un comune rubinetto, in cui
I
VALVOLA
A
SEMICONDUTTORE
l’accesso alla manopola esterna (la porta) consente di
regolare il flusso d’acqua (equivalente alla corrente)
tra ingresso ed uscita del rubinetto (gli altri due
V
Fig. 5.1 – Modello di una
valvola a semiconduttore
terminali).
La
completa
attraverso
la
manopola
chiusura
esterna,
del
rubinetto,
impedisce
il
passaggio dell’acqua.
In realtà, in base a quanto già studiato, nel diodo a giunzione vi sarebbe la disponibilità
di una porta esterna che controlla la quantità di corrente che fluisce, in polarizzazione
inversa, tra i due terminali e cioè la temperatura. Si è visto infatti che una variazione di
temperatura produce una corrispondente variazione della corrente inversa. Questo tipo di
controllo è normalmente scartato nelle applicazioni dell’elettronica, a causa dei tempi lunghi
con cui si possono produrre le variazioni termiche.
Una tecnica senz’altro più accettabile sarebbe quella di illuminare la giunzione
polarizzata inversamente, dato che l’interazione della radiazione luminosa con la giunzione
produce una variazione della corrente inversa; anche se questa azione di controllo si può
produrre in tempi assai più ridotti rispetto a quelli richiesti dalle variazioni termiche, in realtà
tale tecnica, richiedendo l’integrazione di una sorgente luminosa molto vicina alla giunzione,
non viene praticata.
Le considerazioni sopra esposte spinsero i ricercatori a trovare una soluzione di tipo
elettronico e ciò ha portato a due tipi di soluzioni per la realizzazione di valvole elettroniche a
semiconduttore, costituite da:
a) i transistori ad effetto di campo (FET);
b) i transistori bipolari a giunzione (BJT).
(Febbraio 2010)
V.2
I primi furono realizzati per la prima volta nel 1952, anche se l’idea progettuale era stata
proposta nel 1930 a seguito delle esperienze fatte sul triodo a vuoto, valvola termoionica che
sfruttava un campo elettrico indotto nello spazio tra un elettrodo che emetteva elettroni ed un
secondo elettrodo che li raccoglieva per controllarne il flusso.
I secondi furono realizzati presso i Bell Telephone Laboratories (New Jersey, USA) nel
1947 da Bardeen e Brittain attraverso la scoperta dell’effetto transistorico, da “transfer
resistor”. In realtà, il premio Nobel per l’invenzione del transistor fu assegnato, oltre che ai
due ricercatori dei Bell Telephone Laboratories, anche a Schokley che alla Hughes
(California, USA) trovò lo stesso effetto nello stesso periodo.
5.2. – Classificazione dei FET.
I transistori ad effetto di campo o FET (Field Effect Transistor) sono dei dispositivi a
semiconduttore il cui funzionamento dipende dall’azione di controllo operata da un campo
elettrico sulla corrente che li attraversa. Più precisamente, l'intensità della corrente che
scorre nel semiconduttore tra due terminali (source e drain) viene controllata dalla tensione
applicata su un terzo terminale (gate). In base alla modalità con cui viene realizzato
l'elettrodo di controllo, i transistori ad effetto di campo in silicio possono raggrupparsi in tre
grandi famiglie:
1) FET a giunzione p-n o JFET (Junction Field Effect Transistor), in cui il gate è
realizzato con una giunzione p-n polarizzata inversamente;
2) FET a giunzione metallo-semiconduttore o MESFET (MEtal-Semiconductor Field
Effect Transistor), in cui il gate è realizzato con una giunzione rettificante metallosemiconduttore polarizzata inversamente;
3) FET
a
struttura
metallo-ossido-semiconduttore
o
MOSFET
(Metal-Oxide-
Semiconductor Field Effect Transistor), anche detti IGFET (Insulated Gate Field
Effect Transistor) per la loro struttura in cui il “gate” metallico è isolato dal
semiconduttore da un sottile film del dielettrico biossido di silicio; quest'ultimo è il
dispositivo maggiormente impiegato per la realizzazione di circuiti ad alto livello di
integrazione (VLSI), come i microprocessori e le memorie a semiconduttore.
Il grande successo dei MOSFET è anche dovuto alla realizzazione della tecnologia detta
CMOS, che ha consentito l’integrazione in maniera semplice di transistori MOS
complementari, di grande applicazione nell’elettronica digitale. Inoltre, come si vedrà nel
seguito, la tecnologia dei MOSFET consente con facilità di integrare sia dispositivi attivi, sia
condensatori e resistenze.
In breve, i transistori ad effetto di campo presentano le seguenti caratteristiche:
V.3
a) il loro funzionamento dipende dal flusso dei soli portatori maggioritari e per questo
motivo sono definiti dispositivi unipolari;
b) sono più semplici da realizzare rispetto ai transistori bipolari a giunzione (BJT) e nella
forma integrata occupano meno spazio;
c) presentano una elevata impedenza di ingresso (MΩ);
d) sono affetti da un “rumore” inferiore a quello presentato dai transistori a giunzione;
e) non presentano una tensione residua diversa da zero per correnti di drain prossime a
zero e quindi possono funzionare bene come interruttore.
Il principale svantaggio dei FET consiste nel fatto che il valore del prodotto
"amplificazione-larghezza di banda" per questi dispositivi è in genere più basso di quello che
tipicamente si ottiene nei transistori bipolari.
5.3. - Dispositivi JFET.
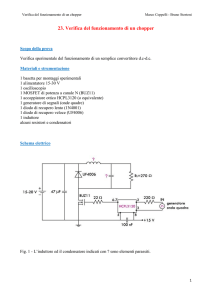
La struttura in sezione di un JFET “a canale n”, realizzato in tecnologia planare, è
illustrata in Fig. 5.2. Uno strato n è accresciuto epitassialmente su un substrato di tipo p. Una
ulteriore zona fortemente drogata di tipo p+ viene ottenuta per diffusione e in essa è
realizzato il contatto metallico corrispondente al terminale di gate (G). Al di fuori di tale zona
sono poste altre due zone drogate n+ corrispondenti ai contatti di source (S) e drain (D).
Una differenza di potenziale applicata tra i due contatti estremi provoca un flusso di
corrente che percorre il canale nel senso della sua lunghezza alla stessa stregua di un
resistore integrato. Si tratta di una corrente di portatori maggioritari e cioè, in questo caso, di
elettroni. Per la presenza della zona di svuotamento a ridosso della giunzione canalesubstrato, che nel funzionamento normale è per lo più polarizzata inversamente, il canale
stesso risulta isolato rispetto al substrato.
Source (VS)
S
Gate (VG)
Drain (VD)
G
D
IG
IS
p+
n+
zone di
svuotamento
c a n a l e
ID
n+
strato epitassiale
di tipo n
substrato di tipo p
Fig. 5.2 - Sezione di un JFET a canale n
V.4
Per il JFET mostrato in Fig. 5.2 si impiega la seguente nomenclatura convenzionale, valida
anche per tutti gli altri dispositivi FET:
-
il source S (emettitore - sorgente) è il terminale attraverso cui i portatori maggioritari
entrano nel dispositivo; la corrente che entra in S viene indicata con IS ;
-
il drain D (collettore - pozzo) è il terminale attraverso cui i portatori maggioritari escono
dal dispositivo; tra drain e source viene applicata una tensione VDS che nel seguito verrà
indicata brevemente come VD ; la corrente che entra in D viene indicata con ID ed è in
modulo praticamente coincidente con IS (a meno della corrente inversa della giunzione di
gate e se VD non è prossima al valore di rottura della giunzione drain-gate);
-
il canale, cioè la regione di tipo n attraverso la quale i portatori maggioritari si muovono
tra i due terminali di source e drain;
-
il gate G (base - porta) è il terminale di controllo che consente la variazione dello
spessore del canale; tra gate e source viene applicata una tensione VGS , indicata
brevemente come VG , in modo da polarizzare inversamente la giunzione p+-n; la
corrente (molto piccola o nulla) che entra in G viene indicata con IG .
D
D
JFET a
canale n
G
JFET a
canale p
G
S
S
Fig. 5.3 - Simboli circuitali dei dispositivi JFET
I simboli comunemente impiegati per rappresentare negli schemi circuitali i dispositivi
JFET, sia a canale n sia a canale p, sono riportati in Fig. 5.3. La freccia del terminale di gate
indica il verso della possibile corrente diretta sulla giunzione di gate. Riguardo i segni delle
tensioni e delle correnti, in un JFET a canale n si ha che ID e VD sono positive mentre VG , IS
e IG sono negative; in un JFET a canale p invece ID e VD sono negative mentre VG , IS e IG
sono positive (le tensioni, come detto, sono riferite al source).
I dispositivi di uso più comune sono i JFET a canale n, che vengono preferiti poiché
risultano più veloci dei dispositivi a canale p, nei quali la conduzione è affidata alle lacune.
Ciò risulta in quanto il tempo richiesto dai portatori per attraversare il canale è inversamente
proporzionale alla loro mobilità e come è noto, a parità di drogaggio, la mobilità degli elettroni
µn risulta maggiore di quella delle lacune µp .
Nel seguito ci si riferirà a dispositivi realizzati in silicio, tranne che diversamente
specificato.
V.5
5.4. – Funzionamento del JFET e sue caratteristiche corrente-tensione.
Nel seguito è riportato un procedimento per ricavare, con buona approssimazione,
l'espressione che lega la corrente di drain ID alla tensione di drain VD ed alla tensione di gate
VG in un JFET a canale n. Tale espressione permette di tracciare le curve caratteristiche di
uscita dei JFET (nel seguito indicate per brevità come caratteristiche ID - VD , riportate nel
paragrafo 5.5), in funzione della tensione di gate VG. Al fine di semplificare l'analisi, per il
JFET si considererà la struttura a barretta riportata in Fig. 5.4, simmetrica rispetto l’asse
orizzontale. Tale struttura idealizzata può pensarsi derivata da quella planare, rappresentata
in Fig.1, considerando come tratto utile soltanto la porzione di canale che in Fig. 5.2 è posta
immediatamente al di sotto del terminale di gate e supponendo che il gate ed il substrato di
tipo p siano collegati insieme. Nel modello considerato si supporrà inoltre che i drogaggi
delle due zone p siano eguali e che le giunzioni siano a gradino.
Gate (VG ≤ 0)
W
+
p
Drain (VD ≥ 0)
Source
canale n
2a
+
p
zone di
svuotamento
L
Fig. 5.4 - Struttura semplificata di un JFET a canale n per piccoli valori di VD
Con queste ipotesi, per il calcolo della "resistenza del canale" nel JFET, è possibile
considerare il canale stesso come un semplice parallelepipedo di silicio la cui resistenza è
R = L / (σ S), avendo indicato con L la lunghezza del canale, con S la sua sezione e con σ
la sua conducibilità. In tal caso, se 2a è la distanza tra le giunzioni metallurgiche che limitano
il canale, W la larghezza di ciascuna delle due zone di svuotamento e Z la dimensione del
dispositivo in direzione normale al piano del disegno, si può scrivere:
R=
1
L
σ 2 (a - W ) Z
dove W dipende dalla tensione di polarizzazione applicata al gate e la conducibilità σ vale
q µn ND , avendo indicato con ND il drogaggio del canale. Se il gate è polarizzato
V.6
inversamente e la giunzione p+-n è, come sempre avviene, asimmetrica e a gradino, si può
assumere che:
2ε
W =
q
s
1
(Φi − VG )
ND
Questo risulta vero fin quando il valore della tensione VD tra source e drain è inferiore
al volt, per cui si può trascurare la caduta di potenziale lungo il canale e considerare costante
il valore di W lungo tutto il canale. In tal caso si ottiene:
R=
1
L
q µn ND

2 εs 1
2 Z a −
( Φi − VG )

N
q
D





= R (VG )
Quindi, in presenza di una piccola tensione applicata VD la barretta di tipo n si comporta
come una semplice resistenza a semiconduttore nella quale, per assegnato valore di VG , la
corrente ID cresce linearmente con VD. Ne consegue che le caratteristiche ID - VD , al variare
di VG e per valori di VD prossimi allo zero, assumono la forma di una stella di rette passanti
per l’origine degli assi e ciascuna avente pendenza pari a 1/R (Fig. 5.5.a). In tale zona di
funzionamento il JFET si comporta come una resistenza il cui valore è controllabile da una
tensione: esso può essere pertanto impiegato, ad esempio, nei circuiti di controllo
automatico del guadagno (CAG) normalmente inseriti nel progetto dei circuiti amplificatori.
All'aumentare di VD cresce la corrente ID che scorre lungo il canale e, di conseguenza,
cresce anche la caduta resistiva di tensione distribuita tra source e drain. Per VG costante,
tale caduta di tensione contribuisce ad aumentare la polarizzazione inversa della giunzione
tra gate e canale, per cui la zona neutra del canale inizia a restringersi (vedi Fig. 5.5.a e
Fig. 5.5.b). L’influenza di VD comincia a farsi sentire quando il valore della VD stessa diventa
paragonabile al potenziale di barriera Φi tra gate e source. Inoltre, poiché il potenziale non
risulta costante lungo il canale (a causa appunto della caduta resistiva), il restringimento non
può risultare uniforme ma è più pronunciato nelle regioni vicine al drain. Quando ciò accade,
le caratteristiche ID - VD iniziano ad incurvarsi verso l’asse positivo delle ascisse, in quanto la
resistenza del canale cresce.
Aumentando ulteriormente VD , la corrente ID raggiunge un valore massimo che viene
indicato come IDsat e poi resta pressoché costante. Tale condizione, detta di "saturazione", si
verifica nelle caratteristiche quando la zona svuotata si è espansa a tal punto da annullare la
zona neutra del canale. Si suole dire che si è raggiunta la condizione di "strozzamento" del
canale (pinch-off) ed il valore della tensione di drain per il quale si raggiunge tale condizione
viene indicata con VDsat (Fig. 5.5.b).
V.7
ID
VG
VD > 0
VD
a)
VG
ID
IDsat
VD = VDsat
b)
VG
VDsat
VD
ID
IDsat
V’D > VDsat
c)
VDsat
V’D
VD
Fig. 5.5 - Funzionamento di un JFET in zona lineare (a),
in condizione di strozzamento (b), in zona di saturazione (c).
Naturalmente non è possibile che il canale si chiuda completamente e, di conseguenza,
che la corrente ID si riduca a zero. Se infatti si verificasse tale situazione, verrebbe meno
anche la caduta ohmica che consente di sostenere la necessaria polarizzazione inversa, per
cui il canale tenderebbe a riaprirsi. Aumentando la tensione VD oltre il valore VDsat , l'effetto
complessivo è allora un accorciamento della zona neutra del canale (visto che nella zona
strozzata la zona neutra ha già ampiezza nulla) ed un allungamento della zona strozzata,
restando però la ID pressoché costante e pari al valore di saturazione (Fig. 5.5.c). Questo
comportamento soddisfa sia la tendenza della zona di svuotamento ad espandersi
all'aumentare della polarizzazione inversa del canale, sia la necessità di avere una corrente
che scorra nel canale per mantenere la caduta ohmica. Tale fenomeno viene indicato con il
nome di “modulazione della lunghezza di canale”.
V.8
Gate (VG ≤ 0)
p+
Source
canale
n
dy
2a
Drain (VD ≥ 0)
W
p+
zone di
svuotamento
x
y y+dy
0
y
L
Fig. 5.6 - Modello di un JFET a canale n per VD < VDsat
Per ricavare l'espressione della caratteristica ID - VD, in condizioni prossime allo
strozzamento del canale, si può considerare una fetta di canale di lunghezza dy a distanza y
dall’inizio della barretta (Fig. 5.6). La caduta di tensione dV ai capi di dy è:
dV = ID dR
essendo:
dR =
dy
2 q µ n N D Z [ a - W ( y )]
La larghezza della zona di svuotamento W(y), variabile con la distanza y dal terminale di
source, si può esprimere come:
W (y ) =
2ε
s
q
1
[Φi − VG + V ( y )]
ND
dove V(y) rappresenta il termine additivo di potenziale, valutato alla sezione di coordinata y,
dovuto alla caduta di tensione lungo il canale fino a quella sezione.
Sostituendo, si giunge così all'espressione in forma differenziale:

2ε 1
s
[Φi − VG + V ( y )]
I D dy = 2 q µ n N D Z  a q ND



 dV


che va integrata lungo tutto il canale di lunghezza L. Si noti che il termine ID non varia con y.
Per ricavare in maniera semplice l'espressione di ID in funzione di VD a VG = cost, si può
ricorrere al seguente stratagemma. Partendo dall'espressione di W(y) ed elevandola al
quadrato, si ottiene:
W ( y )2 =
2ε
q
s
1
[Φi − VG + V ( y )]
ND
V.9
da cui, differenziando (si omette, per semplicità, l'indicazione della dipendenza da y):
2 W dW =
2ε
s
q
1
dV
ND
Utilizzando le espressioni di dV e dR sopra riportate, si giunge alla:
W q ND
dy
dW = I D
2 q µn ND Z [ a - W ]
ε
s
e quindi alla:
2
2 q 2 ND µn Z
[ a - W ] W dW = I D dy
ε
s
Integrando entrambi i membri tra 0 ed L lungo il canale, essendo ID costante con y, si ha:
2 q 2 N D 2 µ n Z WL
[ a - W ]W dW = I D L
εs
W0
∫
dove l'integrale presente a primo membro può essere agevolmente risolto.
Il risultato di tale integrazione è dato dall'espressione:
3


VD 2   Φi − VG + VD  2
 −

ID = IP 
−

V
3
V
P

 P
 

(1)
3 
 Φi − VG  2  



V
P
  


avendo posto:
IP =
Z µn q 2 ND 2 a3
εs L
e
VP =
q ND a 2
2 εs
L'espressione (1) della ID sopra ricavata vale per il JFET nella regione che va dall'inizio della
zona lineare fino al raggiungimento della saturazione. Quest’ultima situazione si ottiene
allorché la ID raggiunge il valore massimo IDsat . Per valori di VD superiori a VDsat
l’espressione appena trovata prevederebbe che la ID inizi a diminuire, come indicato dalla
curva tratteggiata in Fig. 5.5.c; ciò non si verifica in quanto sarebbe in contrasto con le
considerazioni relative al fenomeno della modulazione della lunghezza del canale.
La quantità VP viene detta "tensione di strozzamento" (pinch-off), pari alla tensione totale
di polarizzazione inversa (Φi -VG + VD) , sulla giunzione tra gate e canale, per la quale
W = a. Infatti, imponendo questa condizione nell'espressione di W(y), si ottiene:
a2 =
2 εs 1
[Φi − VG + VDsat ]
q ND
da cui:
VDsat
q a 2 ND
=
+ VG − Φi = VP + VG − Φi
2 εs
V . 10
Questo valore VDsat , sostituito nell'espressione di ID, permette di ricavare IDsat.
Esercizio:
Ricavare la (1) e dimostrare che, in tale espressione, il valore massimo di ID si
ottiene per VD = VDsat .
Esercizio:
Per un JFET al Si a canale n, con ND = 1016 cm– 3, NA = 1019 cm– 3, a = 1 µm,
L = 20 µm, Z = 100 µm e µn = 1350 cm2/(Vs), determinare:
a) la tensione di strozzamento VP;
b) la corrispondente corrente allo strozzamento con VG = 0.
(a. 7,6 V; b. 1,56 mA)
E' possibile infine ottenere l'espressione della ID per bassi valori di VD effettuando
qualche semplificazione all'espressione completa di ID sopra riportata. Infatti, per VD << Φi VG , i due addendi posti all'interno della parentesi quadra nell'espressione di ID possono
essere riscritti come:
3
3
3
3

 Φi − VG + VD  2  Φi − VG  2  Φi − VG  2 
VD
 − 
 = 
 (1+

) 2 − 1 ≅
VP
Φi − VG


 VP 
 VP  

3
1
 3 VD
 Φ − VG  2  3 VD
 1+
− 1 =
(Φi − VG ) 2
≅  i
3
 VP   2 Φi − VG  2 VP 2
da cui:
1 



1 
2


−
Φ
V
I


VD 2  3 VD
G
  VD
ID = IP 
(Φi − VG ) 2   = P 1-  i
−
3
  VP   VP  
VP 3  2 VP 2



quindi la ID è funzione lineare della VD. Sostituendo le espressioni di IP e VP ed effettuando il
rapporto
VD / ID
si
ottiene
l'espressione
precedentemente per bassi valori di VD.
della
resistenza
di
canale
R
ricavata
V . 11
5.5. – Caratteristiche corrente-tensione del JFET al variare di VG.
Ricapitolando, lungo ogni curva caratteristica per VG = cost (Fig. 5.7) si possono
osservare tre zone: una regione a comportamento resistivo per piccoli valori di VD , in cui ID è
direttamente proporzionale a VD e la curva è un segmento di retta (zona lineare); una zona di
transizione dove la curva inizia a piegarsi fino a diventare parallela all'asse delle ascisse; una
regione a corrente costante per valori elevati di VD in cui ID varia molto lentamente con VD
(zona di saturazione).
VDsat
ID
VG = 0V
10 mA
- 0,5V
- 1V
- 1,5V
- 2V
4V
20V
VD
Fig. 5.7 - Caratteristiche corrente-tensione di un JFET a canale n.
Si osservi che, nel caso del transistore bipolare a giunzione (BJT) e per motivi che
verranno chiariti in seguito, è il tratto iniziale delle caratteristiche (per bassi valori di tensione)
ad essere denominato “zona di saturazione“. Ciò può dar luogo a malintesi se non viene
specificato il tipo di dispositivo a cui si fa riferimento.
Per il JFET si può considerare una quarta zona di funzionamento, la zona di interdizione,
che si ha quando la VG è tale da svuotare completamente il canale. Infatti, se si applica al
gate una tensione VG via via maggiore e con polarità tale da aumentare la polarizzazione
inversa tra gate e canale, il fenomeno della strozzatura si manifesta per valori di VD sempre
più bassi e quindi più piccola sarà l’intensità massima della corrente di drain. Quando VG
raggiunge un valore indicato con VC (cut-off voltage), si giunge alla condizione per cui W = a
anche a bassissime tensioni di drain. In tal caso, la ID si mantiene pressoché nulla anche per
VD > 0 e la VC vale:
V . 12
VC = Φi −
q a 2 ND
2 εs
Si noti che nelle caratteristiche è talvolta presente, al di sopra della curva a VG = 0 V,
anche una curva a VG = +0,5 V, tensione alla quale la giunzione è polarizzata direttamente.
Occorre notare tuttavia che in tali condizioni la corrente attraverso la giunzione di gate sarà
molto piccola dato che una tensione di +0,5 V risulta, per le giunzioni p-n in silicio, al di sotto
della tensione di soglia Vγ .
ID
10 mA
VD > VDsat
- 4V
- 3V
- 2V
- 1V
0V
VG
Fig. 5.8 - Transcaratteristica di un JFET a canale n.
Quando è impiegato negli amplificatori, il JFET viene quasi sempre fatto funzionare nella
regione in cui si verifica lo strozzamento, detta anche “regione di pentodo”. Risulta allora
talvolta utile considerare la cosiddetta “transcaratteristica”, ottenuta tracciando l’andamento
della ID al variare di VG per un valore costante di VD (Fig. 5.8). Nell’ipotesi di considerare
perfettamente orizzontali i tratti delle caratteristiche di uscita relativi alla condizione di
strozzamento
e
di
considerare
solo
punti
appartenenti
a
tale
zona,
tutte
le
transcaratteristiche risultano sovrapposte ed è quindi possibile considerarne una soltanto.
Il JFET può anche essere impiegato in circuiti a commutazione. In tali applicazioni esso
viene fatto lavorare alternativamente o in interdizione, imponendo VG < VC in modo che ID sia
nulla, oppure in piena conduzione, impiegando una VG quanto più elevata possibile (purché
sempre inferiore alla Vγ.) in modo da portare il dispositivo a lavorare nella regione lineare a
bassi valori di VD . La resistenza di canale che si ottiene nelle condizioni di massima
V . 13
conduzione viene spesso indicato come RON ed è una delle grandezze caratteristiche del
JFET, in quanto rappresenta un indice della bontà del dispositivo nel funzionamento in
commutazione: minore è il suo valore, tanto meglio il JFET è in grado di approssimare un
interruttore chiuso. I valori tipici per la RON di un JFET sono compresi tra qualche decina ed
alcune migliaia di Ohm.
Per quanto riguarda la presenza di effetti capacitivi nel JFET, bisogna notare che in tale
dispositivo la concentrazione dei portatori lungo il canale è uniforme e la corrente è dovuta
soltanto al drift dei portatori maggioritari, non alla loro diffusione. Di conseguenza non si ha
accumulo di cariche, per cui non esiste capacità di diffusione. Gli unici effetti capacitivi sono
pertanto dovuti alle regioni di svuotamento o alle capacità interelettrodiche del contenitore
del dispositivo.
5.6. - Rottura del JFET.
Ad alti valori della tensione di drain VD è possibile considerare una quinta regione di
funzionamento, nella quale si ha la rottura della giunzione gate-drain, con conseguente forte
aumento della corrente ID . Infatti, la massima tensione che si può applicare tra due terminali
qualsiasi del JFET è la più bassa tensione che provoca il breakdown a valanga della
giunzione di gate. Si nota dalla Fig. 5.7 che, quando il gate è polarizzato inversamente, la
valanga si manifesta per valori di VD più bassi di quello per la curva a VG = 0. In tal caso,
infatti, la tensione di polarizzazione inversa del gate si aggiunge alla tensione applicata al
drain e quindi incrementa la tensione complessiva gate-drain. Quando si innesca la
condizione di rottura, la corrente di source IS non varia, visto che VD è costante, ma aumenta
notevolmente la corrente di drain ID , alla quale contribuisce, in tali condizioni, l’incremento
della corrente IG che assume valori confrontabili con le correnti IS ed ID .
5.6. - Polarizzazione del JFET.
Nell’elettronica analogica, per l’impiego nei circuiti amplificatori, il JFET viene
tipicamente polarizzato per mezzo di una rete di polarizzazione alimentata in continua, in un
punto di riposo all’interno della zona di saturazione, nella quale il dispositivo si comporta
come un generatore quasi ideale di corrente la cui intensità è funzione della tensione di gate.
Una volta scelto il punto di riposo (I*D , V*G , V*D) basandosi su considerazioni relative
all’amplificazione dello stadio, alla dinamica del segnale in uscita ed alla dissipazione
termica, si dovranno scegliere i valori dei componenti presenti nella rete di polarizzazione in
V . 14
modo da soddisfare, per quanto possibile, le specifiche richieste e le condizioni limite di
funzionamento fornite dal costruttore.
Il JFET è affetto da minori problemi di deriva termica rispetto, come si vedrà in seguito,
ai transistori a giunzione. Infatti all’aumentare della temperatura del dispositivo la corrente di
drain tende a diminuire, dato che la mobilità dei portatori nel canale diminuisce, per cui i
rischi di “fuga termica” sono ridotti. La dispersione delle caratteristiche è, invece, molto
pronunciata ed i costruttori in genere forniscono, oltre ai valori tipici dei parametri del
dispositivo, anche quelli minimi e massimi.
Come indicato in Fig. 5.4, per la corretta polarizzazione del JFET a canale n sono
necessari due generatori di tensione, il primo collegato tra gate e source in grado di imporre
una VG negativa, il secondo connesso nel circuito drain-source che dà luogo ad una VD
positiva. Al fine di impiegare un unico generatore di tensione per alimentare tutto il circuito, lo
schema di polarizzazione più comunemente impiegato è quello ad “autopolarizzazione”
riportato in Fig. 5.9.a, in cui la tensione VG negativa viene ottenuta sfruttando la caduta di
tensione sulla resistenza RS percorsa dalla corrente di drain. Nel seguito viene considerato
un JFET a canale n. Per quelli a canale p basta invertire il segno delle tensioni.
+
E
ID
E/(RS + RD)
RD
VD
VG
RG
a)
V*G
I*D
RS
b)
V*D
E
VD
Fig. 5.9 – (a) Circuito di autopolarizzazione per un JFET. (b) Caratteristiche di uscita
del JFET sulle quali è riportata la retta di carico.
Per un JFET a canale n, la tensione VG tra gate e source deve essere negativa. Inoltre la
corrente di gate IG si può considerare praticamente nulla, essendo pari alla corrente inversa
di un diodo. Per tale motivo, nonostante la presenza del resistore RG, in funzionamento
statico il potenziale del gate coincide con quello di massa. Con tale considerazione è
possibile applicare la legge di Kirchhoff alla maglia di ingresso, che fornisce:
V . 15
VG + RS ID = 0
dalla quale si ricava che la tensione VG tra gate e source è negativa e pari in modulo alla
caduta di tensione presente ai capi di RS . Applicando la legge di Kirchhoff alla maglia di
uscita, si ottiene invece la relazione che prende il nome di “retta di carico”, la cui espressione
è data da:
E = VD + ( RS + RD ) ID
Infatti, nel caso in cui si debba effettuare l’analisi del circuito e supponendo di possedere
in forma grafica le caratteristiche di uscita del dispositivo, l’equazione alla maglia di uscita
consente di tracciare su di esse la retta di carico (Fig. 5.9.b). L’equazione alla maglia di
ingresso permette invece di tracciare, sempre sulle caratteristiche di uscita, la curva di
polarizzazione (a causa della scarsa pendenza delle caratteristiche, è spesso possibile
determinare solo alcuni punti appartenenti a tale curva). L’intersezione di questa con la retta
di carico darà il punto di lavoro del dispositivo (I*D , V*G , V*D). Se invece si è in possesso
della transcaratteristica del dispositivo (Fig. 5.8), la curva di polarizzazione ID = f(VG) è
rappresentata su tale piano da una retta che interseca la transcaratteristica proprio nel punto
di lavoro.
Dovendo affrontare un problema di progetto è possibile risalire, a partire dalla
conoscenza di VG o di ID ed usando le caratteristiche di uscita in zona di saturazione, al
corrispondente valore ID o di VG , rispettivamente. Dall’equazione alla maglia di ingresso si
ricava il valore di RS . Essendo note la tensione di drain VD e quella di alimentazione E ,
dall’equazione alla maglia di uscita è possibile ricavare RD . Alternativamente, se è nota VD e
l’amplificazione di tensione dello stadio, che per il circuito di figura risulta prossima in valore
assoluto a RD / RS , si possono calcolare RD ed E.
Qualora non si possiedano le caratteristiche di uscita del dispositivo in forma grafica, è
possibile procedere in maniera analitica sfruttando l’espressione della caratteristica ID – VD
ricavata in precedenza. Spesso tuttavia si considera una semplice espressione verificata
sperimentalmente, valida in regime di saturazione, che esprime la corrente di drain in
funzione della tensione di gate e che approssima abbastanza bene la transcaratteristica di
Fig. 5.8:
I D = I DSS

V 
1 - G 
VC 

2
V . 16
dove IDSS rappresenta la corrente di drain per VG = 0, cioè con il gate cortocircuitato al
source. In tal caso i valori di IDSS e di VP vengono forniti dal costruttore. Nei problemi di
analisi l’espressione semplificata di ID può essere impiegata sostituendo – RS ID al posto di
VG, in base all’equazione alla maglia di ingresso. Si ottiene così una equazione di secondo
grado in ID che permette di determinarne il valore (si osservi che si ottengono due valori di ID
, ma soltanto uno verifica la condizione |VG| < |VP| ).
La semplice rete di autopolarizzazione riportata in Fig. 5.9.a presenta lo svantaggio che
il valore di RS è determinato dalla VG che si vuole applicare al gate. Tuttavia, come si vedrà
nel caso dei transistori a giunzione, se si vuole migliorare la stabilizzazione del punto di
riposo o aumentare la banda passante dello stadio amplificatore, bisogna elevare il valore
della RS . Per rendere la RS indipendente dalla VG si può utilizzare la rete “a quattro
resistenze” di Fig. 5.10.a, in cui la tensione di gate viene determinata anche dal partitore
R1 ; R2 .
E
E
RD
RD
R1
Req
VD
VD
VG
R2
+
Eeq
RS
a)
VG
RS
b)
Fig. 5.10 – (a) Circuito di polarizzazione a quattro resistenze per un JFET. (b) Lo stesso
circuito con generatore equivalente di Thevenin in ingresso.
Per analizzare il circuito conviene dapprima trasformare il partitore di ingresso nel
generatore equivalente secondo Thevenin, determinando Eeq ed Req (Fig. 5.10.b). Poiché il
partitore di ingresso non è caricato, essendo IG = 0, il potenziale a cui si trova il gate rispetto
massa è pari ad Eeq . L’equazione della maglia di ingresso allora diventa:
VG + RS ID = Eeq
mentre l’equazione della maglia d’uscita rimane:
E = VD + ( RS + RD ) ID
A partire da queste due equazioni è possibile applicare il metodo grafico o quello analitico
già descritti per il circuito di autopolarizzazione. Si osservi che, affinché il JFET funzioni
V . 17
correttamente, bisogna scegliere R1 ed R2 in modo che la tensione di gate risulti comunque
negativa, quindi Eeq < RS ID .
5.8. - Modello dinamico del JFET per piccoli segnali.
Per ricavare il modello equivalente lineare per piccoli segnali del JFET basta considerare
che, formalmente, è possibile esprimere la corrente di drain ID in funzione della tensione VG
e della tensione VD :
ID = f (VG ,VD)
Una volta fissato il punto di riposo del dispositivo (I*D , V*G , V*D), sviluppando la funzione
sopra riportata in serie di Taylor nell’intorno di tale punto, si può esprimere una variazione
della corrente di drain in funzione delle corrispondenti variazioni della VG e della VD :
(
)
I D* + dI D = I D* VG* ,VD* +
∂I D
×
∂VG V =cos t .
D
dVG +
∂I D
×
∂VD V =cos t .
G
dVD
nella quale sono stati trascurati i termini contenenti derivate di ordine superiore al primo,
avendo supposto piccole le variazioni imposte. Derivando l'espressione analitica della ID
rispetto a VG e considerando VD = cost. , si ottiene il parametro “transconduttanza” gm :
1

∂I D
I P  Φi − VG + VD  2  Φi − VG
 - 

=
gm =
∂VG V = cost VP 
VP

 VP
D

1 
 2

 

valida nella zona lineare di funzionamento del JFET fino al limite della saturazione.
Particolarizzando questa espressione al caso limite VD = VDsat = VP + VG - Φi
si ottiene la
gm relativa alla zona di saturazione (gmsat):
g msat

 Φ − VG
IP 
1 -  i
=
VP 
 VP

1 
 2

 

La curva (a) di Fig. 5.11 rappresenta l’andamento teorico di gm in zona di saturazione,
normalizzato al rapporto IP / VP , in funzione della tensione di gate normalizzata. Si può
osservare come la transconduttanza si annulli quando si giunge in condizioni di
strozzamento, cioè per Φi - VG = VP . Il massimo valore di transconduttanza si dovrebbe
invece ottenere per VG = Φi , valore per il quale si ha la scomparsa della zona di
svuotamento. Tale condizione di forte polarizzazione diretta, come è ben noto dalla teoria sui
diodi a semiconduttore, non è fisicamente realizzabile. La curva (b) di Fig. 5.11 rappresenta
invece l’andamento della transconduttanza che si può rilevare su dispositivi reali:
V . 18
all’aumentare del valore di VG , poiché si ha un aumento della corrente di drain ID , gli effetti
delle resistenze delle zone neutre di source e drain non sono più trascurabili e la
transconduttanza assume valori inferiori a quelli teorici.
( gm VP ) / IP
1
(a)
0,5
(b)
0
0,2
0,4
0,6
0,8
1
(Φi – VG ) / VP
Fig. 5.11 – Andamento normalizzato della transconduttanza nella zona di saturazione in
funzione della tensione di gate normalizzata: (a) curva teorica; (b) curva sperimentale.
Nella Fig. 5.12.a è illustrato un modello semplificato del JFET per piccolo segnale. Tale
modello presenta in uscita un circuito equivalente di Norton, con un generatore di corrente
pilotato la cui intensità è proporzionale, tramite il fattore gm, alla tensione tra gate e source.
La “conduttanza di uscita” go , pari a :
go =
∂I D
1
=
∂VD V = cost rd
G
e posta in parallelo al generatore pilotato, rappresenta la pendenza delle caratteristiche di
uscita. Essa esiste ed è dovuta al fenomeno della modulazione della lunghezza del canale,
cioè al fatto che ID cresce leggermente, al crescere di VD oltre la VDsat , perché la lunghezza
della strozzatura del canale aumenta riducendo la lunghezza del canale. Infatti il termine IDSS
è inversamente proporzionale alla lunghezza del canale L. Pertanto il modello dinamico del
JFET è descritto dall’equazione iD = gmvG + govD.
Assumendo che attraverso la giunzione di gate polarizzata inversamente non scorre
corrente, si ha che la resistenza di ingresso rGS tra il gate e il source ha un valore infinito. Per
V . 19
lo stesso motivo anche la resistenza rGD tra il gate e il drain si suppone infinita. Le due
resistenze non vengono allora indicate nei modelli di Fig. 5.12.
G
D
go
gm vG
vG
a)
S
gm
rd = 1/go
0,01 - 1 MΩ
CDS
0,1 - 1 pF
CGS, CGD
1 - 10 pF
rGS, rGD
> 108 Ω
rS , rD
1 - 10 Ω
vD
S
0,1 - 10 mA/V
CGD
rD
G
D
go
b)
vG
CGS
gm vG
CDS
vD
rS
S
Fig. 5.12 – Modelli per piccolo segnale di un JFET: (a) schema semplificato valido a basse
frequenze; (b) modello completo valido anche ad alte frequenze. Essendo modelli dinamici, le
tensioni vG e vD rappresentano le variazioni dei valori statici (VG e VD) e sono pertanto indicate
con caratteri minuscoli. In tabella sono riportati i valori tipici dei parametri considerati.
Con riferimento alle trasformazioni che è possibile effettuare su circuiti lineari, per il
JFET è possibile considerare un modello per piccolo segnale in cui compare un circuito
equivalente di Thevenin, comprendente un generatore di tensione pilotato posto in serie ad
un resistore il cui valore rd è ottenuto in base alla definizione sopra riportata. La tensione del
generatore è legata alla tensione tra gate e source tramite un “fattore di amplificazione” µ
definito come:
µ=
∂VD
∂VG I = cost
D
Si dimostra che è valida la relazione µ = gm rd = gm / go
V . 20
In Fig. 5.12.b è riportato un modello per il JFET che risulta valido fino alle alte frequenze.
A differenza del modello valido per basse frequenze, in questo caso gli effetti delle tre
capacità interelettrodiche non sono più trascurabili. In figura vengono pure riportate le due
resistenze rS ed rD che tengono conto delle zone neutre presenti rispettivamente in
prossimità del source e del drain.
Considerando lo schema equivalente del JFET alle alte frequenze, si definisce come
massima frequenza di lavoro la “frequenza di taglio” fT , per la quale la corrente d’ingresso
del dispositivo è uguale alla corrente di drain quando questo elettrodo è cortocircuitato sul
source. Trascurando le due resistenze in serie rS ed rD , la corrente di ingresso si può
esprimere come:
i in = ω [C GS + C GD ] v g = 2 π f [C GS + C GD ] v g
La corrente di uscita in condizioni di cortocircuito vale, con piccole approssimazioni:
i out = g m v g
Di conseguenza, la frequenza alla quale le due correnti sono eguali è data da:
fT =
gm
2 π (C GS + C GD
)
Dall’espressione di gm ottenuta in precedenza, si ricava che il valore massimo teorico che
tale parametro può assumere è pari a IP / VP . Inoltre, con riferimento alla struttura planare di
Fig. 5.2 e supponendo un canale completamente svuotato di spessore 2a, si può impiegare
la seguente relazione per esprimere le due capacità di gate:
CGS + CGD = ε S
LZ
2a
Semplificando l’espressione di IP / VP si ottiene:
IP
=
VP
Z µ n q 2 N D2 a 3
εS L
q ND a
2
=
2 Z µ n q ND a
L
2εS
e pertanto:
fT =
2 Z µ n q ND a 2 µ n q ND a 2
=
εS L Z
π L2 ε S
2π L
2a
dalla quale si vede che per avere un JFET che raggiunga alte frequenze di lavoro, è
necessario che la lunghezza L del canale sia piccola (canale corto) e che il materiale abbia
µn elevata, come nel caso dell’arseniuro di gallio (GaAs).
V . 21
5.9. Dispositivi MESFET.
La struttura in sezione di un MESFET “a canale n”, realizzato in tecnologia planare, è
rappresentata in Fig. 5.13. Come si può notare, tale struttura è molto simile a quella del
JFET. La principale differenza consiste nel fatto che la giunzione di gate non è più di tipo p-n
ma è una giunzione metallo-semiconduttore (giunzione Schottky).
Gate (VG)
Source (VS)
n+
zona di
svuotamento
Drain (VD)
n+
c a n a l e
strato epitassiale
di tipo n
substrato semi-isolante
Fig. 5.13 - Sezione di un MESFET a canale n in assenza di polarizzazione
La tecnologia MESFET, sviluppata a partire dal 1966, viene comunemente impiegata per
la realizzazione di dispositivi ad effetto di campo su materiali semiconduttori realizzati con
elementi appartenenti ai gruppi III - V, quali GaAs, InP e loro composti. Tali materiali
risultano interessanti per la realizzazione di dispositivi in quanto caratterizzati da valori di
mobilità elettronica notevolmente superiori a quelli del Si. Tuttavia, a causa della difficoltà nel
produrre dei composti isolanti basati su tali materiali, da un punto di vista tecnologico è
difficile realizzare su di essi delle interfacce isolante-semiconduttore della qualità necessaria
al funzionamento di un dispositivo FET. Possono essere invece ottenute delle giunzioni
Schottky di elevata qualità.
Un altro vantaggio derivante dall'impiego di semiconduttori III - V è la disponibilità di
substrati cosiddetti "semi-isolanti", sui quali accrescere epitassialmente lo strato ad alta
mobilità che costituisce il canale. Tali substrati vengono realizzati drogando il materiale con
impurità (ad es. ferro) che generano dei livelli localizzati al centro della banda proibita. In tale
modo il livello di Fermi EF resta bloccato (pinned) in prossimità del livello intrinseco Ei e la
concentrazione dei portatori liberi, sia p sia n, è paragonabile a ni, facendo sì che la
resistività del materiale raggiunga valori elevatissimi. Ne consegue che gli effetti delle
capacità presenti tra substrato ed elettrodi e tra substrato e canale risultano minimizzati (le
capacità risultano collegate in serie tra loro tramite delle resistenze di valore elevatissimo).
Una ulteriore possibilità consiste nel realizzare dispositivi ad "eterogiunzione", così detti
perché la struttura impiegata è costituita da un certo numero di strati di semiconduttori
diversi, composti sempre con elementi appartenenti ai gruppi III - V. In tal modo è possibile
V . 22
scegliere opportunamente il materiale che costituisce il canale, che deve avere elevata
mobilità, ottenendo anche degli effetti di confinamento dei portatori, sfruttando le diverse
ampiezze della banda proibita nei diversi materiali. A questa famiglia di dispositivi
appartengono ad esempio gli HEMT (High Electron Mobility Transistors).
Si vuol infine far notare che, basandosi sull'opportuna scelta dei materiali e sullo
spessore del canale, oltre ai dispositivi a canale normalmente aperto (in cui, come per i
JFET, a VG = 0 è presente un canale conduttore), sono possibili dei dispositivi a canale
normalmente svuotato. In tali dispositivi il canale risulta strozzato già con tensione di gate
nulla. Il loro funzionamento avverrà allora rendendo positiva la tensione di gate (nel caso di
canale n), pur mantenendola al di sotto della tensione di soglia Vγ della giunzione.
Per ogni altro aspetto dei dispositivi MESFET, ed in particolare per le reti di
polarizzazione, resta valido quanto già detto a proposito dei JFET.
5.10. - Sistemi M.O.S.
La struttura fisica del MOSFET è quella riportata in Fig. 5.14. Come si può notare, è
simile a quella del JFET e differisce soltanto per le modalità con cui si effettua l’azione di
controllo tramite il terminale di gate, come detto all’inizio del capitolo.
Gate (VG)
SiO2
Source (VS)
Drain (VD)
y
x
n+
n+
L
substrato (bulk) di tipo p
Bulk (VB)
Fig. 5.14 – Sezione della struttura base di un dispositivo NMOS.
Poiché tale azione di controllo viene effettuata da una struttura che non abbiamo ancora
incontrato, cioè una struttura con tre materiali (Metallo-Ossido-Semiconduttore), è opportuno,
al fine di comprenderne il funzionamento, richiamare i diagrammi a bande di energia dei tre
materiali presi singolarmente, come riportato in Fig. 5.15.
V . 23
E0
E0
EC
qχ
E0
q χs
q Φm
q Φs
EC
EF
Eg=8eV
EF
EV
metallo
silicio (tipo p)
EV
SiO2
Fig. 5.145 - Diagramma a bande per l'alluminio, il biossido ed il silicio.
I sistemi MOS (Metal-Oxide-Semiconductor), cui appartengono i dispositivi MOSFET che
verranno descritti in seguito, hanno un ruolo fondamentale nella moderna tecnologia
microelettronica. La comprensione del loro funzionamento ha reso possibile il miglioramento
della progettazione dei circuiti integrati, delle loro prestazioni e soprattutto il raggiungimento
dell'integrazione a larghissima scala (VLSI, Very Large Scale of Integration).
I materiali comunemente impiegati nella tecnologia MOS sono l'alluminio (metallo), il
biossido di silicio (dielettrico) ed il silicio (semiconduttore). In tempi recenti l’alluminio è stato
quasi completamente sostituito da polisilicio ad alto drogaggio.
Per l'alluminio il lavoro di estrazione qΦm vale 4,1 eV. Per il silicio drogato p un valore
tipico di qΦs è 5 eV. L’affinità elettronica qχs per il silicio è di 4,15 eV, mentre per l'SiO2
qχ vale 0,95 eV.
Si consideri adesso cosa succede in seguito alla formazione del sistema MOS, ottenuto
accostando idealmente i tre materiali. Per poter giungere ad un modello sufficientemente
semplice del diagramma a bande della struttura MOS, è conveniente assumere le seguenti
ipotesi semplificative:
a)
E0 è una funzione continua del punto;
b)
la struttura del reticolo cristallino non viene alterata dalle discontinuità, per cui non sono
presenti stati energetici localizzati alle interfacce e possono adottarsi i diagrammi a
bande validi all’interno dei materiali;
c)
anche se il biossido di silicio (ottenuto per ossidazione termica esponendo la faccia della
fetta di Si ad un flusso di O2 in ambiente ad alta temperatura) è allo stato amorfo, si
assume valido per esso il diagramma a bande relativo al SiO2 cristallino.
V . 24
All’equilibrio il livello di Fermi tenderà ad allinearsi in tutto il sistema, con il trasferimento di
elettroni dal materiale con minor valore del lavoro di estrazione a quello con il maggiore e più
precisamente, in questo caso, dal metallo (M) al semiconduttore (S). Dato che è impossibile
che tale trasferimento avvenga attraverso l'SiO2 (ottimo isolante), ne consegue che le
condizioni di equilibrio si possono raggiungere solo se M ed S sono collegati elettricamente
dall’esterno, come in Fig. 5.16.
cariche fisse
+
+
+
+
+
-
p
M
O
S
(Al)
(SiO2)
(Si)
Fig. 5.16 - Sistema MOS in condizioni di cortocircuito
Dopo l'iniziale passaggio di elettroni dal metallo al semiconduttore, all’equilibrio nel
metallo si formerà, in prossimità dell’interfaccia M/SiO2, uno strato superficiale di cariche
positive (all’interno il metallo è equipotenziale). Di conseguenza nel semiconduttore si avrà la
formazione, in prossimità dell'interfaccia SiO2/Si, di una zona svuotata in cui sono presenti
un egual numero di cariche fisse negative. Tali cariche sono costituite da ioni accettori NA
non più saturati da altrettante lacune, essendosi queste ricombinate nel semiconduttore con
gli elettroni provenienti dal metallo in prossimità del contatto esterno.
In tali condizioni lo strato di SiO2, al cui interno non è presente alcuna carica mobile,
sostiene una caduta di potenziale V=Q/COX , dove con COX si è indicata la capacità dello
strato di dielettrico SiO2 di spessore dOX . Tale caduta ha un valore tipico pari a 0,6 V, che è
una parte del salto di potenziale Φm - Φs = 0,9 V dovuto ai differenti lavori di estrazione del
metallo e del semiconduttore prescelti. I restanti 0,3 V si ritroveranno nel semiconduttore e
precisamente ai capi della zona svuotata di cariche mobili affacciata al SiO2. E' quindi
possibile tracciare, nelle ipotesi assunte, il diagramma a bande del sistema MOS in assenza
di polarizzazione esterna (Fig. 5.17). Come si può notare, il diagramma a bande è simile a
quello incontrato nelle giunzioni M-S. Tuttavia, in questo caso, la presenza dell’ossido causa
una diminuzione del campo elettrico nel semiconduttore, in quanto è aumentata la distanza
tra le cariche superficiali. Inoltre, mentre nelle giunzioni M-S gli elettroni possono passare
attraverso la giunzione, nei sistemi MOS l’isolante non permette lo scorrimento degli elettroni
V . 25
attraverso il sistema. Le barriere che gli elettroni incontrano nelle due direzioni sono
rispettivamente di 3,15 eV (M → S) e 3,2 eV (S → M).
zona
svuotata
E0
E0
0,3eV
0,6eV
3,2eV
EC
3,15eV
EF
EV
EF
silicio (tipo p)
metallo
SiO2
dox
Fig. 5.17 - Diagramma a bande del sistema MOS in assenza di polarizzazione.
5.11. - Sistema MOS in presenza di polarizzazione esterna.
Come si è visto in Fig. 5.17, il sistema MOS forma un condensatore le cui armature sono
costituite una dal metallo e l'altra dal semiconduttore, separate dallo strato dielettrico di SiO2.
Tale condensatore, che tiene conto delle due capacità in serie, COX e C∆ (capacità di
barriera), è carico ad una tensione pari alla differenza, divisa per q, tra i lavori di estrazione
qΦm e qΦs divisa per q.
Se si applica una tensione dall’esterno il sistema non è più in equilibrio, per cui i livelli di
Fermi in M ed S si disallineano. Nel caso esaminato, se si applica una differenza di
potenziale con il segno negativo su M ed il segno positivo su S, tale tensione contrasta
quella che nasce all’equilibrio per effetto della differenza dei lavori di estrazione. In questo
modo si riduce la carica scoperta presente nel semiconduttore in condizioni di equilibrio.
Esiste un particolare valore VFB (flat band) che compensa esattamente la differenza
Φm - Φs. Con la scelta dei materiali effettuata, VFB vale 0.9 V con il polo negativo su M
(Fig. 5.18). In tal caso non c’è carica immagazzinata nel condensatore e quindi non c’è
campo elettrico al suo interno; in queste condizioni il diagramma a bande è piatto.
Ovviamente VFB dipende, a parità di coppia M-S, soltanto dal drogaggio del semiconduttore.
V . 26
E0
E0
3,15eV
3,2eV
p
EC
EF
M
SiO2
0,9eV
EF
EV
S
metallo
silicio (p)
0,9 V
SiO2
Fig. 5.18 - Sistema MOS in condizioni di bande piatte.
Continuando ad aumentare la differenza di potenziale (con il - su M), per |V|> VFB gli
estremi delle bande di energia nel silicio si abbassano ulteriormente e nel diagramma si
genera una concavità verso l'alto (Fig. 5.19). Infatti il condensatore MOS inizierà ad
immagazzinare carica positiva alla superficie del silicio. Tale carica è costituita da un
aumento di concentrazione delle lacune che vengono generate in questa zona per effetto
termico (gli elettroni sono subito allontanati dalla presenza del campo elettrico, per cui la
probabilità di ricombinazione è bassa). In queste condizioni, la superficie del semiconduttore
ha una densità di lacune p superiore a NA; questa condizione è detta “di accumulazione
superficiale” e lo spessore del semiconduttore che contiene l’aumento di lacune è detto
“strato di accumulazione”.
-
M
E0
E0
EF
EC
++
++
++
++
++
SiO2
S
qV
metallo
EF
EV
strato di
accumulazione
(lacune)
V > 0,9 V
silicio (tipo p)
SiO2
Fig. 5.19 - Sistema MOS in condizioni di accumulazione superficiale.
Poiché la regione di accumulazione è una regione di carica spaziale composta da
portatori liberi, l’equazione di Poisson può essere risolta in maniera analoga a quanto già
V . 27
visto per i contatti ohmici di tipo Schottky. Anche in questo caso è possibile collegare la
lunghezza di Debye LD allo spessore dello strato di accumulazione. Ad esempio, imponendo
p = 10 NA si ottiene un valore tipico per LD di circa 400 Å. Si ricordi che metà della carica
spaziale dovuta ai portatori liberi è contenuta entro
2 volte la lunghezza di Debye a partire
dalla superficie di separazione tra SiO2 e Si.
5.12. - Condizioni di svuotamento e di arricchimento con inversione.
Si è visto che con tensione nulla applicata dall'esterno tra M ed S, il MOS immagazzina
una carica negativa sulla superficie del Si affacciata all’SiO2 e carica positiva sulla superficie
del metallo. Questo fenomeno è spiegato dalla presenza di una tensione positiva interna tra
metallo e semiconduttore dovuta ai differenti valori del lavoro di estrazione.
Applicando dall’esterno una tensione con il positivo su M ed il negativo su S, la tensione
positiva complessiva ai capi del condensatore MOS aumenta. Cresce la carica positiva sul
metallo e quella negativa nel semiconduttore, quest’ultima in prossimità della interfaccia con
l'SiO2, si svuota sempre di più di cariche maggioritarie. Cresce quindi lo spessore xp della
zona di svuotamento.
Continuando ad aumentare in modulo la tensione applicata, il campo alla interfaccia
ossido-semiconduttore cresce; lo strato di semiconduttore, già svuotato delle cariche
maggioritarie in prossimità dell'interfaccia con l'ossido, si popola in tale zona di elettroni
generati termicamente ovvero richiamati dalle zone di source e di drain dal potenziale
positivo dello strato di SiO2 affacciato al semiconduttore. In tal caso, l'equilibrio all'interno del
silicio comporta che il livello di Fermi EF intersechi il livello intrinseco Ei e si avvicini ad EC,
creando uno "strato invertito" di cariche mobili, cioè arricchito di elettroni liberi (Fig. 5.20). Lo
strato invertito, creato dalla tensione, è detto così in quanto contiene più elettroni che lacune
ed è posto in una zona di semiconduttore drogato con atomi accettori. La conseguenza
dell'inversione è la creazione di una giunzione n-p all'interno del semiconduttore, posta in
prossimità dell'interfaccia con il SiO2.
Riassumendo, anche se il comportamento del sistema MOS è quello di un condensatore
(non lineare), le varie forme in cui può trovarsi lo strato di semiconduttore a contatto con
l'ossido, al variare della tensione applicata tra M ed S, influenzano molto le caratteristiche
elettriche di questo strato. Nella condizione di accumulazione, lo strato di semiconduttore è
ad alta conducibilità di tipo p ed è connesso elettricamente con il substrato sottostante. Nella
condizione di svuotamento, lo strato praticamente non conduce. Nella condizione di
arricchimento con inversione, esso è nuovamente ad alta conducibilità (di tipo n), ma isolato
elettricamente dal sottostante substrato.
V . 28
zona
svuotata
strato a conducibilità di tipo n (cariche mobili)
regione di svuotamento (ioni fissi NA )
+
+
+
+
+
+
+
M
-
SiO2
E0
E0
-
S
strato di
inversione
(elettroni)
EF
V
qV
EC
Ei
EF
EV
metallo
silicio (tipo p)
SiO2
Fig. 5.20 - Sistema MOS in condizioni di inversione.
Misure della capacità presentata dalla struttura MOS, per piccoli segnali ed al variare
della polarizzazione, fanno luce sui tre tipi di funzionamento descritti.
5.13. - Dispositivi MOSFET.
I dispositivi MOSFET (Metal-Oxide-Semiconductor Field Effect Transistor) sono spesso
chiamati IGFET (Insulated Gate FET), per distinguerli dai JFET (Junction FET). L'idea alla
base del MOSFET è nata prima (≅ 1932) del transistore bipolare, ma è stata realizzata per la
prima volta solo nel 1960 per difficoltà tecnologiche relative alla fabbricazione di interfacce di
alta qualità.
I simboli circuitali dei dispositivi MOSFET, per i due tipi a canale n e p, sono riportati in
Fig. 5.21. In essi è presente un quarto elettrodo B connesso al substrato (bulk). Dal
drogaggio di quest’ultimo dipende l’orientamento della freccia posta sull’elettrodo.
D
G
D
B
G
S
MOSFET a canale p (PMOS)
B
S
MOSFET a canale n (NMOS)
Fig. 5.21 - Simboli circuitali dei dispositivi MOSFET.
V . 29
La struttura base per un dispositivo NMOS planare è stata già riportata in sezione in
Fig. 5.14. Le regioni n+ di source e di drain, realizzate per diffusione o per impiantazione
ionica nel substrato di tipo p, risultano elettricamente isolate tra di loro, a meno che non si
crei una situazione di inversione nello strato di materiale di tipo p al di sotto del contatto di
gate. In tal caso si ottiene un canale indotto di tipo n tra source e drain, la cui conducibilità
dipende della tensione tra gate e substrato. La distanza L tra le regioni di source e di drain
lungo la direzione y viene detta "lunghezza del canale" ed è in genere dell'ordine del micron
(oggi inferiore al micron). La "larghezza del canale" Z, nella direzione ortogonale al foglio,
viene scelta in modo da avere una data conduttanza. Lo spessore dello strato di SiO2 è
dell'ordine di 100 nm. Poiché il dispositivo è simmetrico, si può distinguere il terminale di
source da quello di drain soltanto in presenza di corrente.
Se, con una opportuna scelta dei materiali e dei drogaggi, la condizione di inversione è
raggiunta con tensione nulla tra gate e bulk, il MOSFET è del tipo cosiddetto a svuotamento
(depletion), nel senso che per controllare la conducibilità del canale il MOSFET viene
polarizzato in modo da passare da una condizione di inversione ad una di svuotamento del
canale stesso. Nella maggior parte dei casi di impiego dei dispositivi MOSFET nei circuiti
integrati è invece necessario applicare una opportuna tensione tra gate e bulk (tensione di
soglia) per indurre una condizione di inversione, formando così un canale di tipo n nel
semiconduttore; in tal caso il MOSFET è del tipo ad arricchimento con inversione
(enhancement). Ci occuperemo più in dettaglio di questo ultimo tipo che è appunto il più
usato.
Si noti che, in entrambi i casi, il canale indotto è totalmente isolato dal substrato, a causa
della presenza della zona svuotata. Non occorrono quindi diffusioni di isolamento per
separare elettricamente tra di loro i vari dispositivi, il che consente di avvicinarli e di
realizzare un elevato numero di dispositivi per unità di superficie.
Si osservi infine che la principale differenza strutturale tra un dispositivo JFET ed uno
MOSFET consiste nel fatto che nel primo il canale tra source e drain è sempre fisicamente
presente grazie alla particolare struttura del dispositivo; nel secondo invece il canale viene
indotto dalla applicazione di una tensione all'elettrodo di gate.
5.14. Caratteristica ID - VD del MOSFET.
Come indicato nel disegno relativo alla sezione della sua struttura base (Fig. 5.14), il
MOSFET è un dispositivo a 4 terminali, per cui è possibile imporre indipendentemente l'una
dall'altra le tensioni applicate tra i vari terminali. Tuttavia, nella maggior parte delle
applicazioni, i terminali di source e di substrato (bulk) sono collegati assieme e posti ad un
potenziale di riferimento che può essere il potenziale di massa (VS = VB = 0). Per il corretto
V . 30
funzionamento del MOSFET a canale n, il substrato deve formare con le regioni di source e
di drain delle giunzioni polarizzate inversamente. Il drain viene polarizzato positivamente
rispetto al source (VD > 0), in modo che la giunzione substrato-drain risulti fortemente
polarizzata inversamente. Nel caso della giunzione substrato-source, una tensione di
polarizzazione
nulla
rappresenta
una
condizione
limite
di
polarizzazione
inversa
perfettamente tollerabile, essendo comunque nulla la corrente che percorre tale giunzione.
Come accennato in precedenza, il funzionamento del MOSFET si basa sulla capacità di
indurre una condizione di inversione al di sotto del gate. Un'analisi dettagliata sulla struttura
MOS mostra che, affinché si verifichi l'inizio di una forte inversione (condizione definita da
ns = NA , dove ns è la concentrazione di carica indotta nella zona di inversione) è necessario
che VG raggiunga un certo valore VT, detta "tensione di soglia", il cui valore dipende da vari
contributi; tra questi vi sono sicuramente VFB, VD (tensione di drain), l'incurvamento delle
bande e la tensione che cade nella zona svuotata di cariche mobili. Tale valore varia tra 0,5V
ed 1,5V per gli NMOS, tra -0,5V e -1,5V per i PMOS.
Si supponga, come nel JFET, che VD sia molto piccola, cosicché la carica nel canale non
vari sensibilmente con la tensione applicata tra gli elettrodi di source e drain. Se VG > VT , si
hanno le situazioni rappresentate nelle sezioni del dispositivo riportate in Fig. 5.22.
VG
Source
Source
VG
VD
n+
n+
VD
n+
n+
p
p
Bulk
zona invertita
a)
Bulk
zona svuotata
VD = 0
b)
0 < VD < VG - VT
Fig. 5.22 - Dispositivo NMOS in cui è applicata una VG > VT.
Nel caso di Fig. 5.22.a, in cui VD = 0, la regione di inversione e quella di svuotamento
hanno ampiezza uniforme lungo y. Nel caso di Fig. 5.22.b, in cui
0 < VD < VG - VT ,
l'allargamento della zona svuotata ed il restringimento del canale sono dovuti agli effetti del
potenziale positivo del drain, che si oppone all’inversione.
Per ricavare quantitativamente una relazione che leghi la corrente di drain ID alla
tensione di gate VG, indichiamo con Qn la carica dovuta agli elettroni indotti nello strato di
inversione; la corrente ID tra drain e source vale:
V . 31
ID = - Qn / Ttr
ove Ttr è il tempo di transito degli elettroni, cioè il tempo impiegato dagli elettroni per andare
dal source al drain. Dato che la corrente è trasportata per drift (campo elettrico) e non per
diffusione, Ttr sarà pari alla lunghezza del canale L diviso per la velocità di drift degli elettroni
vdrift, che vale, con buona approssimazione:
vdrift = - µn E = µn VD / L
Si ottiene allora:
Ttr =
L
v drift
=
L2
µ nVD
Si noti che il valore di µn da considerare nella formula di sopra è circa il 50 % del valore tipico
di µn , a causa della presenza, in prossimità della superficie, di una elevata densità di difetti
reticolari. Si dimostra che la carica indotta è:
Qn = − COX (VG − VT )
cioè la concentrazione di elettroni nello strato di inversione varia linearmente con la
differenza tra la tensione VG e la tensione di soglia VT. Nella formula, COX rappresenta la
capacità offerta dallo strato di biossido di silicio, che vale evidentemente:
COX = εOX
LZ
dOX
essendo dOX lo spessore dello strato (che nei casi più comuni varia tra i 10 e 100 nm),
L Z l'area della struttura MOS e εOX la costante dielettrica del biossido di silicio
(34,53·10–14 F/cm). Combinando le formule sopra riportate, è possibile ricavare
un'espressione di ID in funzione delle tensioni applicate al MOSFET, valida per bassi valori di
ID:
ID =
COX (VG -VT )
L2
µ nVD = εOX
Z µn
(VG -VT ) VD
L dOX
quindi, a basse correnti, ID risulta proporzionale a VD, essendo la costante di proporzionalità
data dalla conduttanza GD pari a:
GD = εOX
Z µn
(VG -VT )
L dOX
che dipende, come si è già visto nel JFET, dalla tensione di gate VG.
All'aumentare di VD non è più lecito trascurare la sua influenza sul valore di VT. Si può
intuire che un aumento di VD contrasta la condizione di inversione nella zona del canale
prossima al terminale di drain e causa invece un allargamento dello strato di svuotamento tra
canale e bulk. La VG quindi non è più in grado di mantenere lo strato di inversione vicino al
V . 32
drain ed il canale si strozza, analogamente a quanto già visto nel JFET. In tali condizioni di
VD elevata, che si abbinano al passaggio di una ID non più trascurabile, si ha un
accorciamento della lunghezza del canale L che si riduce ad L' (Fig. 5.23).
VG
Source
VD
n+
n+
L'
p
L
Bulk
Fig. 5.23 - Dispositivo NMOS in condizioni di saturazione.
Un'analisi approssimata può farsi assumendo che tra l'elettrodo gate ed il canale vi sia
una differenza di potenziale media applicata pari a VG – VD / 2. Allora l'espressione della
carica Qn può essere riscritta come:
Qn = − COX (VG − VD /2 − VT )
e la corrente ID diventa:
I D = εOX
Z µn
Z µn
(VG -VD /2 - VT ) VD = εOX
[2(VG -VT )VD - VD2 ]
L dOX
L dOX
VDsat
ID
VG-VT = 6 V
20 mA
5V
4V
10 mA
3V
2V
1V
0
4V
20V
Fig. 5.24 - Caratteristiche di uscita di un NMOS ad arricchimento.
VD
V . 33
Le caratteristiche di uscita (curve a VG = cost.), riportate in Fig.23, sono delle rette
passanti per l'origine per valori di VD molto bassi, con pendenza data dall'espressione di GD.
Al crescere di VD esse assumono invece l'andamento parabolico descritto dalla espressione
di ID sopra riportata, valida per correnti non trascurabili.
Per VD = VG - VT si ha lo strozzamento del canale (condizione di saturazione) e la
corrente rimane costante; contemporaneamente la parabola raggiunge il suo vertice. Per
VD > VG - VT l'espressione di ID sopra riportata non è più applicabile, in quanto essa
prevedrebbe una ∂ ID / ∂ VD negativa: si ha invece una riduzione della lunghezza del canale.
Per spiegare qualitativamente l'andamento delle caratteristiche in questa regione, si può
osservare che gli elettroni che si muovono nel canale invertito non vedono alcuna barriera a
mano a mano che si avvicinano alla zona di svuotamento in prossimità del drain; viceversa,
quando essi entrano nella zona di svuotamento vi trovano una regione interessata da un
elevato campo elettrico, per cui vengono accelerati. La corrente ID è quindi determinata dalla
velocità con cui gli elettroni incidono sul bordo della regione di svuotamento. Questa velocità
risulta, in prima approssimazione, indipendente da VD. La corrente ID diviene quindi costante,
ovvero "satura", per VD > VG - VT. Quindi i massimi delle caratteristiche si hanno in
corrispondenza di una tensione VDsat , oltre la quale le caratteristiche diventano delle rette
parallele all'asse delle ascisse. Riassumendo, si può ottenere il luogo dei punti sulle
caratteristiche a VG – VT = cost., corrispondenti all'inizio della saturazione, nonché le correnti
di saturazione, dati rispettivamente da:
VDsat = VG - VT
I Dsat = εOX
Z µn
(VG -VT )2
2 L dOX
Dai ragionamenti finora svolti si dovrebbe avere che la corrente di drain resti pari a ID sat
anche per valori di VD maggiori di VD sat. In realtà, al crescere di VD, diminuisce la lunghezza L
del canale che figura a denominatore dell’espressione di ID sat. Quindi quest’ultima corrente
cresce al crescere di VD. Di questo effetto si può tenere conto moltiplicando l’espressione di
V
ID sat per la quantità 1 + D

 , dove V viene chiamata “tensione di Early” e rappresenta
A
V A 
il valore di tensione VD intercettato dal prolungamento delle caratteristiche di saturazione
sull’asse delle ascisse.
Analogamente a quanto già osservato nel JFET, anche nel MOSFET si assiste, ad alti
valori della tensione di drain VD, ad un fenomeno di rottura, come testimoniato
dall'improvviso impennarsi delle curve caratteristiche di Fig. 5.24. Dalle stesse si osserva
però che la rottura si ha ad un prefissato valore di tensione VD e che tale tensione è
V . 34
indipendente dal valore di tensione di gate VG. Infatti, a differenza del JFET, dove la
massima tensione che si può applicare tra due terminali qualsiasi è la più bassa tensione
che provoca il breakdown a valanga della giunzione di gate, nel caso del MOSFET la rottura
si verifica alla giunzione tra il drain ed il substrato, polarizzata inversamente (il gate è isolato
da uno strato di ossido la cui tensione di perforazione è in genere di gran lunga superiore).
Quando si innesca la condizione di rottura, la corrente di source IS non varia visto che VD è
costante, ma aumenta notevolmente la corrente di drain ID che, in questo caso, scorre per lo
più attraverso il substrato ed esce dal suo terminale.
Per quanto riguarda il comportamento dinamico per piccoli segnali del MOSFET, si
possono usare degli schemi equivalenti uguali a quelli già visti per il JFET (Fig. 5.12).
Possono anche farsi analoghe considerazioni per quanto riguarda le semplificazioni
effettuabili. I valori di alcuni parametri differenziali nel MOSFET sono diversi da quelli del
JFET. In particolare: la transconduttanza gm raggiunge valori di 20 mA/V ed oltre; la
resistenza dinamica rd invece si riduce a valori di circa 1 - 50 kΩ; aumentano infine
notevolmente i valori di resistenza tra gate e source (rGS > 1010 Ω) e tra gate e drain
(rGD > 1014 Ω), ciò grazie alla presenza dello strato di ossido di gate.
5.15. Polarizzazione del MOSFET.
Le reti di polarizzazione per i MOSFET sono molto simili a quelle già esaminate per i
JFET. Inoltre continuano a valere tutte le considerazioni fatte in quella sede relativamente ai
criteri di scelta del punto di riposo, al suo posizionamento in zona di saturazione ed alle
ridotte problematiche di fuga termica. In particolare, nel caso dei MOSFET a svuotamento,
dati i versi delle tensioni in gioco e tenendo conto delle corrispondenti polarità dei dispositivi
(a canale n o p), esse sono del tutto identiche.
Qualche differenza presentano invece i circuiti di polarizzazione per MOSFET ad
arricchimento con inversione. Il tipo più semplice di circuito è riportato in Fig. 5.25.a. Il gate
viene polarizzato tramite la resistenza RG connessa verso il drain. Poiché la corrente di gate
è praticamente nulla, il gate risulta alla stessa tensione di drain (VG = VD). L’azione
stabilizzatrice nei confronti della ID è assicurata dalla resistenza RG ; infatti se la ID aumenta,
diminuisce la VD e quindi diminuisce della stessa quantità la VG , il che induce una riduzione
della ID . Applicando la legge di Kirchhoff alla maglia di uscita si ottiene l’espressione della
retta di carico:
E = VD + RD ID
V . 35
Dovendo procedere per via analitica, si può considerare l’espressione ricavata in precedenza
che forniva per il MOSFET i valori di ID in funzione di VD all’interno della regione di
saturazione:
I Dsat = εOX
Z µn
(VG -VT ) 2
2 L d OX
Imponendo in questa la condizione VG = VD e ponendola a sistema con l’equazione alla
maglia di uscita, è possibile ricavare il punto di riposo in termini di ID e VD .
E
ID
VDsat = VG - VT
E/RD
RG
VD = VG
RD
D
B
S
G
VD
V*G
I*D
VGS
a)
b)
V*D
E
VD
Fig. 5.25 – (a) Semplice circuito di polarizzazione per un MOSFET ad arricchimento a
canale n. (b) Caratteristiche di uscita del MOSFET con retta di carico e curva VD =VG.
Seguendo invece l’approccio grafico, è possibile determinare il punto di riposo con
qualche semplice considerazione. Come prima cosa si traccia sulle caratteristiche ID - VD la
retta di carico (Fig. 5.25.b). Si può poi notare che la condizione VG = VD è descritta sul piano
delle caratteristiche da una curva ottenuta traslando verso destra, di una quantità pari a VT ,
la curva che rappresenta la condizione di saturazione VD = VG - VT . Il punto di intersezione
tra la retta di carico e la curva per VG = VD identifica il punto di riposo del MOSFET
(I*D, V*G, V*D).
In Fig. 5.26.a è riportata una versione migliorata del circuito sopra considerato, nella
quale è possibile scegliere il valore della VG mediante il partitore RG - R . Poiché il gate non
assorbe corrente, la VG è data da:
VG = VD
R
R + RG
Scegliendo per RG ed R dei valori elevati (dell’ordine dei MΩ), il partitore praticamente non
assorbe corrente per cui si può ancora ritenere valida la:
V . 36
E = VD + RD ID
Sul piano delle caratteristiche l’intersezione tra la retta di carico e la curva che lega VG a VD
sarà posizionata più a destra che nel circuito precedente, essendo infatti VD > VG .
E
RG
R1
RD
D
B
S
G
R
E
VD
RD
D
B
S
G
VGS
VD
VGS
a)
b)
RS
Fig. 5.26 – (a) Versione migliorata del circuito di polarizzazione per MOSFET.
(b) Circuito di polarizzazione a quattro resistenze per MOSFET.
Infine in Fig. 5.26.b è riportata la rete di polarizzazione a quattro resistenze, che
consente una maggiore libertà nella scelta dei valori della tensione applicabile all’elettrodo di
controllo VG ed una migliore stabilizzazione nei confronti delle variazioni di ID . A differenza di
quanto visto nell'analogo circuito di polarizzazione dei JFET, lavorando con i MOSFET ad
arricchimento con inversione a canale n bisogna verificare che la tensione di gate risulti
positiva, il che si traduce nella condizione:
VG = E
R2
> I D RS
R1 + R 2
Inoltre, poiché in un circuito amplificatore il MOSFET deve lavorare nella zona di
saturazione, bisogna verificare che risulti:
VD > VG - VT
L'analisi del circuito si effettua considerando l'equazione alla maglia d'uscita (che
rappresenta la retta di carico):
E = VD + (RD + RS) ID
e quella alla maglia di ingresso:
E
R2
= VG + I D R S
R1 + R 2
V . 37
Si potrà quindi procedere con la risoluzione grafica utilizzando la curva di polarizzazione, o
con quella analitica impiegando l'espressione della ID in funzione della VD .
5.16. - La tecnologia C-MOS (Complementary MOS).
La tecnologia C-MOS rappresenta la tecnologia in assoluto più diffusa per la
realizzazione di dispositivi integrati digitali. L'unità base che si considera è costituita da un
semplice circuito invertitore logico, ottenuto a partire da una coppia di dispositivi PMOS e
NMOS opportunamente accoppiati. In particolare i due dispositivi hanno rispettivamente in
comune i due gate ed i due drain. Lo schema elettrico dell'invertitore è riportato in
Fig. 5.27.a, dove sono pure indicati i valori tipici per le tensioni di soglia VT
dei due
dispositivi.
Il funzionamento del circuito è molto semplice: se la tensione di ingresso Vin è nulla
(livello logico 0), la tensione gate-bulk dell'NMOS è al di sotto della tensione di soglia VTn,
per cui esso non conduce (Fig. 5.27.b). Per quanto riguarda il PMOS, invece, la tensione
negativa gate-bulk risulta pari a -VDD e quindi, in modulo, superiore alla VTp, Ciò significa che
il PMOS conduce e la tensione d'uscita Vout risulta pari a VDD (livello logico 1).
La situazione si inverte quando Vin viene portata a VDD (livello logico 1): l'NMOS passa in
conduzione (Fig. 5.27.c), mentre il PMOS è interdetto. Di conseguenza la Vout si porta a 0V
(livello logico 0).
VTp= - (0,5÷1) V
G
VDD
VDD
VDD
S
B
D
PMOS
Vout= VDD
Vin
Vout
G
VTn= (0,5÷1) V
a)
Vout= 0
D
B
S
NMOS
Vin= 0
Vin= VDD
VSS
b)
c)
Fig. 5.27 – (a) Schema elettrico di un circuito invertitore C-MOS. (b), (c) Modelli semplificati
dello stesso circuito nei due possibili stati di commutazione.
V . 38
Si vede così che, in entrambi gli stati stazionari, la corrente che fluisce attraverso il
circuito è virtualmente nulla, dato che i due canali sono in serie e che comunque uno dei due
dispositivi è all'interdizione. La corrente risulta diversa da zero durante la fase di
commutazione tra i due stati logici, tuttavia i tempi di commutazione sono abbastanza ridotti
(10 ÷ 100 nsec) per cui la potenza media dissipata è dell'ordine dei nW per ogni porta logica.
Una sezione estremamente semplificata relativa alla struttura di un C-MOS integrato è
riportata in Fig. 5.28. Si vuol far notare la presenza, nella struttura in esame, di uno strato
profondo di biossido di silicio posto sotto il contatto comune ai due drain. Tale strato è in
effetti costituito da una trincea, scavata per attacco chimico anisotropo in fase gassosa (dry-
etching), che viene in seguito riempita con biossido di silicio. La funzione della trincea è
quella di realizzare un isolamento tra le zone a vario drogaggio che costituiscono il
dispositivo NMOS e quelle che costituiscono il PMOS. La ragione di tale precauzione nasce
dall'osservazione che, procedendo ad esempio dal source dell'NMOS (zona di tipo n+),
passando dal suo canale (zona di tipo p), giungendo al substrato-canale del PMOS (zona di
tipo n) ed infine al source del PMOS (zona di tipo p+), si viene a realizzare un dispositivo p-n-
p-n parassita. Tale dispositivo può, sotto opportune condizioni, dare luogo ad un innesco
(latch-up) che causa il passaggio di una elevata corrente tra il source dell'NMOS e quello del
PMOS, dato che ai suoi capi è applicata una tensione complessiva pari a VDD-VSS, con la
possibile distruzione del circuito. Per evitare l'innesco è assolutamente necessario ridurre di
molto il guadagno dei due transistori che costituiscono il dispositivo p-n-p-n parassita. Un
modo per ottenere ciò è appunto quello di allungare il percorso che i portatori devono
effettuare per dar luogo all'effetto transistorico.
Vin
= SiO2
VDD
VSS
Vout
n+
p+
PMOS
p+
n+
NMOS
isola di tipo p
n+
substrato di tipo n
Fig. 5.28 - Sezione di un circuito invertitore C-MOS integrato.
p+
V . 39
Si noti infine che la diffusione di tipo n+ presente alla sinistra del contatto di source del
PMOS permette di collegare il substrato di tipo n (bulk) allo stesso terminale di source.
Analoga funzione svolge la diffusione p+ , presente alla destra del contatto di source
dell’NMOS, nei confronti dell’isola di tipo p (detta anche “vasca” o p-tub) che funge da
bulk per l’NMOS.
Una tipica applicazione di NMOS a circuiti logici è quella del circuito rappresentato in
Fig. 5.29 che espleta la funzione NOR (OR negato).
+VDD
RD
Vout
V1
V2
V1
V2
Vout
0
0
1
1
0
0
0
1
0
1
1
0
Fig. 5.29 – Applicazione di NMOS ai circuiti logici
Scegliendo RD >> RON degli NMOS, si ha che quando V1 e V2 sono nello stato “0”, gli
NMOS sono aperti e quindi VOUT = VDD, cioè allo stato “1”. Quando V1 o V2 o entrambi
sono nello stato alto, cioè maggiore di VT, gli NMOS si comportano da tasti chiusi e quindi
VOUT = 0.