1 Punti, segmenti, poligoni nel piano cartesiano: rigore e

Punti, segmenti, poligoni nel piano cartesiano: rigore e concretezza
di Luciano Porta
Ricordiamo che, nel piano, il riferimento cartesiano ortogonale è costituito da una retta orizzontale, l’asse
delle ascisse o asse X (orientato da sinistra verso destra) e da una retta verticale, l’asse delle ordinate o asse
Y (orientato dal basso verso l’alto). Gli assi si intersecano nell’ origine: il punto O ≡ (0;0). Il piano viene così
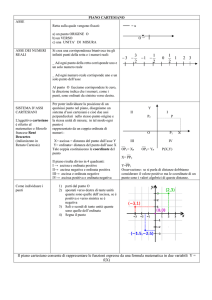
diviso in quattro quadranti: Il primo in alto a destra, il secondo in alto a sinistra, il terzo in basso a sinistra e
il quarto in basso a destra. La posizione di un punto sul piano è data dalle sue due coordinate: nell’ordine
l’ascissa è la distanza del punto dall’asse Y (si misura sull’asse X) e l’ordinata è la distanza del punto
dall’asse X (si misura sull’asse Y). In pratica il primo numero, l’ascissa, indica di muoverci orizzontalmente
sull’asse X (a sinistra se è negativa e a destra se è positiva) e il secondo numero, l’ordinata, dice di muoverci
verticalmente dal punto individuato dall’ascissa (in basso se è negativa e in alto se è positiva). A ogni punto
corrisponde una coppia ordinata di numeri relativi e possiamo applicare alla geometria il metodo algebrico.
Punti nel piano cartesiano
Segmenti nel piano cartesiano
Poiché la lezione è dedicata in particolar modo a studenti della scuola secondaria di primo grado, preferisco
che non sia utilizzata l’usuale formula per determinare la distanza tra due punti. Questa formula, spesso
dimostrata solo in casi particolari anche successivamente, è frequentemente origine di errori.
Possiamo farne a meno se determiniamo sul piano cartesiano solo la lunghezza dei segmenti orizzontali e
verticali. Calcoleremo successivamente la lunghezza dei segmenti obliqui applicando il teorema di Pitagora.
Nel proseguimento della lezione porremo 1 cm come unità di misura su entrambi gli assi cartesiani.
1) Segmenti orizzontali
Le ordinate degli estremi di un segmento orizzontale sono uguali. Per determinarne la lunghezza
utilizzeremo le ascisse degli estremi. Osserviamo le diverse situazioni mostrate nella figura seguente.
1
I segmenti AB e IL hanno le ascisse discordi ( i due segmenti attraversano l’asse Y).
I segmenti CD e GH hanno le ascisse concordi ( i due segmenti non attraversano l’asse Y).
Il segmento EF ha un estremo sull’asse Y. Conoscendo il significato e il simbolo di valore assoluto scriviamo:
AB = ( Ι-4 Ι + Ι 3 Ι ) cm = 7 cm
IL = ( Ι-2 Ι + І 6 І ) cm = 8 cm
CD = ( І-7 Ι – Ι-3 І ) cm = 4 cm
GH = ( І 7 І – І 2 І ) cm = 5 cm EF = ( І-5 І ± 0 ) cm = 5 cm
Se le ascisse sono concordi sommiamo i valori assoluti.
Se sono discordi sottraiamo dal valore assoluto maggiore quello minore.
2) Segmenti verticali
Le ascisse degli estremi di un segmento verticale sono uguali. Per determinarne la lunghezza utilizzeremo le
ordinate degli estremi. Osserviamo le diverse situazioni mostrate nella figura seguente.
I segmenti GH e CD hanno le ordinate discordi ( i due segmenti attraversano l’asse X).
I segmenti AB e IL hanno le ordinate concordi ( i due segmenti non attraversano l’asse X).
Il segmento EF ha un estremo sull’asse X. Conoscendo il significato e il simbolo di valore assoluto scriviamo:
GH = ( Ι 2 Ι + Ι-4 Ι ) cm = 6 cm
CD = ( Ι 3 Ι + І-2 І ) cm = 5 cm
IL = ( І-3 Ι – Ι-1 І ) cm = 2 cm
AB = ( І 5 І – І 2 І ) cm = 3 cm EF = ( І 4 І ± 0 ) cm = 4 cm
Se le ordinate sono concordi sommiamo i valori assoluti.
Se sono discordi sottraiamo dal valore assoluto maggiore quello minore.
2
3 ) Segmenti obliqui
Avendo determinato la lunghezza dei cateti (uno orizzontale e uno verticale) come negli esempi precedenti,
possiamo calcolare la lunghezza dell’ipotenusa per mezzo del teorema di Pitagora.
Come ricavare le coordinate di un punto da quelle di altri punti
Spesso nello studio dei poligoni sul piano cartesiano non conosciamo dal testo le coordinate di alcuni punti
essenziali per la risoluzione del problemi.
Possiamo però ricavare dai punti noti le coordinate di questi punti riflettendo sul significato di ascissa e
ordinata.
3
Determinazione di perimetro e area di poligoni nel piano cartesiano
1° esempio
Considerare i seguenti punti nel piano cartesiano:
A≡(-7;-3), B≡( 4;-3), C≡(-2; 5), D≡(-7; 5). Tracciare i segmenti AB, BC, CD, AD.
Se su entrambi gli assi cartesiani l’unità di misura è 1cm, determinare perimetro e area del poligono ABCD.
Risoluzione
AB=(І-7І+І 4І)cm=11cm CD=(І-7І-І-2І)cm=5cm AD=(І-3І+І 5І)cm=8cm
HB=AB-DC=(11-5)cm=6cm
BC= HB2+HC2 = 62+82cm= 36+64 cm= 100 cm=10cm
2P(ABCD)=AB+BC+CD+AD=(11+10+5+8)cm=34cm
A(ABCD)=(AB+CD)*AD/2=[(11+5)*8)/2]cm2=64cm2
----------------------------------------------------------------------------------------------------------------------------------------------2° esempio
Considerare i seguenti punti nel piano cartesiano:
A≡(-4; 1), B≡( 2; 1), C≡(-1; 5). Tracciare i segmenti AB, BC, AC.
Se su entrambi gli assi cartesiani l’unità di misura è 1cm, determinare perimetro e area del poligono ABC.
AB=(І-4І+І 2І)cm=6cm CH=(І 5І-І 1І)cm=4cm
HB=AB/2=(6/2)cm=3cm
BC= HB2+HC2 = 32+42cm= 9+16 cm= 25 cm=5cm
2P(ABC)=AB+2*BC=(6+2*5)cm=(6+10)cm=16cm
A(ABC)=AB*CH/2=(6*4/2)cm2=12cm2
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI UNO
4