Verifica di matematica
Polinomio
Grado
Numero
termini
Omogeneo
1. Semplifica le seguenti espressioni:
=
=
2 3 1 3 7 2
3 3 1 2 1 3 5 2 1 2
x x y y xy x y y x xy =
4
2
3 2
2
2
3
4
2. Sottrai dai
2
9
1
del polinomio x 2 x il doppio di x 2 x 6
3
2
3
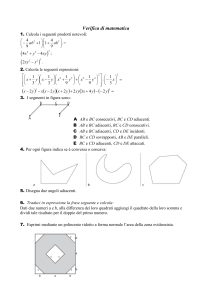
3. In figura 1 possiamo distinguere in totale:
a. 2 segmenti
b. 6 segmenti
c. 4 segmenti
d. 10 segmenti
e. 8 segmenti
4. In figura 1 le semirette:
a. AC e BC sono disgiunte
b. AB e BD hanno come intersezione il segmento AB
c. AB e CD hanno come intersezione il segmento CD privato degli estremi
d. BA e CD sono disgiunte
e. nessuna delle precedenti è vera
5. Guardando la figura 1 possiamo dire riguardo ai segmenti che:
a. AB e CD sono disgiunti
b. AB e BC sono disgiunti
c. AB e CD sono adiacenti perché giacciono sulla stessa retta
d. AC contiene BD
e. l’intersezione tra AC e BD è CD
Completo
rispetto a m
6. Completa in modo che l' uguaglianza sia vera:
2x b
.....
.... 3 2
64 x12b18
2 8 3
a b :
5
7. Guardando la figura 4 possiamo dire che:
a.
e sono adiacenti
b.
e sono consecutivi
c.
e sono adiacenti
d.
e sono opposti al vertice
e.
e sono consecutivi
8. Esprimi la misura dell’area grigia mediante un monomio:
5
= a 4b
2