Contare gli anagrammi di una parola

Contare gli anagrammi di una parola
Quanti sono gli anagrammi della parola CANE? Ed il numero di diverse file formate
da quattro persone? Il numero è lo stesso in entrambi i casi: è il numero di possibili
ordinamenti di quattro oggetti distinti. Si può immaginare ognuno di questi
ordinamenti come il risultato di un procedimento in quattro passi:
1. Si sceglie il 1° elemento: ciò è possibile in 4 modi diversi.
2. Si sceglie il 2° elemento: avendo già assegnato il primo elemento, ciò è possibile
in 3 modi diversi.
3. Si sceglie il 3° elemento: avendo già assegnato i primi due elementi, ciò è
possibile in 2 modi diversi.
4. Si sceglie il 4° elemento: avendo già assegnato i primi due elementi, ciò è
possibile in 1 modo soltanto.
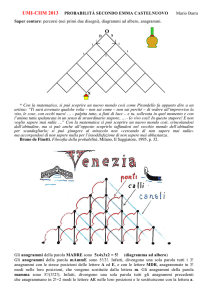
Questo procedimento può essere rappresentato da un diagramma ad albero. La figura
sottostante si riferisce all’anagramma. Supponendo, ad esempio, che la prima lettera
scelta sia la C, si procede come indicato dalle frecce. Il percorso evidenziato in rosso
corrisponde all’anagramma CENA:
1.
2.
3.
4.
N
E
E
N
A
E
E
A
A
N
N
A
A
C
N
E
Ad ognuna delle possibili 4 scelte della prima lettera corrispondono, come vediamo,
3 scelte per la seconda lettera, a ciascuna di queste ultime corrispondono 2 scelte per
la terza lettera, ed una sola scelta per l’ultima lettera rimasta. Dunque,
complessivamente, i possibili anagrammi sono:
4321 = 24
In generale:
Il numero di possibili ordinamenti (permutazioni o disposizioni senza ripetizione)
di n oggetti distinti è
n(n1)(n2)21 = n!
Il simbolo a secondo membro indica il prodotto dei numeri interi da 1 a n e si legge
“n fattoriale”. Calcoliamo i primi fattoriali:
1! = 1
2! = 21 = 2
3! = 321 = 6
4! = 4321 = 24
5! = 54321 = 120
6! = 654321 = 720
Inoltre si pone, per convenzione,
0!=1.
Nota Per indicare, in generale, una permutazione di 4 oggetti non ulteriormente
specificati, si ricorre ai numeri interi da 1 a 4, prendendo come sequenza di
riferimento 1 2 3 4. Ad esempio, se si fa corrispondere quest’ultima a CANE,
l’anagramma CENA si potrà rappresentare come la sequenza 1 4 3 2, ACNE come 2
1 3 4, NAEC come 3 2 4 1, e così via. In modo, analogo, utilizzando i numeri interi
da 1 a n, è possibile rappresentare le permutazioni di n oggetti distinti.
Generalizzazione
Il numero di anagrammi di una parola di n lettere è pari a n! solo se le sue lettere sono
tutte diverse. Il numero è invece inferiore in presenza di ripetizioni: ad esempio, gli
anagrammi della parola ASSO non sono 4! = 24, ma solo i seguenti 12:
ASSO, ASOS, AOSS, SASO, SAOS, SOAS, SOSA, SSAO, SSOA, OASS, OSAS,
OSSA.
Anche in questo caso, un opportuno ragionamento ci consente di determinarne a
priori il numero: basta tenere conto che l’uguaglianza tra lettere produce una
identificazione tra permutazioni formalmente distinte. Poiché in ASSO coincidono la
la 2a e la 3a lettera, sono identici gli anagrammi corrispondenti a:
1 2 3 4 e 1 3 2 4 (ASSO)
1 2 4 3 e 1 3 4 2 (ASOS)
e così via. In generale, sono da identificare le permutazioni che si ottengono una
dall’altra invertendo 2 e 3. Le permutazioni vengono così raggruppate 2 a 2, e ciò
spiega perché le permutazioni distinte sono, in tutto, 24/2 = 12. In altri termini,
occorre dividere il numero totale di permutazioni per il numero di permutazioni di
due elementi (2 e 3), cioè, appunto, per 2! = 2.
Analogamente, il numero degli anagrammi della parola SASSO, in cui tre lettere
sono uguali, si ottiene dividendo il numero delle permutazioni di cinque elementi per
il numero delle permutazioni di tre elementi: 5!/3! = 120/6 = 20.
Per determinare gli anagrammi della parola OSSO, possiamo immaginare di
identificare, negli anagrammi della parola ASSO, la 1 a e la 4a lettera. Ciò, come
abbiamo visto, significa dividere il numero di anagrammi di ASSO per 2: gli
anagrammi di OSSO sono dunque 24/4 = 6. In effetti sono i seguenti:
OSSO, OSOS, OOSS, SOSO, SOOS, SSOO.
In generale, è chiaro che
Il numero di possibili ordinamenti di n oggetti, che si identificano, separatamente, a
gruppi di k1, k2, ... , kn è
n!
k1! k2!  kn!
In base a questa formula, ad esempio, il numero di anagrammi della parola MAMMA
è
5! 120

 10.
2!3! 12
Sono, precisamente:
MAMMA, MAMAM, MAAMM, MMAMA, MMAAM, MMMAA, AAMMM,
AMAMM, AMMAM, AMMMA.